A formula for electron mass calculation based on new fundamental concepts

Yvan-Claude Raverdy

doi:10.37532/2752-8081.23.7(2).129-133

Yvan-Claude Raverdy^*

Independent Researcher, France, Email: ycraverdy@gmail.com

^*Correspondence: Yvan-Claude Raverdy, Independent Researcher, France, Email: ycraverdy@gmail.com

Received: 13-Mar-2023, Manuscript No. puljpam-23-6281; Editor assigned: 14-Mar-2023, Pre QC No. puljpam-23-6281 (PQ); Accepted Date: Mar 30, 2023; Reviewed: 17-Mar-2023 QC No. puljpam-23-6281 (Q); Revised: 18-Mar-2023, Manuscript No. puljpam-23-6281 (R); Published: 31-Mar-2023, DOI: 10.37532/2752-8081.23.7(2).129-133

Citation: Raverdy YC. A formula for electron mass calculation based on new fundamental concepts. J Pure Appl Math. 2023;7(2):129-133.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

We present a novel formula for the mass of the electron as a function of four fundamental constants of electromagnetism and gravitation: the fine structure constant, Planck's constant, the speed of light, and the gravitational constant. We derive the formula in three major steps.
First, we model the electron as a decreasing standing wave, solution of the propagation equation coming from Maxwell's relations. We consider its wave number k0 as a key value of electromagnetism. The internal energy is distributed according to the square of the amplitude of the wave.
Second, we make the hypothesis that the field of the wave has lower and upper bounds. Assuming quantization of kinetic momentum we find that the logarithm of the quotient of these bounds can be assimilated to the inverse of the fine structure constant. Third, we propose that vacuum space is a granular fluid medium. The value k0 is such that it implies opacity of the electron wave to gravitons, which are the elementary dynamic corpuscles of the fluid.

Keywords

Electron mass; Calculation; Fundamental; Novel formula

Introduction

The mass of the electron, which is one of the fundamental constants of physics, is known with high precision by experimental measurement, but the theoretical justification of this mass, as well as of other elementary particles, is still an unsolved problem.

We propose a novel formula for the electron mass in stationary state in a new framework which appeals directly to the ideas which have been at the basis of main theories in force today.

In this context, it is worth recalling the essential contribution of Louis De Broglie, who discovered the wave character of particles and its close relationship with the principles of Special Relativity [1-2]. De Broglie considered a particle as a “small moving clock” along a wave radius and having continually the same phase [3]. We give here, for the first time, a meaning to the expression “small clock”, treating the fundamental nature of the electron as a real physical static wave, solution of Maxwell's equation.

We also recall that the first attempt to explain Newton's force was a Corpuscular theory [1-12].

Our proposal is based on three main axes. First, the fact that the electron can be represented as a decreasing wave, which is a solution of the second order partial differential equation resulting from Maxwell's relations in vacuum.

Second, we bound this wave by two lengths whose quotient logarithm is the fine structure constant. This quotient is obtained by quantization of the angular momentum of the wave function.

Third, the introduction of a corpuscular theory for gravitation furnishes the last element for the establishment of the formula. Respecting the quantization principle we postulate the opacity of the wave with respect to gravitons. This part leads to a novel connection between Electromagnetism and Gravitation.

Presentation of the formula

The formula below gives the value of gravitational inertia which is the mass (m_e) defining the total static internal energy of the electron (m_ec²). It presents the remarkable property of combining the four fundamental constants of electromagnetism and gravitation.

equation

where:

h is Planck's constant,

c is the speed of light in vacuum,

G is the gravitational constant,

ω is a dimensionless quantity comparable to the inverse of thefine structure constant (1/α).

We will return to the value of ω with the numerical evaluation of the formula in 6.

The remainder of this publication is devoted to the justification of the formula.

The internal wave of the electron, solution of the general wave equation

We started from the idea that the second order partial derivative propagation equations resulting from Maxwell's relations are basic for the description of static and massive particles, as well as of dynamic particles without mass.

Indeed, this wave equation:

equation

leads to the Klein-Gordon equation for guided propagation, the nonrelativistic version of which is Schrödinger's equation (11). Another very important tensorial variant is Dirac's equation (4) and (10). These equations proceed from a dynamic point of view and describe all properties of the particle.

We have considered stationary and monochromatic radial (spherical symmetry) solutions of equation (2) which can then be written:

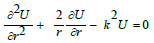
equation

where the first two terms express the Laplacian in polar coordinates depending only on r, and the third term expresses that the phase is monochromatic.

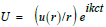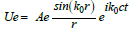
The main solution in the form equation , setting k = k₀ (cf. section 5) is:

equation

This solution presents the essential advantage of being convergent for r → 0 . It seems natural to attribute this solution to the electron because of its variation with 1/r, reminiscent of the electrostatic potential.

We also make the assumption that the wave field is bounded by lower and upper values, respectively l₀ and R, these values will be interpreted [9].

Using these elements, we write a first formula for the internal energy with values proportional to the square of the amplitude of the wave, depending on r only.

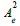equation

equation is the coefficient of elementary electrostatic field energy, so

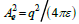
equation

where q is the elementary charge and ε the dielectric constant in vacuum (with an approximation discussed).

Given that the extremal values l₀ and R are, as we will see, respectively very small and very large, the value of the integral (3) can be calculated by integration from 0 to ∞ .

equation

Internal angular momentum

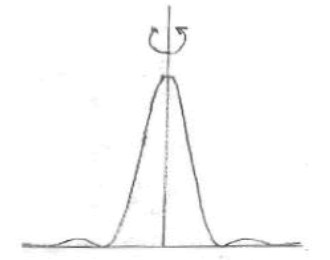
As we said, it is considered that the internal energy of the electron is distributed in space according to the value of the square of decreasing spherical wave amplitude expressed by the function sin²(kr)/r²

A quick calculation shows that approximately 85% of this energy belongs to the central pulsation. To go further it is necessary to dimension the structure, and we have to consider the existence of the internal angular momentum. The particle is modeled as a complex vortex inside the uid medium constituting the vacuum [6-7]. One component of the angular momentum then is the rotational vector, product of the impulse momentum vector and the radius vector, and whose modulus m (m=m_ecr) can be related to the internal orbital angular momentum (Figure 1).

Figure 1: Using formula (3) we express the absolute value of this component by the integral

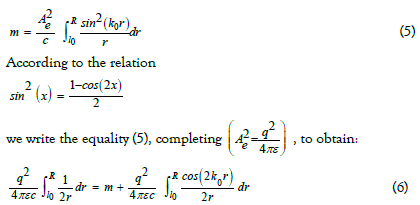
equation

We compare this equality to the quantum composition of the Internal kinetic momentum, which is the sum of an Electro-magnetic (m) and an Only-magnetic (s), similarly to some solutions of Dirac equation, whose values are intrinsic to the particle. We assume that the terms of this equality are the projections of the modules of the vectors expressing the orbital and magnetic moments. So the first member can be assimilated to the quantum value of the total momentum (internal angular momentum) whose value is 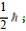equation then solving the integral allows us to write:

equation

This equality implies the equivalence of ln 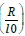equation with inverse of the fine structure constant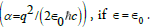

As an appendix we present the result of an electromagnetic energy model, which confirms this equivalence, it is also a way to emphasize the importance of this result.

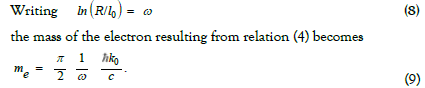
equation

We will not discuss here the calculation of the integrals relative to m and s, which would lead beyond the scope of our presentation which is the simple justification of the formula for the mass of the electron. This result justifies the application of the limits R and l₀ , calculated in the next chapter, to the wave of the electron, in virtue of the equivalence of ln (R/l₀) to the inverse of the fine structure constant, in the approximation discussed in chapter 6.

The wave number k₀

We formulate the hypothesis that the value of k₀ corresponds to a common vibration frequency for all elementary particles with spin 1/2, it must be considered as a universal constant. For a massive boson, the wave number is k = 2k₀ .

To determine its value, we consider that the empty space is constituted by a quantum character uid which underlies our corpuscular interpretation of gravitation [5].

In this medium, each elementary particle is reacting with the uid medium, the interaction results in the exchange of an elementary action h for each vibration period of the wave particle.

This exchange corresponds to the emission of a graviton which is a wave of minimal impulse (μ₀c) corresponding to the propagation of an elementary constituent deficit inside the quantum fluid medium. In this context, 2k₀ is defined as the wave number of a photon with minimal electromagnetic energy, the wave section of which is opaque to gravitons.

Gravitons are the particles producing the gravitational force by exchange of an elementary action h with particles of matter.

This principle of minimality then applies to all elementary particles which thus see their vibration frequency fixed at k₀c for fermions, and 2k₀c for massive bosons.

The electromagnetic wave section corresponds to half the surface of a wavelength which figures the vortex and where the total energy of the wave is distributed.

Why such a definition? The idea is to establish a criterion for applying Newton's laws to elementary particles based on particle wave opacity (at minimum) to gravitons, which confers a quantum character to gravitation, because for this case a single graviton must react with the entire electron within its cross section.

For the calculation of k₀ consider first the value l₀ introduced in chapter3.

We suggest that l₀ , which is the lower bound of the electron wave field, is also the shortest elementary interval, that is to say the length of the building block for all physical beings, including the associated graviton.

In our corpuscular theory of Gravitation, a mass M is both emitting and absorbing gravitons, Newton's force is due to the capture of graviton impulse by the receiving mass.

The calculation of l₀ is carried out by identification of this strength with the gravity pressure P_g resulting from a mass M exerted on a mass M ' .

We consider that the mass M emits N gravitons per second through an area of 4πr² , N is the quantum frequency Mc² / h , which amounts to consider the additivity of the frequencies for each particle constituting the mass M .

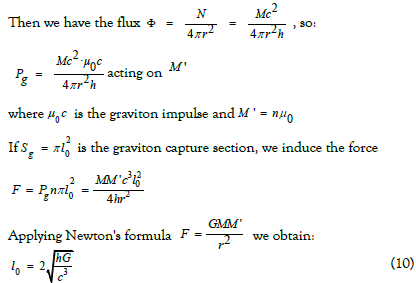
equation

This length is close to the Planck length 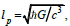equation it is a cornerstone of our corpuscular theory which interprets this quantity as the dimension of the graviton.

It remains to write that the k vortex-wave surface is opaque to gravitons whose cross section is 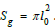equation

The k wave energy is uniformly distributed over the surface S_k which corresponds to the wave vortex section with diameter λ / 2 .So we have S_k = πλ²/16 in correspondence of the section 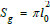equation of gravitons. We can then write the vortex-wave opacity criterion

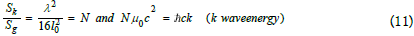
equation

Let us now consider the quantity R, the maximum range of the field of the wave. We formulate the hypothesis that this length is also the radius of the material universe [9], it is, moreover, the range of the electromagnetic field and also the distance corresponding to the elementary action h of a graviton, whose momentum is u₀c, we then have:

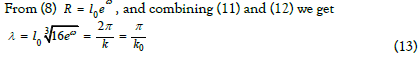
equation

It suffices to copy this value of k₀ into relation (9) expressing the value of l₀ given by relation (10) to obtain the formula giving the mass of the electron.

One can easily compute the numerical values of the constants determined by the formulas (10), (8), (13), (12) (setting. ω = 137.0036 see next paragraph):

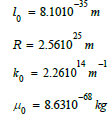
equation

Numerical evaluation of the formula

Using formula (1) one can easily calculate the numerical value of the mass of the electron. The calculation with the following values (CODATA 2018 values):

equation

produces the result m_e=9.009374 10^-31 kg, to be compared with the known value 9.1093837015(28) 10^-31 kg of the mass of the electron. The relative discrepancy is about 1%.

From this comparison, we draw a double conclusion: on the one hand, given the quality of the result, the formula appears valid, but, on the other hand, there is a difference that requires an explanation. We first note that the calculation is extremely sensitive to the value of : it suffices to choose a value of ω = 137.0036 i.e .decreasing by a factor of 2/10000 to obtain the result me=9.1094 10^-31 kg.

We propose the following explanation: Vacuum is a dielectric medium, and α is depending on the dielectric constant 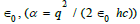equation but this vacuum is not an entirely homogeneous medium since it contains at least the electromagnetic radiations in addition to the basic fluid medium. The energy density of these radiations remains much lower than that of the total vacuum energy evaluated by General Relativity.

The analysis of Planck satellite images makes it possible to estimate the proportion of radiations with respect to the total energy of the vacuum.

This proportion is approximately 1=10000, which is about half of the relative difference between 1 / α and ω.

Thus our formula, which uses the quantity could serve as a basis for determining the radiation part of vacuum energy. Inversely, the knowledge of total radiation energy would give more precision to the numerical evaluation of the formula.

Conclusion

The formula we arrived at clearly is valid, and we think that it can serve as a springboard for the calculation of other parameters of the standard model. Should we transform our vision of corpuscles, fields and gravity? The concrete image and simple interpretation of the electron we described are maybe part of the answer.

It seems to us that deepening the elements at the base of this article, one can also establish criteria about the nature and the very existence of elementary particles and mass energy identification with that of its wave.

It would be interesting to apply this method to link the mass of the diversity of particles to the various solutions of wave equations (as in (2)), with a quantized angular momentum of multiples of h / 2 . Our result obtained for the electron must nevertheless be integrated with the dynamics of the particle, subject of multiple studies.

To go further, we believe that a gravitational theory compatible with quantum physics must give a conceptual interpretation to the spacetime of Relativity.

The idea of a granular fluid, associated with a corpuscular point of view for gravitation should be a promising approach.

In our view, this paper expresses an important result based on simple physical concepts developed from de Broglie's ideas: it renders precise the profound wave nature of the electron, as well as of other fundamental particles, and proposes a concrete description of vacuum space supporting the space-time used in Relativity.

Appendix: The elementary electromagnetic wave as a resonant circuit

The elementary electromagnetic wave is assimilated to a resonant circuit, this is a model borrowed from macroscopic physics, which does not claim to give a description of the electromagnetic wave, and still less the wave of the electron; its interest is to clarify the hypothesis of the limitation of the electric field limitation with lower and upper values.

We have assumed that these limits are applicable to the wave of the electron.

If L and C are respectively the inductance and the capacitance of a cylindrical geometry circuit of length l, the resonance frequency is 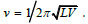equation

We take this frequency for the frequency of a electromagnetic wave to obtain v = c / λ with λ = 2πl

The energy of this wave can be identified with the energy of the circuit:

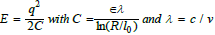
equation

where q is the elementary charge, ε , l₀ and R, respectively, the minimum and maximum radii of the capacitor, which we consider as lower and upper range of the electrostatic field.

Setting the oscillation frequency of the circuit equal to the quantum frequency we obtain

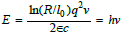
equation

This double equality allows us to introduce by writing:

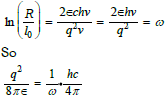
equation

Which shows 1 / ω to be the fine structure constant if ε = ε⁰ and thus corroborates the result obtained by the quantization of the angular momentum in chapter 4.