A numerical method for solving 3D inverse scattering problem with non-over-determined data

Received: 14-Jul-2017 Accepted Date: Aug 11, 2017; Published: 15-Aug-2017, DOI: 10.37532/2752-8081.17.1.1

Citation: Ramm AG. A numerical method for solving 3d inverse scattering problem with non-over-determined data. J Pur Appl Math. 2017;1(1):1-2.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

A new numerical method is given for solving 3D inverse scattering problem (ISP) with non-over-determined scattering data. No such results were known. The ISP is not solved by a parameter fitting procedure. The method is based on the author’s uniqueness theorem. The data are the values of the scattering amplitude for all β∈S²β, where S²β is an open subset of the unit sphere S² in ℝ³, α₀ ∈ S² is fixed, and all k ∈ (a,b), where 0 ≤ a < b. The basic uniqueness theorem for solving the inverse scattering problem with non-over-determined scattering data belongs to the author. Earlier there were no results on numerical methods for solving the inverse scattering problem with such data. The proposed numerical method for solving the inverse scattering problem is original. It is based on the author’s uniqueness theorem and on his method for stable solution of ill-conditioned linear algebraic systems. Since the inverse scattering problem is non-linear, it is of prime interest that the basic step of the proposed inversion procedure consists of solving linear algebraic system.

Keywords

Inverse scattering; Numerical solution; Non-over-determined scattering data

The inverse scattering problem consists of finding the unknown potential q(x) from the scattering data. These data are the values of the scattering amplitude A(β, α, k) at some values of β, α, k. The inverse scattering problem is a major theoretical problem of physics which has huge practical significance.

The basic uniqueness theorem for solving the inverse scattering problem with non-over- determined scattering data belongs to the author [1]. This result was not known for decades. There were no results on numerical methods for solving the inverse scattering problem with non-over-determined data.

The inverse scattering problem is highly non-linear because the scattering amplitude depends non-linearly on the potential. Therefore, it is remarkable that the inversion procedure proposed in this paper is linear: it is reduced to numerical solution of a linear algebraic system, see system below. No such results were known. The ISP is not solved by a parameter fitting procedure. The numerical method is based on the author’s uniqueness theorem [1].

The scattering solution is the unique solution to the following problem:

(∇² + k² − q(x) u = 0 in ℝ³,           (1)

u = e^ikα.x + v ,          (2)

where v is the scattered field satisfying the radiation condition,

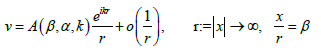         (3)

where α, β ∈ S², S² is the unit sphere, β is the direction of the scattered wave, α is the direction of the incident wave, k2 > 0 is energy, k > 0 is a constant. The function A(β, α, k), the scattering amplitude, can be measured experimentally. Let us call it the scattering data.

We assume throughout that q is a real-valued compactly supported function with support D, q = 0 for x ∈ D⊂{ x : max_j | x_j | ≤ R} , and q is C¹-smooth. The set of such q let us call Q.

It is known that the solution to the scattering problem (equations 1-3) does exist and is unique. The inverse scattering problem (IP) consists of finding ∈ Q from the scattering data.

It was first proved by A.G. Ramm’s [2,3] that q ∈ Q is uniquely determined by the scattering data A(β, α, k₀) known for a fixed k = k₀ > 0 and all β ∈ S_β² and all α ∈ Sα 2, where S_β² is an open subset of S².

Ramm gave a method for solving inverse scattering problem with fixed-energy data and obtained an error estimate for the solution for exact data and also for noisy data [3,4].

The goal of this paper is to give a numerical method for solving the inverse scattering problem with non-over-determined scattering data. The non-overdetermined scattering data are the data that depend on the same number of variables as the potential, that is, on three variables. In this paper we assume that these data are the values of A(β, k) := A(β, α₀, k) known for all β ∈ S_β², for all k ∈ (a, b), 0 ≤ a < b, and a fixed α₀ ∈ S².

Our method for solving this inverse scattering problem is described in Section 2. This problem is reduced to solving linear algebraic system which is very ill-conditioned.

Therefore, numerically one should use DSM (Dynamical Systems Method), a stable method for solving linear algebraic system (equation 8) (or other stable methods for numerical solution of ill-conditioned linear algebraic systems) [5,6]. Stable solution of equation 8 is the main numerical difficulty of our method. This method is not a parameter fitting method, which is a big advantage of the method. There were no numerical methods for solving the inverse scattering problem with non-over-determined data. The theoretical basis for our paper is the uniqueness theorem proved by the author [1].

Inversion method

The scattering problem is equivalent to the standard integral equation [3]:

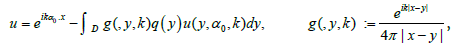          (4)

where the integral is taken over the support of q(x) and the dependence on the fixed vector α₀ is dropped in what follows. Define

h := q(x)u(x,k)           (5)

Equation (4) implies the following equation for h:

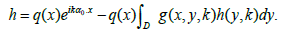          (6)

From (4) one derives the following exact formula for the scattering amplitude:

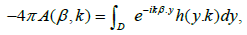           (7)

where β ∈ S² and k ∈ (a, b). Recall that we write A(β, k) for A(β, α₀, k) and h(x, k) for h(x, α₀, k).

If A(β, k) is known, then equation (7) is a linear integral equation of the first kind with respect to the unknown h(y, k). If h is found, then q can be found by formula (9) below.

Let us partition the support of q into a union of P small cubes Δ_p. Choose a point y_p ∈ Δ_p, 1 ≤ p ≤ P, in each of the small cubes. Denote by Δ the volume of each small cube. Choose P different points k_m ∈ (a, b), 1 ≤ m ≤ P. Denote h_pm := h(y_p, k_m). Choose P different vectors β_j ∈ S² β , 1 ≤ j ≤ P. Discretize equation (7):

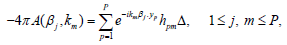          (8)

where Δ is the element of the volume of the support of q.

Equation (8) is a linear algebraic system of P2 equations for P2 unknowns h_pm, 1 ≤ p, m, j ≤ P. If this system is solved numerically, then equation (6) yields the values q(x_p) of the unknown potential:

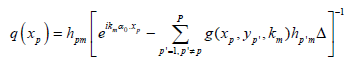,           (9)

where 1 ≤ p ≤ P, and the right side of equation (9) should not depend on m or j.

Although the right side of equation (9) does not depend on j explicitly, it does depend on j implicitly since there is a dependence on j in equation (8), so that the solution h_pm of equation (8) does depend on j.

The independence of q(x) and, therefore, the right side of equation (9) on m and j is an important requirement in the numerical solution of the inverse scattering problem, a compatibility condition for the data. This requirement is automatically satisfied for the limiting integral equation formula:

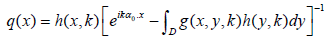          (10)

which follows from equation (6)?

The values q(y_p) essentially determine the C¹-smooth potential q if the distance between the neighboring points y_p is sufficiently small.

The linear algebraic system (8) is very ill-conditioned because it comes from an integral equation of the first kind with an analytic kernel. From the author’s uniqueness theorem it follows that the non-over-determined scattering data A(β, k) determine uniquely the potential q ∈ Q, see [2].

Thus, one expects that the proposed method can be numerically efficient if the linear algebraic system (8) is solved stably. Theoretical methods for stable solution of linear algebraic systems are developed which finds many numerical examples of such solutions [5,6].

There were no numerical methods for solving the inverse scattering problem with non- over-determined data, as far as the author knows.

One can choose β_j and k_m so that the determinant of the linear algebraic system (8) is not equal to zero, so that the system is uniquely solvable. This does not eliminate the essential difficulties in numerical solution of the inverse scattering problem caused by the numerical difficulties in solving severely ill-condioned linear algebraic systems.

In conclusion let us prove the following lemma.

Lemma 1 There exist β_j ∈ S² β and k_m ∈ (a, b), 1 ≤ j, m ≤ P, such that

.

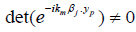In this lemma the matrix depends on m, p. The index j enters as a parameter, 1 ≤ m, p ≤ P, 1 ≤ j ≤ P.

Proof of Lemma 1. Let β_j ∈ S² β be arbitrary fixed, p ≠ p ' if p ≠ p ' and 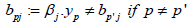. Let us prove that there are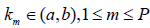, such that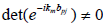. Assume the contrary. Then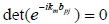. for any choice of k_m The function 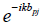is analytic (entire) with respect to k . Therefore, if the above determinant vanishes for all k₁ = k , then it vanishes identically with respect to k , so that the set of function is linearly dependent. This is a contradiction since the above set is linearly independent under our assumption, namely the assumption that 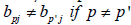. Indeed, if c_p are constants and 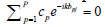for all k ∈ (a,b), then, by analyticity, 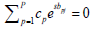for all s ∈ R. Since all numbers pj b are different and real-valued, they can be ordered. Let us assume without loss of generality that b₁ > b₂ >..... b_p , where 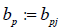Then, the relation 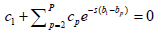for s → +∞ yields c₁ = 0 . Similarly one proves that c_p=0 for all p. This contradicts to the linear dependence of the system. Lemma 1 is proved.

REFERENCES

1. Ramm A. Uniqueness of the solution to inverse scattering problem with scattering data at a fixed direction of the incident wave. Journal of Mathematical Physics. 2011;52:123506.
2. Ramm A. Recovery of the potential from fixed-energy scattering data. Inverse problems. 1988;4:877.
3. Ramm A. Inverse problems, Springer, New York, 2005.
4. Ramm A. Stability of the solutions to inverse scattering problems with fixed-energy data. Milan Journal of Mathematics. 2002;70:97-161.
5. Ramm A. Dynamical systems method for solving operator equations, Elsevier, Amsterdam, 2007.
6. Ramm A, Hoang NS. Dynamical Systems Method and Applications: Theoretical Developments and Numerical Examples. Wiley, Hoboken, 2012.