A probabilistic proof of the multinomial theorem following the number $A_n^p$

Received: 03-May-2023, Manuscript No. puljpam--23-6397; Editor assigned: 08-May-2023, Pre QC No. puljpam--23-6397(PQ); Accepted Date: May 29, 2023; Reviewed: 11-May-2023 QC No. puljpam--23-6397(Q); Revised: 15-May-2023, Manuscript No. puljpam--23-6397(R); Published: 31-May-2023, DOI: 10.37532/2752-8081.23.7(3).202-203

Citation: Dekpe A. A probabilistic proof of the multinomial theorem following the number A^p_n. J Pure Appl Math. 2023; 7(3):202-203.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

In this note, we give an alternate proof of the multinomial theorem following the number A^p_n using probabilistic approach. Although the multinomial theorem following the number A^p_n is a combinatorial result, our proof may be simple for a student familiar with only basic probability concepts.

Key Words

Probabilistic Proof; Multinomial Theorem; Probability; Number

Introduction

The following multinomial theorem based on number n^p (development based on a power of a number) is an important result with many applications in mathematics statistics and computations. The theorem states as follows:

Theorem 1

Let n and m be non-zero natural numbers, x₁, x₂, ..., x_m real numbers:

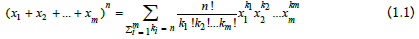
where k_i are natural integers.

For readers interested, they can see reference for further interpretation [1]. Recently, we have published another type of multinomial theorem based on numbers $A_n^P$ and given some applications in the case of binomials [2]. (see [1] for more details). In each case, the first demonstrations are based on a proof by induction using the binomial formula. A. Rosalsky proposed a probabilistic approach to this proof in the case of binomials which will be generalized to the multinomial theorem by Kuldeep Kumar Kataria [3-4]. An urn contains x₁ balls numbered 1, x₂ balls numbered 2, x_m balls numbered m, such that the total number of balls is 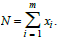Consider an experiment where we draw a ball from the urn without replacement, and note the number on it each time. By repeating this experiment n times [5-6]. The probability mass function of the variables x₁, x₂, ..., x_m is:

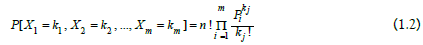
Where, 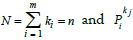the probability of having the balls numbered i k_j times.

From (1.2) we have:

Next, we will establish and prove the multinomial theorem following the number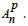

A PROBABILISTIC PROOF OF THE MULTINOMIAL THEOREM FOLLOWING THE NUMBER $A_n^P$

Theorem 2

Let m and n be two non-zero natural numbers and x₁, x₂, ..., x_m natural numbers. Then,

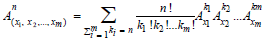
Where k_i are non-negative integers, k_i ≤ x_i and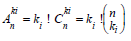

Proof: Let us consider:

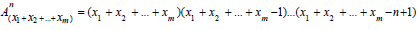
Using the distributives property without resuming the number on the right side of the equation, it follows that for any natural numbers we have :

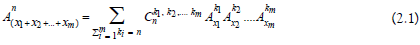
Where 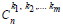are positive integers and are non-negative integer’s satisfying 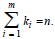We just need to show that.

We have n ≥ x_i for i = 1, 2, ....,m Let’s put:

Where 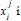is the remaining number of the balls numbered i before the j^th draw. 0 ≤ p_i ( j ) ≤ 1 substituting (2.3) in (1.3) we obtain

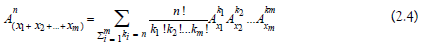
finally the subtraction of (2.4) from (2.1) gives:

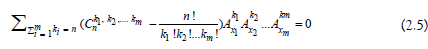
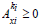since (2.5) is a zero polynomial in m variables, (2.2) follows and the proof is complete.

References

1. A Dekpe. Mutinomial development. 2023;1-18

   [Google Scholar] [Crossref]

2. D Dacunha-Castelle, M Duflo. Exercise de probalites et statistiques. Masson, Paris. 1982;1

   [Google Scholar] [Crossref]

3. A Rosalsky. A simple and probabilistic proof of the binomial theorem. Amer statist. 2007;61(2):161-62

   [Google Scholar] [Crossref]

4. K K Kataria. A Probabilistic proof of the multinomial.  Amer Math Monthly. 2016;123(1):94-96

   [Google Scholar] [Crossref]

5. K K Kataria. Some Probabilistic interpretation of the multinomial theorem. Math Mag. 2017;90(3):224-24
6. S Abbas. Multinomial theorem Procured from Partial differential equation. Appl Math E-notes. 2022;22:457-59

   [Google Scholar] [Crossref]