A sequential and parallel algorithm for disjoint cliques problem on interval graphs
Received: 19-Nov-2018 Accepted Date: Nov 28, 2018; Published: 07-Dec-2018, DOI: 10.37532/2752-8081.18.2.10
Citation: Mondal S. A sequential and parallel algorithm for disjoint cliques problem on interval graphs. J Pur Appl Math. 2018;2(3):05-7.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
Using DAG approach,A sequential algorithm is presented to solve disjoint cliques problem on interval graph G which takes O(n^2) time where n is the number of vertices of the graph. For the same problem a O(log2n) time parallel algorithm is presented which takes  processors on an EREW PRAM model. Also, on a CREW model it takes O(logn) time with O(n^(3+ε) ),ε>0 processors.
processors on an EREW PRAM model. Also, on a CREW model it takes O(logn) time with O(n^(3+ε) ),ε>0 processors.
Keywords
Design of algorithms; Analysis of algorithms; Cliques; Disjoint cliques; Interval graphs.
AMS Mathematics Subject Classification (2010): 05C62, 05C78, 05C85, 68Q22, 68Q25, 68R10
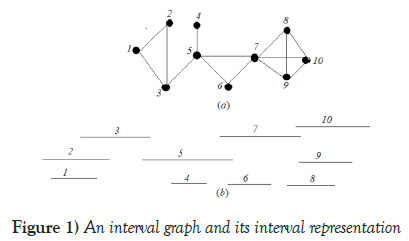
An undirected graph G=(V,E) is an interval graph if the vertex set V can be put into one-to-one correspondence with a set I of intervals on the real line such that two vertices are adjacent in G iff their corresponding intervals in I have non-empty intersection. The set I is called an interval representation of the graph G and G is referred to as the intersection graph of I [1].
Interval graphs arise in the process of modeling real life situations, specially involving time dependencies or other restrictions that are linear in nature [2-7]. This graph models are convenient for analysis of electric circuits, VLSI design and layout routing process, scheduling, design of complex data structures, archeology, molecular biology, psychology, scheduling transportation etc. Recently Interval graphs have found applications in protein sequencing [8], macro substitution [9], circuit routing [10], file organization and job scheduling [11], resister allocation, routing of two points nets [12] and many others.
For a simple connected graph G=(V,E), a subset of V is said to be a clique in G if every pair of vertices of this subset is connected by an edge of E. A maximal clique is a clique to which no further vertex of the graph can be can be added so that it remains clique. A maximum clique is maximal clique cardinality. The cardinality of the maximum clique is called the clique number. If k be the total number of maximal cliques of the graph G and C={C_1,C_2,… C_k} be the set of all maximal cliques of the graph, then a subset D of C (D ⊆ C) is said to be a ‘set of pairwise disjoint cliques if every pair of cliques in D is disjoint.
Survey
For an arbitrary undirected graphs, disjoint union of cliques is easily seen to be NP-complete. As the disjoint union of the cliques problem is a ‘hard’ problem, so, we can explore its restrictions to special class of graphs and we hope to detect computationally better tractable cases. The motivation for this approach comes from the NP-completeness table of Johnson [13], where the complexity of ten different graph problems restricted to a series of graph classes is given. Two problems in the table of Johnson are the above mentioned ‘clique’ and ‘partition into cliques’ problem.
The problem ‘disjoint union of cliques’ was analyzed first by Frank [14]. He considered comparability graphs and its complement graphs (cocomparability graphs) and given an algorithm for both graph classes with complexity O(a b n2),where a is the cardinality of a maximum clique and b is the cardinality of a maximum independent set. Gavril et al. [15] proposed a slightly better algorithm which needs O (Dn2) time steps for comparibility graphs and O (n3+ b n2 log n) for co-comparability graphs. In [16], for subclass like the interval graphs, bipartite graphs and co graphs with n vertices, Jansen et al. have designed an algorithm for finding D paiwise disjoint union cliques in O(Dn2), O(m√n) and O(n2) time respectively.
In this paper, a sequential algorithm and a parallel algorithm are presented to find a set of pairwise disjoint cliques in the interval graph with maximum overall number of vertices. The time complexity of the proposed sequential algorithm is O(n2) whereas the parallel algorithm takes O(log2n) time with  processors on an EREW PRAM model and on a CREW model it takes O(log n) time with O(n3+ε),ε>0 processors, where n is the number of vertices of the graph.
processors on an EREW PRAM model and on a CREW model it takes O(log n) time with O(n3+ε),ε>0 processors, where n is the number of vertices of the graph.
Data Structure and Preliminaries
Let I= {I1, I2,… In}, be the interval representation of the interval graph G= (V,E), where ar is the left endpoint and br is the right endpoint of the interval Ir=[ar,br] for all r=1,2,… n. Without loss of generality, we assume the following:
1. the intervals in I are indexed by increasing right endpoint, i.e., b_1<b_2<⋯<b_n,
2. the intervals are closed, i.e., contains both of its endpoints and that no two intervals share a common endpoint,
3. vertices of the interval graph and the intervals on the real line are one and the same thing,
4. the interval graph G is connected, and the list of sorted end points is given.
Considering the location of 2n endpoints of the n intervals on the real line in increasing order and the array e= {e(1),e(2),. . . , e(2n)} is formed. For each element e (i) of e, two fields e (i).ver and e (i).type are defined as follows:
e(i).ver=k, if e(i) is the end point of the interval Ik.
e(i).type={a, if the end point e (i) is left end point
={b, if the end point e (i) is right end point.
Then, we define a new field e (i).max to the array e as
e (i).max=e(i).ver for i=1.
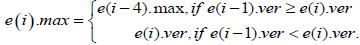 Thus, the fields e(i).max
Thus, the fields e(i).max
computes the maximum vertex between the end points e(1) and e(i).
For the graph of Figure 1, the array e is shown in the Table 1.
| e | e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 | e9 | e10 | e11 | e12 | e13 | e14 | e15 | e16 | e17 | e18 | e19 | e20 |
| e(i).ver | 2 | 1 | 3 | 1 | 2 | 5 | 3 | 4 | 4 | 7 | 6 | 5 | 6 | 8 | 9 | 10 | 7 | 8 | 9 | 10 |
| e(i).type | a | a | a | b | b | a | b | a | b | a | a | b | b | a | a | a | b | b | b | b |
| e(i).max | 2 | 2 | 3 | 3 | 3 | 5 | 5 | 5 | 5 | 7 | 7 | 7 | 7 | 8 | 9 | 10 | 10 | 10 | 10 | 10 |
Table 1. To find the disjoint cliques on interval graphs, we have to first compute all maximal cliques and the time complexity of which given in the following lemma.
Lemma-1
All maximal cliques of an interval graph can be computed sequentially in O(n+γ) time, where γ is the output size and in parallel in 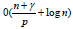 time using p processors on an EREW PRAM [17].
time using p processors on an EREW PRAM [17].
One more important characterization of the interval graph with respect to cliques is given by Gilmore and Hoffman [18]. It is stated as follows:
Lemma-2
A graph G is an interval graph if and only if the maximal cliques of G can be linearly ordered in such a way that for every vertex v of G, the maximal cliques containing v occur consecutively [18].
Using Lemma-1, we can determine all maximal cliques. Let the total number of maximal cliques thus found be α. As the graph G is an interval graph, these α maximal cliques can be ordered by Lemma-2. Let the set of these ordered maximal cliques be {C1, C2,…Cα}. We also consider two fictitious cliques C0 and C (α+1) and take them as null set. Thus the ordered maximal cliques becomes {Cα,C1,C2,… Cα, Cα+1}.
Another array, denoted by max (Ci), is defined as
max (Ci ) =max{v: v∈C_i}.
This array gives the maximum vertex that the clique Ci contains.
From Lemma-2, it follows that if u∈Ci and u∈Ck where I ≤ k, then u∈C_j for all I ≤ j ≤ k. If p(u) is the largest subscript of the maximal cliques in which u belongs, then we call the clique Cp(u) as end clique of u, i.e., if p(u)=max∈{j: u∈Cj} then the end clique of u is Cp(u). We note that p(u) forms an array for all u∈V, and also we note that if j>p(u) then u ∉Cj.
Next, we define another important array First Disjoint (Ci), i=1,2,…,α is defined as follows:
FirstDisjoint (Ci) =p(max(Ci ) )+1.
From this definition and the ordering of maximal cliques done by Lemma-2, it follows that if j=FirstDisjoint (Ci) then all the cliques Cj,C(j+1),…,Cα are disjoint with Ci and Cj is the first disjoint clique of the clique Ci.
For any two consecutive cliques we have the following lemma.
Lemma-3
Any two consecutive cliques Ci and Ci+1 are non-disjoint cliques in G.
Proof: If possible let Cj and Cj+1 are disjoint cliques in G. Then from the ordering of maximal cliques, it is clear that Cj is disjoint with all cliques Cj+1, Cj+2, … , Cα. From Lemma-2, we have
for any i ≤ j, if u ∈ Ci then the end clique of u cannot be ck where k ≥ j + 1, since in that case u must belongs to both Cj and Cj+1 contradicting the fact that Cj and Cj+1 are disjoint. As it
is true for any u ∈ Ci, we have Ci is disjoint with ck for any k ≥ j + 1. Hence, any one among
C1, C2, … Cj is disjoint with any Cj+1, <Cj+2, … , Cα. This means the graph G is disconnected
which is not true. Hence, any two consecutive cliques Ci and Ci+1 are nondisjoint cliques in G.
This proves the lemma.
The array FirstDisjoint plays an important role for construction of the network N. An algorithm to compute this array is presented below:
Algorithm FD
Input: The array (i), i = 1, 2, … , 2n for interval graph.
Output: The array FirstDisjoint.
Step-1: Compute all maximal cliques , i = 1, 2,. . . , α.
Step-2: Compute all max ( ) , i = 1, 2, . . . , α.
Step-3: Compute all (i), i = 1, 2, . . . , n.
Step-4: For all i = 1, 2, . . . , α calculate
FirstDisjoint ( ) = ((C )) + 1. end FD
The complexity of Algorithm FD is given below:
Theorem-1: Algorithm FD can be computed in (n2) time in sequential.
Proof. Step-1 can be computed in (n + γ) time, where γ is the sum of cardinalities of all cliques which is known and to be (n + m) time, where m is the number of edges of the graph [7]. In step-2, for each i = 1, 2,. .. , α, the array max ( ) takes (|Ci |) time, i.e., (n) time. Hence, for all cliques it takes (α n) time, i.e., (n2) time as α is of (n). Similarly, Step-3 and Step-4 takes (n2) time. Therefore, overall time complexity of the Algorithm FD is of (n2). Hence the theorem.
Using the array FirstDisjoint anyone can construct the network N, called as Directed Acyclic
Graph (DAG).
A Network and its Properties
A Network
A network N consists of a finite set of nodes VN = {A0, A1, … Am} together with a set of arcs
EN of all ordered disjoint pairs (Ai, ), j > i; i, j = 0, 1, … , m. The network N has also a
special return arc (Am, A0) from the sink Am to the source A0. With each arc (Ai,) ∈ EN of the network N, a non-negative weight w(Ai,Aj ) is associated. A path having maximum total weight among all paths from A0 to Am is called the maximum weight path.
Let T be the set of all paths from the source A0 to the sink Am in N. Then T is a finite set. For any path P ∈ T let the sum of the weights for the arcs associated with the path P is (P).
The maximum weighted path problem for a network N is the problem of finding maximum weighted path, i.e., it is a problem of finding a path P∗ from A0 to Am in the network N for which the total weight is maximum. So, it is a problem of finding a path P∗∈ T such that
w(P∗) = max{w(P) ∶ P ∈ T}.
Construction of the Network
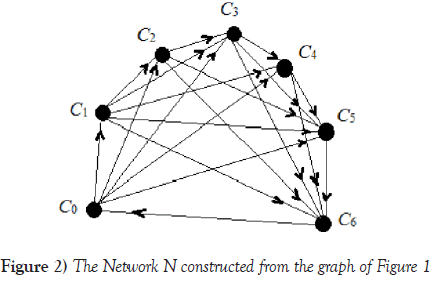
We now supposed to construct a network N so that a maximum weighted path of it leads to the solution of pairwise disjoint cliques problem in the interval graph G Figure 2.
The nodes of the network are taken as the set of all maximal cliques VN = {C0, C1, … Cα , Cα+1} and the set EN of arcs is formed by e −arcs, d −arcs and special return arc defined respectively as
i) all ordered disjoint pairs (Ci , Cj ), j > i, i, j = 0, 1, 2, … α + 1;
ii) all ordered non-disjoint pairs (Ci−1, Ci ), i = 1, 2, … , α; and
iii) the ordered pair (Cα+1, C0).
As from Lemma-3, the consecutive cliques are always non-disjoint, the weight of all d −arcs are taken zero. The weight of all e −arcs are taken as follows:
i) if the graph G is non-weighted then
w(Ci , Cj ) = w(Ci ) = |Ci |,
i.e., weight of the arc (Ci, ) is equal to the cardinality of the clique Ci; and
ii) if the graph G is weighted then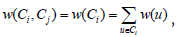
i.e., weight of the arc (Ci, ) is equal to the weight of the node Ci which is the sum of the weights associated with each vertex of the maximal clique Ci.
In N, let the total number of paths from the source C0 to the sink Cα+1 be ℎ, and the set of all such paths be T = {P1, P2, …, Pℎ}. Then for any path Pλ ∈ T we have 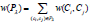 The maximum weighted path problem is the problem of finding the path P∗ ∈ T such that (P∗) = {(P) ∶ P ∈ T} = {(P1), (P2), . , w(Pℎ)}.
The maximum weighted path problem is the problem of finding the path P∗ ∈ T such that (P∗) = {(P) ∶ P ∈ T} = {(P1), (P2), . , w(Pℎ)}.
Next, we shall discuss about the total number of nodes and total computational time.
Lemma-4 The total number of nodes in N is α + 2 and the total number of arcs in N is of (α2) where α < n.
Proof: From definition and construction of N it is clear that the total number of nodes α + 2. The Number of e −arcs starting from each node Ci is at most α. As there are α + 2 nodes in N therefore, the total number of arcs in N is of (α2).
Lemma-5
If all the maximal cliques are given then the time taken to construct the network N is of (α2).
Proof : It follows directly from the Lemma-4.
If D be the set of maximal mutually disjoint cliques of the graph G, then the weight (D) of D is defined as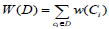 .
.
Thus, ‘Disjoint Clique Problem’ reduces to find a set D of mutually disjoint cliques such that (D) is maximum among all possible (D)’s. Let D∗ be the set of disjoint cliques giving maximum value of (D) then (D∗) = {(D): D is set of mutually disjoint cliques of G}.
Lemma-6
If ( , Cj ) and (Cj, ck ) are any two e −arcs of the network N then (Ci , ck ) is an e −arc.
Proof: Let ( , Cj ) and (Cj, ck ) be any two e −arcs of the network N. Therefore, it follows that Ci, Cj are disjoint cliques as well as Cj, k are disjoint cliques. From Lemma-3 we have j ≥ FirstDisjoint (Ci)>i+1andk≥ FirstD(Cj) > j + 1. That implies k >
FirstD(Ci ) and hence Ci is disjoint with Ck. That is, (Ci, ) is an e −arc.
Let the set of arcs associated with the path P be Q. Now, if P∗ is the path from C0 to Cα+1 whose weight is maximum among all other paths from C0 to Cα+1, then
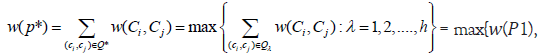
w(P2), … , w(Pλ)},
where Q∗ is the set of arcs associated with the paths P∗. Let Q1∗ and Q2∗ be the set of e −arcs and d −arcs of Q∗, respectively. Hence,
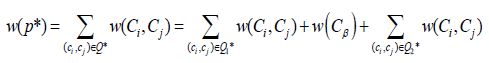
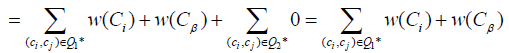
where Cβ is the last node associated with the last arc ( , Cβ ) ∈Q∗.
Let the set of nodes associated with the e −arcs of the path P∗ be PV∗, i.e., PV∗ is the set of nodes Ck’s which form the set of ordered pair arcs Q1∗. Again, as the weight of the arc (Ci, Cj) is the weight of the node Ci, therefore, we may write
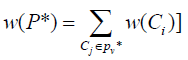
Now, from Lemma-6 we have the following lemma.
Lemma-7. All the cliques of the interval graph G on any path from any node Ci to any other node and Cj , 1 ≤ i, j ≤ α + 1 are disjoint.
The time complexity to find maximum weighted path from C0 to Cα+1 is proved in the following lemma.
Lemma-8.The maximum weighted path from C0 to Cα+1 can be computed in (α2) time.
Proof.Using the algorithms of Ahuja et al. [19] we can compute the maximum weighted path from C0 to Cα+1 in O(α2 + α√log C) time for a network N with a node and O(α2) arcs and nonnegative integer arc costs bounded by C.
There is another important result regarding weights of P∗ and weight of D∗.
Lemma-9. The weight of P∗ is equal to the weight of D∗ i.e., (P∗) = (D∗).
Proof. From the definition of (D∗), we must have
(D∗) = {(D): D is set of mutually disjoint cliques of G}.
Each set D of maximal mutually disjoint cliques forms a path P from C0 to Cα+1. From definition of the weight of path and weight of maximal disjoint cliques, we see that weight of any path P is the weight of the corresponding set of disjoint cliques D, i.e., w(P) = W(D). Hence, if Dλ corresponds to Pλ, (λ = 1, 2, … ,ℎ) then W(Dλ) = w(Pλ), for all λ = 1, 2, … , ℎ. Therefore, w(P∗) = max{w(P1), w(P2), … , w(Pℎ)} = max{W(D1), W(D2), … , W(Dℎ)} = W(D∗). Hence the result.
The Algorithm And Its Complexity
The major steps of the proposed sequential algorithm are listed below:
Algorithm DC
Input: An interval graph G with its interval representation.
Output: A maximum weight disjoint clique’s D∗.
Step-1: Compute all maximal cliques Ci, i = 1, 2,. . . , α with C0 = Φ = Cα+1
Step-2: Construct a network N.
Step-3: Compute a maximum weighted path PV∗.
Step-4: Identify all the cliques from the path PV∗ and put them to the set D∗.
end FD
The complexity of Algorithm DC is given blow:
Theorem-2: The maximum disjoint cliques of an interval graph G can be computed in (n2) time in sequential, where n is the total number of vertices.
Proof: Step-1 of the Algorithm DC can be computed in (n + γ) time, where γ is the sum of cardinalities of all cliques which is known and to be (n + m) time, where m is the number of edges of the graph [7]. Running time of Step-2 is of (α2) where α = (n) (Lemma-5). By Lemma-8, Step-3 takes (α2) time for implementation. Also, Step-4 takes (α2) time.
Therefore, overall time complexity of the Algorithm DC is of (n2). Hence the theorem.
Parallel Implementation and its Complexity
The steps of parallel algorithm are exactly same as sequential algorithm. The parallel implementation of each step of Algorithm DC is described in this section.Using the algorithm of Pal et al. [24-26], we can compute all maximal cliques of the interval graph, in parallel, 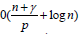 time using p processors on an EREW PRAM where γ is the output size and n is the number of vertices of the interval graph. Thus, Step-1 can be carried out
time using p processors on an EREW PRAM where γ is the output size and n is the number of vertices of the interval graph. Thus, Step-1 can be carried out 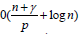 time using p processors on an EREW PRAM. The algorithm is optimal if
time using p processors on an EREW PRAM. The algorithm is optimal if
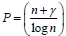 For an interval graph γ = (n + m) [20].A network N corresponding to an interval graph G can be constructed in (1) time using (α2) processors on an EREW PRAM, where α is the total number of maximal cliques of G.
For an interval graph γ = (n + m) [20].A network N corresponding to an interval graph G can be constructed in (1) time using (α2) processors on an EREW PRAM, where α is the total number of maximal cliques of G.
Maximum weighted path in N of G can be computed in (log2 n) time with 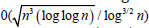 processors on an EREW PRAM model and in O(log n) time using O(n3+ε ), ε > 0 processors on a CREW model [21]. Hence, Step-3 and Step-4 requires same time.
processors on an EREW PRAM model and in O(log n) time using O(n3+ε ), ε > 0 processors on a CREW model [21]. Hence, Step-3 and Step-4 requires same time.
Therefore, all the steps of Algorithm DC can be performed in O(log2n) time with0( n3 (log log n) / log3/2 n) processors on an EREW PRAM model and in O(log n) time using O(n3+ε ), ε > 0 processors on a CREW model.
Thus, we have the following theorem:
Theorem-3. All disjoint cliques of an interval graph with n vertices can be compute in O(log2 n) time with processors on an EREW PRAM model and in O(log n) time using O(n3+ε), ε > 0 processors on a CREW model.
Concluding Remarks
In this paper, an efficient algorithm is designed to solve the disjoint cliques problem on interval graphs. The time complexity of the sequential algorithm is (n2) time where n is the number of vertices of the graph. A parallel algorithm is also designed. The time complexity of the parallel algorithm is of (log2n) time with  processors on an EREW PRAM model and (log n) time with (n3+ ), ε > 0 processors on a CREW PRAM model. It may be mentioned that the DAG approach has been used to design this algorithm. It may be noted that our proposed algorithm is not cost optimal but efficient. So, a new technique is required to solve this problem in sequential as well as parallel. [22-26]
processors on an EREW PRAM model and (log n) time with (n3+ ), ε > 0 processors on a CREW PRAM model. It may be mentioned that the DAG approach has been used to design this algorithm. It may be noted that our proposed algorithm is not cost optimal but efficient. So, a new technique is required to solve this problem in sequential as well as parallel. [22-26]
Acknowledgements
The author thankful to the anonymous referees for their valuable remarks which led to improvement of this paper I would like to acknowledge the Department of Higher Education, Science & Technology and Biotechnology, Govt. of West Bengal, India (245(Sanc.)/ST/P/S&T/16G-20/2017 dt.25/3/2018) for providing financial support during the project work. Also, I would like to thank my Research Guides, the Principal, all my colleagues and Research Scholar for their encouragement throughout this work.
REFERENCES
- Golumbic MC. Algorithmic graph theory and perfect graphs, Academic Press, New York.2000.
- Mishra LN. On existence and behavior of solutions to some nonlinear integral equations with Applications, Ph.D.Thesis, National Institute of Technology, Silchar788010, Assam, India. 2017.
- Mishra VN. Some problems on approximations of functions in banach spaces, Ph.D. Thesis, Indian Institute of Technology, Roorkee 247 667, Uttarakhand, India. 2007.
- Mishra VN, Mishra LN. Trigonometric Approximation of Signals (Functions) in Lp (p≥ 1)−norm. Int J Contemp Math Sciences. 2012;7:909- 18.
- Mishra VN, Delen S, Cangul IN. Algebraic structure of graph operations in terms of degree sequences. Int J Anal Appl. 2018; 16:809-21.
- Mishra VN, Delen S, Cangul IN. Degree sequences of join and corona products of graphs. Electronic J Math Anal Appl. 2019;7:5-13.
- Mondal S, Bera D, Pal M, et al. An optimal parallel algorithm for computing cut vertices and blocks on interval graphs. Intern J Computer Math. 2000;75:59-70.
- Jungck JR, Dick O, Dick AG. Computer assisted sequencing, interval graphs and molecular evolution. Biosystem. 1982;15:259-73.
- Fabri J. Automatic Storage Optimization. UMI Press Ann Arbor, MI.1982.
- Ohtsuki T, Mori H, Khu ES, et al. One dimensional logic gate assignment and interval graph, IEEE Trans. Circuits and Systems.1979;26: 675-84.
- Carlisle MC, Loyd EL. On the k −coloring of intervals, LNCS,497, ICCI’91.1991: 90-101.
- Hashimoto A, Stevens J. Wire routing by optimizing channel assignment within large apertures, Proc., 8th IEEE Design Automation Workshop. 1971:155-69.
- Johnson DS. The NP-completeness column: an ongoing guide. Journal of Algorithms.1985; 6:434-51.
- Frank A. On chain and antichain families of partially ordered sets. J Combinatorial Theory. 1980;29:176-84.
- Gavril F, Yannakakis M. The maximum k-colorable subgraph problem for chordal graphs. Information Processing Letters.1987;24:133-7.
- Jansen K, Scheffier P, Woeginger G. The disjoint cliques problem, Technical Report,Universitӓt Trier Mather Mathematk/Informatik, Forschungsbematk/Informatik, Forschungsbericht Nr. 1992:92-23.
- Mondal S, Pramanik T, Pal M. The diameter of an interval graph is twice of its radius. World Academy of Science, Engineering and Technology. 2011;80:1363-8.
- Gilmore PC, Hoffman AJ.A characterization of comparability graphs and of interval graphs. Canad J Math. 1964;16:539-48.
- Ahuja RK, Mehlhorn K, Orlin JB, et al. Faster algorithm for the shortest path problem. J ACM. 1990;37:213-23.
- Golumbic MC. Algorithmic graph theory and perfect graph. Academic Press, New York. 2000.
- Takoka T. A new upper bound on the complexity of the all-pair shortest path problem, Information Processing Letters. 1992;43:195-9.
- Mondal S, Pramanik T, Pal M. Minimum 2-tuple dominating set of an interval graph. International Journal of Combinatorics. 2011;14.
- Mondal S, Jana B, Pal M. Computation of the Inverse 1-center Location Problem on the Weighted Interval Graphs. Int J Computing and Mathematics. 2017.
- Pal M, Bhattacharjee GP. Optimal sequential and parallel algorithm for computing the diameter and the centre of an interval graphs. Intern J Computer Maths. 1995;59:1-13.
- Pal M, Bhattacharjee GP. The parallel algorithm for determining edge-packing and efficient edge dominating sets in interval graphs. Parallel Algorithms and Applications. 1995;7:193-207.
- Pal M, Bhattacharjee GP. An optimal parallel algorithm for computing all maximal cliques of an interval graph and its applications. J of Institution of Engineers. 1995;76:29-33.