A solvable sextic equation

Received: 02-Dec-2023, Manuscript No. puljpam-23-6666; Editor assigned: 03-Jan-2024, Pre QC No. puljpam-23-6666 (PQ); Accepted Date: Mar 28, 2024; Reviewed: 05-Jan-2024 QC No. puljpam-23-6666 (Q); Revised: 07-Jan-2024, Manuscript No. puljpam-23-6666 (R); Published: 31-Mar-2024, DOI: 10.37532/27528081.24.8(2).01-04

Citation: Yoon TC. A solvable sextic equation. J Pure Appl Math. 2024; 8(2):01-04.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

This paper presents a solvable sextic equation under the condition that several coefficients of such polynomials are restricted to become dependent on the preceding or following coefficients. We can solve a sextic equation by restricting one or two in total seven coefficients available, and by solving a bisextic equation and a quintic equation. And we can also find the arbitrary coupling coefficients that generate a new solvable sextic equation as well.

Key Words

De Moivre's theorem; Quintic equation; Sextic equation; Bisextic equation

Introduction

One of the solvable sextic equations is the de Moivre's sextic that comes from de Moivre's theorem, which is given as follows:

A solvable sextic equation

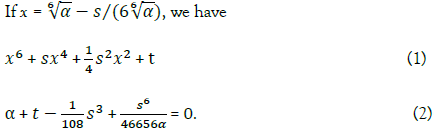
From (2), we get

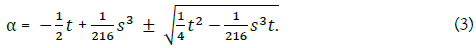
With this, we get the solution of the de Moivre sextic,

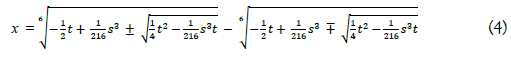
where one of ± in the left side square root changes to the opposite sign on the right side alternately. The solution of the de Moivre's sextic equation does not guarantee that all radicals of the sextic equation can be found [1-4].

The other one is

This sextic provides a solution

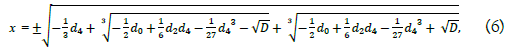
where D represents the discriminant,

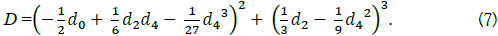
There is no solvable sextic equation in general, with the exceptions of the above including x⁶ + c₃x³ + c₀ = 0. There are three ways tofactor a sextic equation to derive a solution by splitting the sextic equation into lower polynomials.

One of them is a sextic equation factored by two cubics,

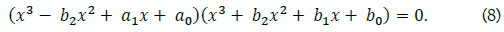
The other solution is a sextic equation factored into a quartic and a quadratic, i.e.,

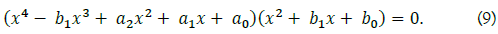
We can get solutions of the sextic equation factorized to a cubic equation as well as a quadratic factor of the above factorization.

A solvable sextic equation factored by two cubics

A solvable sextic equation factored by two cubic equations may be written as follows;

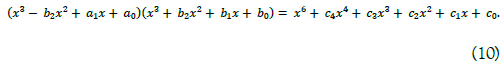
After eliminating the coefficients ai then b0 becomes

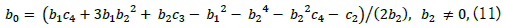
and, we get the following two simultaneous equations with respect to b₁,

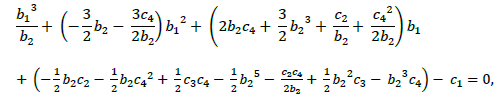
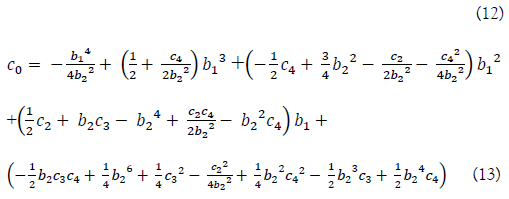
From the equation (12), we get a solution of b_1 after manipulation as follows

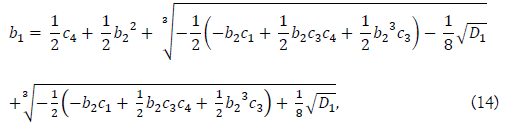
where D₁ is given as the discriminant of the cubic equation,

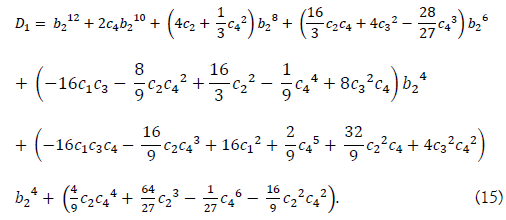
Though this equation with respect to b₂ is a 12^th degree equation, it can be solved using a sextic equation. An equation that can be solved by a sextic equation among 12^th degree equations may be called a bisextic equation.

A solvable sextic equation factored by a quadratic equation

Another solvable sextic equation may be given using the factors of a quartic equation and a quadratic equation as follows,

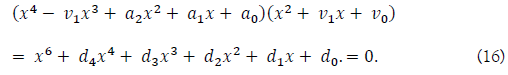
Developing the above, we get

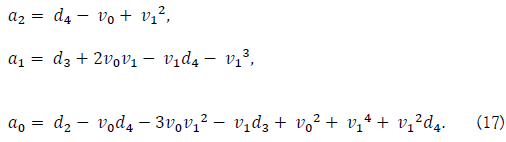
Plugging the above coefficients, we have

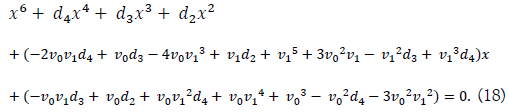
This sextic equation has a quadratic factor

From (18), we have two simultaneous equations with respect to v₁,

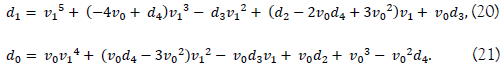
By using the equation (20), we may get a solution of a quintic by the use of the de Moivre's quintic equation as follows with two conditions that the coefficient d₃ = 0 of v₁² term and the two coefficients of v₁³ term and v₁ term are equal to each other. That is, the square of the former is equal to 5 times of the latter as in the de Moivre's quintic, and the coefficient d₀ of (21) dependent on the preceding coefficients of the sextic equation,

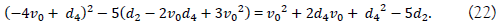
From (22), we have

then the equation (20) provides

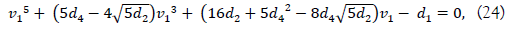
and we have a solution of v₁

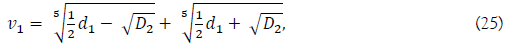
where, D₂ is the discriminant of the resolvent quintic (20),

The sextic equation (16) has a quadratic factor

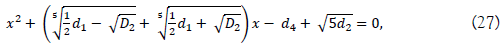
with D₂ of (26).

From (27), we have two roots, which are the two radicals of the sextic equation (16)

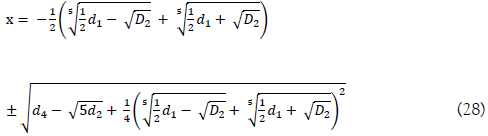
This process is also one of the ways to find the conditional solution of a sextic equation.

Derivation of a solvable sextic equation factored by two cubic equations

For solving a bisextic equation, replace b₂² in the discriminant D₁ of (15) with y, and after reducing the coefficient of y⁵ term by b₂²= y - c₄/3, we have

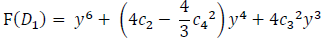
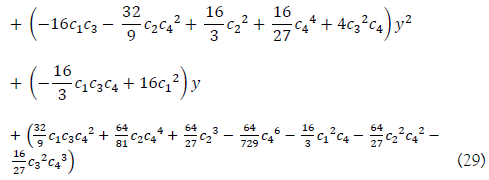
If F(D₁) has a quadratic factor, (y₂ + v₁y +v₀), then we get byusing the equation (20),

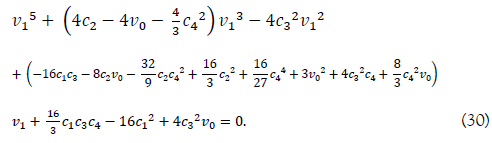
If the above quintic equation is to be a de Moivre's quintic, we can solve the quintic. In order to do so, the coefficient c₃ of v₁² term isequal to zero, and the square of the coefficient of v₁³ term is equal to five times the coefficient of v₁ term.

With these conditions, we have

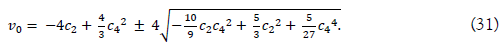
And we get v₁,

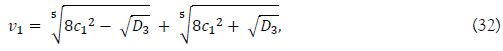
where D₃ represents

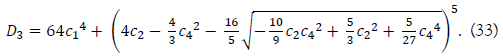
From the quadratic factor of the equation (29), we get two roots of the sextic

With the result, b₂ of (15) is given as follows;

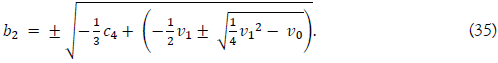
Now, we can get a solution of a sextic equation by solving the cubic factors x³ + b₂x² + b₁x + b₀ of (10), by using b₂ of (35), b₁ of (14) with the discriminant D₁ of (15), and b₀ of (11).

Writing down the solution of x in a row as a single equation is too lengthy and difficult to distinguish at a glance, so it would be more convenient to arrange each variable separately.

In the case of trying to get a solvable sextic equation that can be determined to be solved by applying arbitrary coefficients, b₂, b₁ and D₁, the constant coefficient c₀ of (13) may return a different value other than expected.

Example # 1

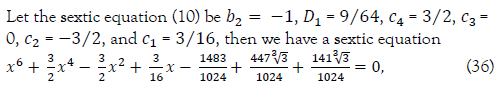
which has two cubic factors

Example # 2

Let b₂ = 1, c₄ = -3, c₃ = 0, c₂ = 3, and c₁ = 4, then we get D₁ = 256 and 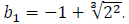The sextic equation becomes

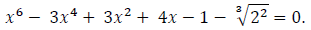
And two cubic factors are

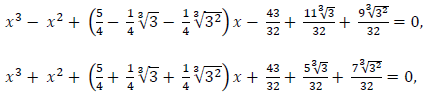
Example # 3

Let b₂ = 1, c₄ = 0, c₃ = 0, c₂ = -3/4, and c₁ = 1/4, then D₁ = 1, and we get

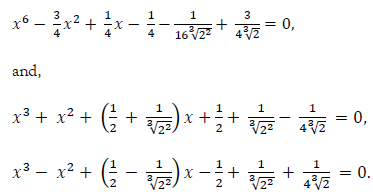
and,

Example # 4

From the equation (16) and (28), let d₄ = 0, d₃ = 0, d₂ = 5, d₁ = 64, then D₂ = 0, and the equation becomes

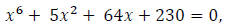
and the quadratic factor provides

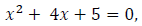
Factoring a sextic equation into two cubic equations

Another one is directly factoring a sextic equation into two cubic equations. For this, we may apply the following formula, which has the form of A² - B² = (A - B)(A + B),

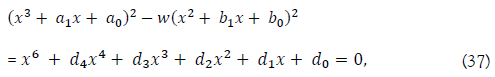
where w is a coupling constant.

This result is also the same as the cases mentioned above, but when w is less than 0, it becomes an imaginary number, and the sextic equation would have all 6 imaginary roots.

Example # 5

Let coefficients of the sextic equation (36) be b₁ = -3/2, d₄ = -12, d₃ = 0, d₂ = 0, and d₁ = 1953/32, then we have w = 5/2, b₀= 271/80,and d₀ = −37441/2560 Therefore, the sextic equation becomes

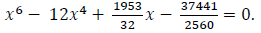
This sextic equation has two cubic factors as

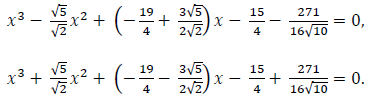
References

1.Sextic_equation

2.Cayley's sextic

3.Kulkarni RG. Solving sextic equations

4.Hagedorn T.R. General formulas for Solving Solvable SexticEquations.