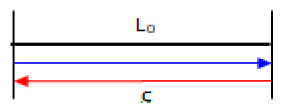A Study on the Absolute Stationary Inertial Frame and the Inertia Mass, Momentum and Kinetic Energy in the Inertial Frame moving relative to it.

Received: 14-Jan-2023, Manuscript No. puljpam-23-6171; Editor assigned: 16-Jan-2023, Pre QC No. puljpam-23-6171 (PQ); Accepted Date: Jan 27, 2023; Reviewed: 17-Jan-2023 QC No. puljpam-23-6171 (Q); Revised: 18-Jan-2023, Manuscript No. puljpam-23-6171 (R); Published: 30-Jan-2023, DOI: 10.37532/2752-8081.23.7(2).45-52

Citation: Mok J. A study on the absolute stationary inertial frame and the inertia mass, momentum and kinetic energy in the inertial frame moving relative to it. J Pure Appl Math. 2023; 7(2):45-52.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

Assuming that an absolute stationary inertial frame exists in the universe and the speed of light is constant only in the absolute stationary inertial frame, new equations for inertial mass, momentum and kinetic energy in a moving inertial frame are derived.

In the process of deriving the new equations, an experiment was presented to obtain the velocity of the inertial frame moving relative to the absolute stationary inertial frame. If this experiment is successful, we could find out how fast and in which direction our Earth is moving in space.

Keywords

Special Relativity; Speed of Light; Kinetic Energy; Inertial Mass; Relativity Velocity; Absolute Stationary Inertial Frame

Introduction

The Albert Einstein derived the equations for time dilation, mass increase, and kinetic energy in the theory of special relativity published in 1905, assuming that light speed is constant in all inertial frames and the absolute stationary inertial frame does not exist in the universe [1].

In this study, new equations for inertial mass, momentum, and kinetic energy in an inertial frame moving relative to the absolute stationary inertial frame are derived by assuming that an absolute stationary inertial frame exists and using the two assumptions for the speed of light below.

• Assumption 1: An absolute stationary inertial frameexists in the universe

• Assumption 2: The speed of light observed in anabsolute stationary inertia frame is constant regardless ofthe movement of the light source. That is, light emittedfrom both a moving and a stationary object have thesame speed in an absolute stationary inertial frame.

• Assumption 3: Based on Michelson-Morley’s experiment [2], in a moving inertial frame, the round-trip speed oflight in all directions is the same and is equal to thespeed of light in the absolute stationary inertial frame.

Conversion factors to absolute stationary inertial frame

As shown in Figure 1, in order to calculate the kinetic energy of an object thrown from a moving inertial frame in terms of an absolute stationary inertial frame, the following four conversion factors are used.

Figure 1: Observe a golf ball hit in an inertial frame flying with velocity v₀ in an absolute stationary inertial frame

• Length conversion factor

• Time conversion factor

• Velocity conversion factor

• Mass conversion factor

In the process of deriving this equation, an experiment is presented to determine the velocity of an inertial frame moving relative to the absolute stationary inertial frame and the new equation for the relative velocity of an object observed in a moving inertial frame to the absolute stationary inertial frame [3-10].

Factor that converts length observed in the moving inertial frame to length observed in the absolute stationary inertial frame

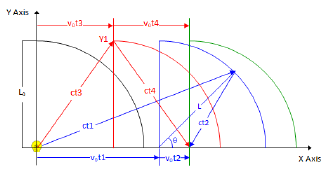
As shown in Figure 2, consider that a spacecraft with a semicircular reflector flies at v₀ speed and generates light at the center of the spacecraft.

Figure 2: A spaceship flying at velocity v₀ relative to the absolute stationary inertia frame

The path of light emitted from the source at the center of the spaceship hits point Y1. Point Y1 reflects the light back to the source. The motion of this light path is observed from the absolute stationary inertial frame as follows in Figure 3:

Figure 3: The path of light in a spacecraft observed in an absolute stationary inertial frame

The path of light reflected at point Y1 and returned to the center of the spaceship

Assuming no length contraction in the Y axis, the time t3+t4, represents the time it takes for the emitted light to hit Y1 point and reflect back to the source. The time t3+t4 can be calculated as follows in the absolute stationary inertial frame.

t3: The time it takes for the light emitted from the source at center of the spaceship to reach point Y1 of the reflector.

t4: The time it takes for the light reflected from point Y1 back to the center of the spaceship.

The path of light reflected from a point on the reflector and returned to the center of the spaceship

The time t1+t2, represents the time it takes for the emitted light to travel from the source at center of the spaceship to any point on the reflector, then back to the source. This can be calculated for the absolute stationary inertial frame as follows:

Based on Assumption 3, the speed of light is the same in all directions, so the time for the round-trip t1+t2, Equation (4), for any one point, and time for the round-trip t3+t4, Equation (1), for Y1, must be the same.

Hence,

The length L0 in a moving inertial frame is observed to be contracted compared to L in the absolute stationary inertial frame a follows:

The length contraction factor R_L that converts length in a moving inertial frame to length in the absolute stationary inertial frame is defined as follows:

Factor that converts time observed in the moving inertial frame to time observed in the absolute stationary inertial frame

In a moving inertial frame, unit time is defined as the time for light to travel a distance L₀ back and forth as shown in Figure 4.

Figure 4: Unit time in an inertial frame

Unit time in an inertial frame is expressed as follows:

Since the absolute stationary inertial frame observes the round-trip time of the moving inertial frame as Equation (1) that is always greater than time of Equation (7), it can be inferred that the unit time in the moving inertial frame is slower than the unit time in the absolute stationary inertial frame.

Using the absolute stationary inertial frame time t as Equation (1) and the moving inertial system time t0 as Equation (7), the factor R_T that converts the moving inertial frame time to the absolute stationary inertial frame time is defined as follows;

How to measure the velocity, V₀ of a moving inertial frame

Based on Equations (2) and (3), the difference between the time t1 to reach a surface point and the time t2 to return to the source can be expressed as follows in the absolute stationary inertial frame:

Considering time dilation, the time difference in a moving inertial frame is then

If the maximum Δt_s_max can be measured by experiment, the velocity of the moving inertial frame can be obtained as follows:

If this experiment is successful, one can determine the direction and velocity of the inertial frame moving in space.

Factor that converts the velocity observed in the moving inertial frame to the velocity observed in the absolute stationary inertial frame

Using the length conversion factor R_L, Equation (6), and the time conversion factor R_T, Equation (8), the factor R_v can then be derived. R_v is the factor that converts the observed velocity in the moving inertial frame to the velocity observed in the absolute stationary inertial frame:

Relative velocity of an object observed in a moving inertial frame to the absolute stationary inertial frame

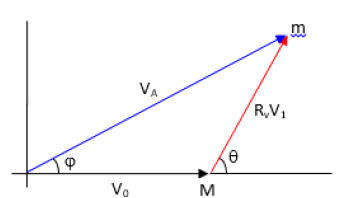
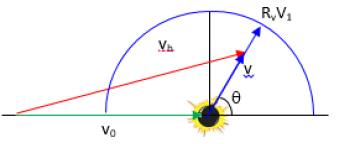
When a moving object is observed as v_A in an absolute stationary inertial frame and v₁ in an inertial frame moving with a velocity v₀, the velocity v₁ in the moving inertial frame is observed as R_v v₁ in the absolute stationary frame, so these velocities can be expressed as shown in Figure 5.

Figure 5: Schematic relationship between velocity V_A and the direction j observed in the absolute stationary inertial frame, and velocity V₁ and direction q observed in an inertial frame moving at velocity V₀

Based on , the relationship between ν_A and ν₁ can be shown as follows:

Based on the Equations, the relative velocity ν₁ and θ can be expressed by ν₀, ν_A and φ as follows:

The absolute velocity ν_A can be expressed by ν₁ and ν₀ as follows;

Since the velocity ν_A observed in an absolutely stationary inertial frame cannot exceed the speed of light, c, the maximum value of ν₁ can be obtained by substituting ν_A = C in Equation is as follows:

Equation defines the maximum velocity of an object that can be observed or created in an inertial frame moving at velocity ν₀.

This is also consistent with the result obtained from kinetic energy Equation (39).

At θ = 0,θ = π / 2,θ = π , Equation can be simply expressed as follows:

Between 0 < θ < 2π, the average value of v_{1_max} , v_{1_ ave _max} is obtained by dividing the circumference of a circle with a unit radius; that is, 2π by the time required for circular motion. The time it takes to go around the circle is obtained by integrating the time to travel a unit distance with over the interval 0 < θ < 2π

Equation (21) indicates that the circular motion speed of an object in a moving inertial system cannot exceed the speed c of light.

Suppose we observe the forward light, that is, the light in the direction , from a spaceship moving at the speed of light.

When v₀ is close to c, Equation (19) converges to c/2 for the direction of

That is, the forward light in an inertial frame moving at the speed of light (v₀=c) is observed as c/2.

Mass increase due to a moving inertial velocity

When a bomb with at-rest mass m₀ in the absolute stationary inertial frame flies at a speed of v₀ and explodes at a speed v₁, that is relatively much slower than the speed of light in all directions as shown in Figure 6.

Figure 6: A bomb with at-rest mass m₀ explodes with velocity v1 while flying with velocity v₀

This explosive kinetic energy is assumed as follows considering the mass increase factor, γ:

Where, γ₀: the mass increase factor γ at the velocity of the moving inertial frame, v₀

As shown in Figure 7, the velocity v_b of the fragment observed in the absolute stationary inertial frame can be expressed as follows:

Figure 7: The velocity of an object of mass m thrown at velocity V₁ in an inertial frame of mass M, and the change in velocity of an inertial frame of mass M observed in an absolute stationary frame.

The mass increase factor γ is inferred using the following two approaches.

Approach 1

Assume that the mass increase factor γ due to the velocity of a moving inertial frame is as follows:

If ν₁ is relatively close to 0 compared to the speed of light, the fragment kinetic energy in an arbitrary direction observed in the absolute stationary inertial frame can be calculated by an approximate equation below:

Equation (26) can be simplified as follows when v₁ is close to 0:

The total explosive energy of the bomb can be obtained as follows by integrating Equation (27) for all three-dimensional directions.

In Equation (28), 1/2 is the only value of n that satisfies Equation (23), so γ can be estimated as follows;

Approach 2

If ν₁ is relatively close to 0 compared to the speed of light, the fragment kinetic energy in an arbitrary direction observed in the absolute stationary inertial frame can be expressed as an approximate equation using the mass increase factors γ₀ and γ₁ as:

Where

γ₀: the mass increase factor γ at the velocity of the moving inertial frame, v₀

γ₁: the mass increase factor γ at square root of the average of v_b²

Average of

The total explosive energy of the bomb can be obtained as follows by integrating Equation (30) for all three-dimensional directions.

Since Equation (32) must satisfy equation (23),

Based on (33), assuming and calculating in (34), it proves the assumed correct:

Kinetic energy, momentum and inertial mass in an inertial frame moving relative to an absolutely stationary inertial frame

Kinetic Energy Observed in Absolute Stationary Inertial Frame

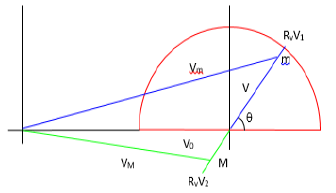
As shown in , an object with mass m is thrown at velocity ν₁ and angle θ in an inertial frame with mass M moving with velocity ν₀.

Observing this in the absolute frame, the object with mass m moves to R_vv₁ due to the velocity conversion factor R_v, Reference source not found., and the inertial frame with mass M moves in the opposite direction at velocity.

Therefore, the velocities of m and M observed in the absolute stationary inertial frame can be expressed as:

Using the mass increase factor γ from Equation, m and M are expressed as follows;

Using Equations, (35) to (38), the kinetic energy observed in the absolute stationary inertial frame can be calculated as follows:

Momentum observed in moving inertial frame

The moving inertial kinetic energy, E_KS , can be calculated with the momentum, P_s, and velocity, ν, as follows:

Since the kinetic energy, E_Ka , calculated in the absolute stationary inertial frame, and the kinetic energy, E_KS , calculated in the moving inertial frame must be the same,d(P_s) can be obtained by differentiating Equations as follows:

The momentum in the moving inertial frame can be obtained by integrating d(P_s), Equation (41), as follows:

Inertial mass in a moving inertial frame

Using the momentum Equation (42) in the moving inertial frame, the inertial mass in the moving inertial frame can be obtained as follows:

Based on (43), the inertial mass is a function of the velocity of the inertial frame and direction.

Conclusion

The conclusion of this study and the difference from the theory of special relativity are as follows:

	Theory of Special Relativity	Conclusion of this study
Absolute Stationary Inertial Frame	None	Exists
Constancy of Light Speed	Constant in all inertial frames	Constant only in the absolute stationary inertial frame. In a moving inertial frame, the round-trip speed of light is constant
Velocity of a moving inertial frame	No way to measure
Speed of light observed in a spaceship flying at the speed of light	C
Momentum
Kinetic Energy
Inertial Mass

References

1. A. Einstein. On The Electrodynamics of moving bodies. 1905:.1-24

   [Crossref]

2. Michelson-Morley Experiments. 1887

   [Crossref]

3. Bai X, Yao D, Du Y, et al. Derivation of Digital-to-Analog Converter Architectures Based on Number Theory. J Pure Appl Math. 2022; 6(5):14-24.

   [Google Scholar] [Crossref]

4. Jasani DS. Assessing anxiety and attitudes towards arithmetic and algebra. J Pure Appl Math. 2022; 6(5):01-11

   [Google Scholar] [Crossref]

5. Luong TT, Cuong NN, Giang TTN, et al. Enhancing Security ofAES Block Cipher Via Key-Dependent Dynamic XOR Tables. J Pure Appl Math. 2022; 6(5):25-31

   [Google Scholar] [Crossref]

6. World Health Organization, Sexually transmitted infections (STIs). 2021 [Crossref]
7. China's National Bureau of Statistics, China Statistical Yearbook. (2021).
8. Garnett GP, Aral SO, Hoyle DV, et al. The natural history of syphilis: implications for the transition dynamics and control of infection. J Sex Transm Dis. 1997;24(4):185–200

   [Google Scholar] [Crossref]

9. Grassly C, Fraser C, Garnett G P. Host immunity and synchronized epidemics of syphilis across the United States. J Nature. 2005; 433:417-21

   [Google Scholar] [Crossref]

10. Tuite A, Fisman D. Go big or go home: impact of screening coverage on syphilis infection dynamics. J Sex Transm Infect. 2016; 92:49-54

    [Google Scholar] [Crossref]