A very elementary proof of an explicit formula of Bernoulli Numbers
Received: 04-May-2024, Manuscript No. puljpam-24-7045; Editor assigned: 05-May-2024, Pre QC No. puljpam-24-7045(PQ); Accepted Date: May 27, 2024; Reviewed: 06-May-2024 QC No. puljpam-24-7045(Q); Revised: 08-May-2024, Manuscript No. puljpam-24-7045(R); Published: 31-May-2024, DOI: 10.37532/2752- 8081.24.8(3).01-04
Citation: Benmoussa A. A very elementary proof of an explicit formula of Bernoulli Numbers. J Pure Appl Math. 2024; 8(3):01-04.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
The aim of this paper is to give an easy and very elementary proof of a well-known explicit formula for Bernoulli numbers.
Key Words
Stirling numbers of the second kind; Bernoulli numbers; Bernoulli polynomials
Introduction
The numbers :
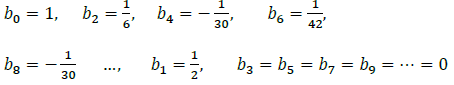
are called the Bernoulli numbers. They can be defined by the following exponential generating function:
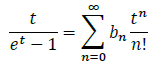
When this sequence of numbers appeared in 1713, mathematicians didn’t know a formula to compute bn directly, so they used recursive formulas like this one [1]:
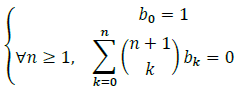
In 1883, Worpitzky gave the following formula for bn [2]:
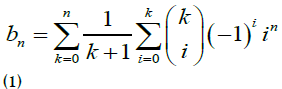
We can also find other mathematicians from the 19th century who proved formula (1), such as Cesàro in 1885 and d’Ocagne in 1889 [3, 4].
For our part, we present here an elementary proof of the formula (1).
Stirling Numbers of the Second Kind
Let Y be an arbitrary function and set:
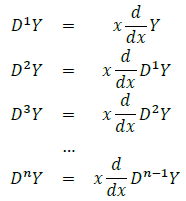
If we develop the first four functions, we find:
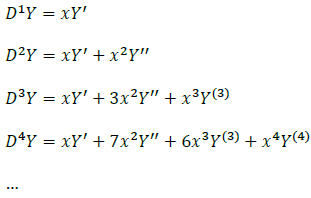
We conjecture that:
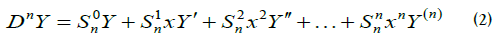
The coefficients 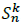 are called Stirling numbers of the second kind.They can be represented in a triangle similar to Pascal’s triangle. The triangle of the numbers
are called Stirling numbers of the second kind.They can be represented in a triangle similar to Pascal’s triangle. The triangle of the numbers 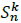 is the following:
is the following:
TABLE 1 The law for forming the numbers
| k=0 | k=1 | k=2 | k=3 | k=4 | … | |
|---|---|---|---|---|---|---|
| n=0 | 1 | |||||
| n=1 | 0 | 1 | ||||
| n=2 | 0 | 1 | 1 | |||
| n=3 | 0 | 1 | 3 | 1 | ||
| n=4 | 0 | 1 | 7 | 6 | 1 | |
| … | … | … | … | … | … | … |
We observe that:
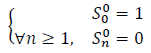
The law for forming the numbers in the above table is given by:
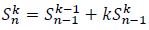
The Explicit Formula for Stirling Numbers of the second kind
If we put Y = ex in the formula (2), we obtain:
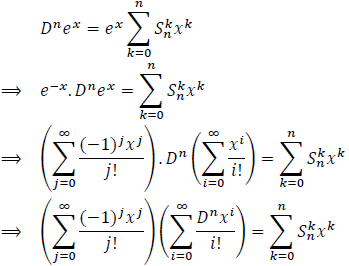
One can easily prove that Dnxi = inxi, so:
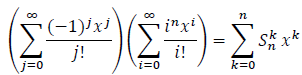
If we develop the left-hand side we obtain:
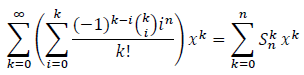
Comparing coefficients in both summations, we conclude that:
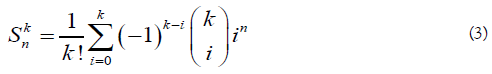
Relation between Bernoulli Numbers and Stirling Numbers of the Second Kind
Putting Y = xy in the formula (2), we get:
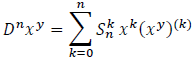
We know that (xy)(k) = y(y-1)...(y-k+1)xy-k and Dnxy = ynxy so we get:
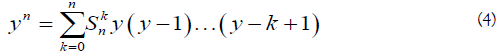
The polynomialy (y-1)...(y-k+1) is called the falling factorial of y of order k. Pochhammer used the symbol (yk) to denote it, so the formula (4) becomes using Pochhammer symbol:

One interesting property of the falling factorial function is the following:
Proposition
Let y,n be non-negative integers, then:
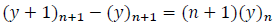
Proof
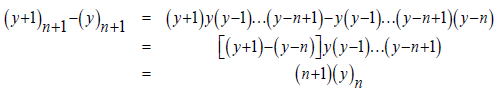
We are going to use this property in the proof of the following proposition.
Proposition
Let (n,m) ∈ℕ2. We have:
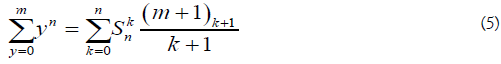
Proof
If we sum for y in the formula (4’) we find:
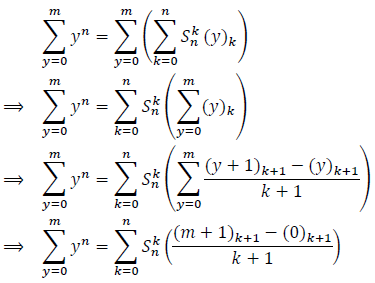
Therefore:
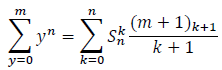
Definition
Let ∈ℕ
The Bernoulli polynomials Bn(x) are defined by the following generating function:
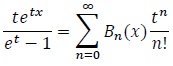
One interesting observation to make about Bernoulli polynomials is that if we put x=0 we get:
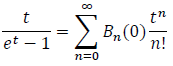
This generating function corresponds to the generating function of Bernoulli numbers bn. Hence for all n∈ℕ, we have:
Bn(0) =bn
Another interesting property of the Bernoulli polynomials is the following:
Proposition
Let n∈ℕ
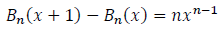
Proof
On the one hand:
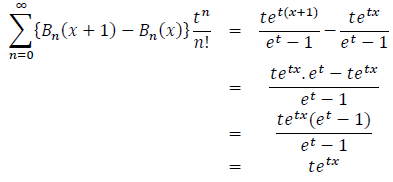
On the other hand:
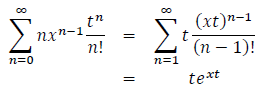
Comparing coefficients of both summations we conclude that:
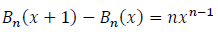
Proposition
Let n∈ℕ
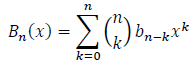
Proof
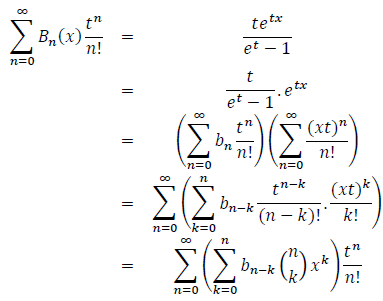
Therefore:
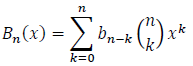
If we sum for y in the relation B(n+1)(y+1) - B(n+1)(y) = (n+1)yn, we obtain :
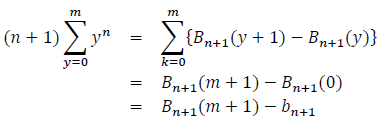
Thus:
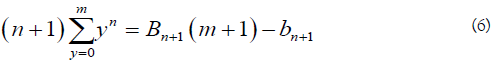
Comparing formula (5) with formula (6). We conclude that:
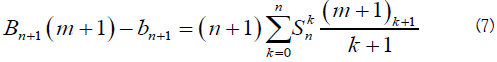
If we develop the expression of (X)k+1 in terms of the powers of X we find:
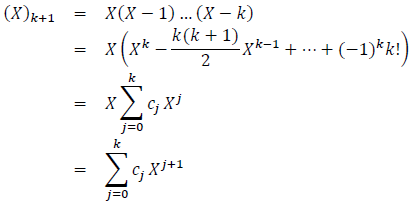
Therefore:
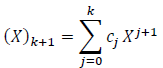
If we apply the above formula for (m+1)k+1 in the formula (7) we find:
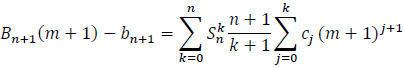
Substituting also Bn+1(m+1) by its explicit expression, we finally get:
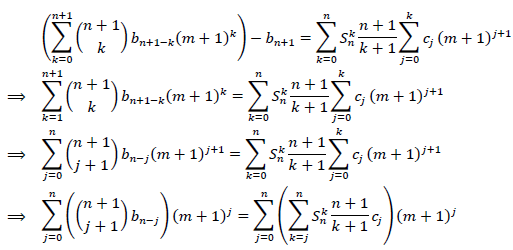
We have equality between two polynomials in m+1, both of degree n, so the coefficients of the terms of the same degree are equal. In particular for j = 0 we have:
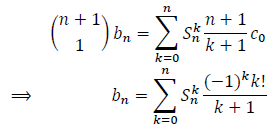
To get the explicit expression of bn in terms of n, we substitute 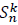 in the above identity by its explicit expression, and after simplification we obtain the remarkable formula (1) for the Bernoulli numbers.
in the above identity by its explicit expression, and after simplification we obtain the remarkable formula (1) for the Bernoulli numbers.
References
- Schneider I, Bernoulli J, Conjectandi ARS. InLandmark Writings in Western Mathematics. Elsevier. 1713; 88-104.
- J. Worpitzky, Studien uber die Bernoullischen und Eulerschen Zahlen. J Reine Angew Math. 1883;94:203-32.
- Cesàro E. Sur une équation aux différences mêlées. Nouvelles annales de mathématiques. J des candidats aux écoles polytechnique et normale. 1885;4:36-40.
- D'Ocagne M. Sur les nombres de Bernoulli. Bulletin de la Société Mathématique de France. 1889;17:107-9.






