Analytical solution of General Fisher’s Equation by using Laplace Adomian decomposition method

Received: 02-Nov-2018 Accepted Date: Nov 24, 2018; Published: 29-Nov-2018, DOI: 10.37532/2752-8081.18.2.9

Citation: Ali A, Humaira, Laila, et al.. Analytical solution of General Fisher’s Equation by using Laplace Adomian decomposition method. J Pur Appl Math. 2018;2(3): 01-4.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

In this paper, we use Laplace Adomian Decomposition Method (LADM) to solve a nonlinear Fisher’s partial differential equation (PDE). The adopted method is illustrated by solving two special cases of Fisher’s partial differential equation. This method is much reliable for its high convergence rate of approximate solutions to the exact solution.

Introduction

Nonlinear differential equations are too much important to us due to the fact that most of the physical phenomena are nonlinear in nature and which are described by these equations. Particularly partial differential equations play an important rule in this regard. In the last few decades several researchers have been made considerable e orts and adopted various approaches for the solution of nonlinear PDEs. Recently in [1], Arqub applied the reproducing kernel Hilbert space method and computational iterative method, in nding the approximate solutions for certain classes of Neumann time-fractional PDEs. In [2], the author studied the approximate solutions for certain classes of Robin timefractional PDEs via fitting the reproducing kernel algorithm. Similarly we refer to the work in [3,4]. Unfortunately most of the nonlinear problems cannot be solved by analytic methods. Moreover the traditional numerical methods need perturbation, discretization, linearization or transformation to solve the nonlinear problems. The Adomian decomposition method proved free of such steps and hence widely used in the literature, see [5]. Another important method which has gained much concern is the Laplace Adomian polynomial or decomposition method (LADM). It was introduced by Suheil A Khuri [6]. This method is actually a hybrid technique developed by the combination of the two well-known and powerful methods namely Laplace transform and Adomian decomposition method. Using this method one can and the numerical solutions without the restrictive assumptions and discretization and hence it is free from round o errors. Similarly using this method, a solution in the form of in finite series is obtained which has a highest and rapid convergence rate to the exact solution of the concerned problem. By adopting this method, the numerical computations can be reduced. The reliability of LADM and the reductions in computations show that LADM is widely applicable. In addition LADM involving simple and straightforward calculation. This method has applications to the Duffing, Bratu and other nonlinear equations as in [7,8]. In [9] Wazwaz et al. applied the combined Laplace-Adomian decomposition method for the solution of singular integral equation of heat transfer. In [10] Wazwaz applied the combined Laplace transform-Adomian decomposition method for the solution of nonlinear Volterra integro-di erential equations. In [11] Patel et al. applied Laplace Adomian Decomposition Method for the soliton solutions of Boussinesq-Burger equations. In this paper we apply the Laplace Adomian Decomposition method to the general Fisher’s equation and its two special types and obtain their series solutions.

Laplace adomian decomposition method and its application to general fisher’s equation

Consider the following general fisher equation

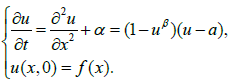
We take the operators Lu(x,t) = Ru(x,t) + Nu(x,t).

From which we represent Eq.(1) as

Lu(x,t) = Ru(x,t) + Nu(x,t).

Taking Laplace transform, we get

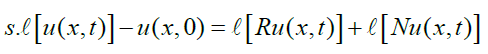
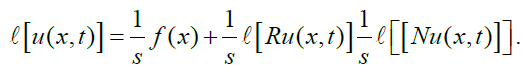(2)

Let

Where A_K is Adomian polynomial which is defined as

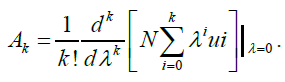
Then from Eq. (2), we have

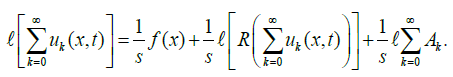(3)

Comparing terms on both sides, we have

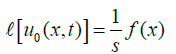
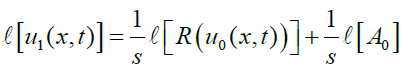
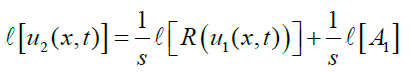
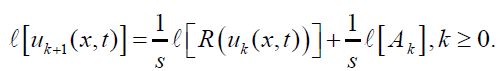(4)

Applying inverse Laplace transform, we get

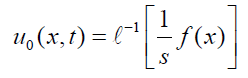
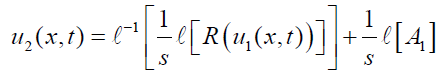
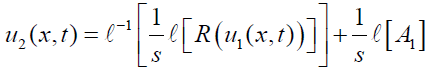
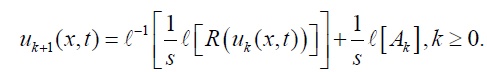
In this way computing inverse transform we get the solution in the form of infinite series as

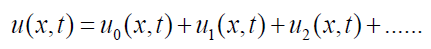(6)

Theorem 2.1. Convergence of the method:Suppose that ε is Banach space and T :ε →ε is a contraction non linear mapping and if we consider the generated sequence of solutions via LADM is written as

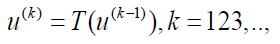
then the following holds

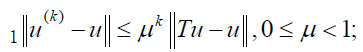
2u^{(k )} (x,t) is always hold in the neighborhood u(x,t) implies that

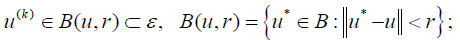
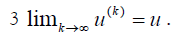
Proof. For proof see [12].

Examples

To demonstrate the applicability of LADM, we consider the following two particular examples of Fisher equations.

Example 3.1 Consider the Fisher equation (1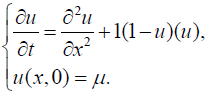7).

(7)

Comparing this problem with the general form of Fisher equation in (1), we see that α =1, a = 0 , a = 0 and f (x) = μ Applying Laplace transform to

Eq.(7), we get 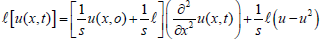(8)

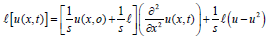By using initial condition, Eq. (8) becomes

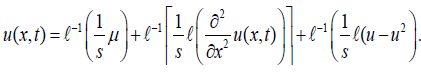
Applying inverse Laplace transform, we get

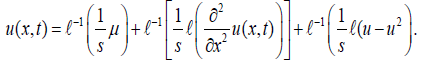(9)

The Laplace decomposition method assumes a series solution of the function u(x,t) is given by

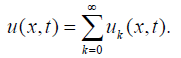(10)

Using Eq. (10) in Eq. (9), we obtain

(11)

In above equation A_K (u ) is Adomian polynomial which represents the nonlinear term. So Adomian polynomials are given below.

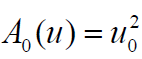
First few polynomials of the Adomian method are given as:

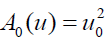
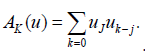
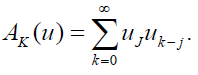
From (11), we get

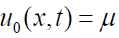
and the recursive relation:

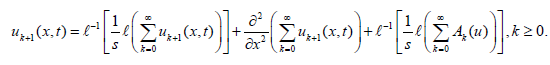
For k = 0; we get

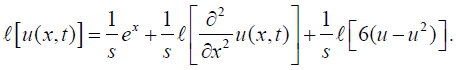
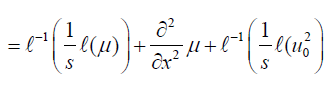
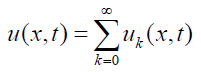
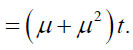
Therefore, the solution obtained by Laplace Adomian Method is given below

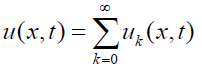
(12)

Using algebraic manipulation, we get the exact solution given by

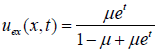which is same

as given by homotopy perturbation method (HPM) as given in [13].

Example 3.2.

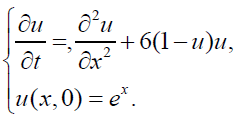
Here α = 6 ; a = 0 and a = 0 and the initial condition

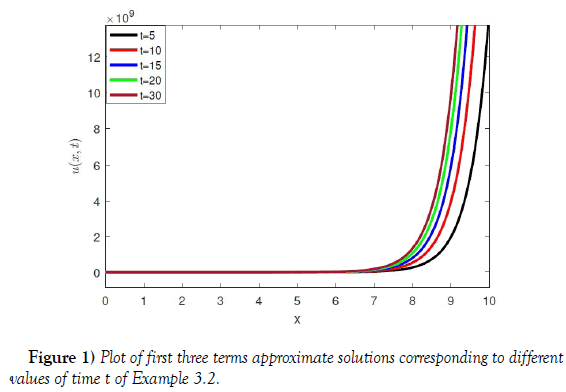
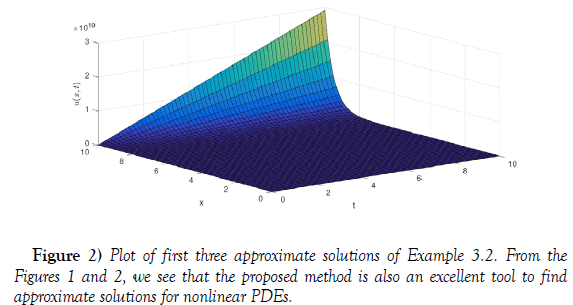
u(x,0) = e^x .Taking Laplace transform, we have (figure 1)

Figure 1) Plot of first three terms approximate solutions corresponding to different values of time t of Example 3.2.

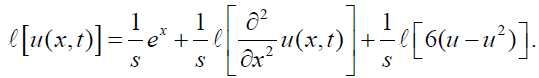
Applying the inverse Laplace transform, we get

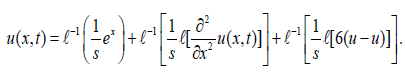(13)

Using Eq. (10) in Eq. (13), we obtain

(14)

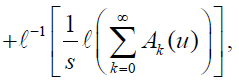(15)

Where A_K (u ) are Adomian polynomials few terms of the Adomian polynomials are given below

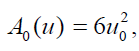
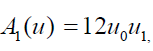
From (14), we get

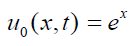
and the recursive relation is

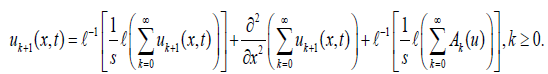
The few terms of uk(x,t) follow

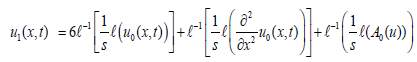
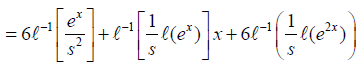
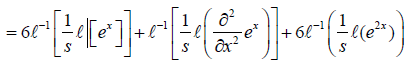
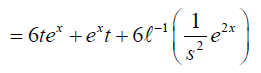
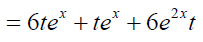
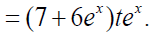
Similarly other terms can be computed. Therefore, the solution obtain by Laplace Adomian decomposition method is given below

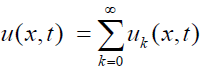
Which is the required solution. (figure 2)

Figure 2) Plot of first three approximate solutions of Example 3.2. From the Figures 1 and 2, we see that the proposed method is also an excellent tool to find approximate solutions for nonlinear PDEs.

Conclusion

Laplace Adomian decomposition method is an hybrid technique consisting of the two different concepts \Laplace transform and Adomian decomposition method”. This method has some advantages over the previously adopted methods. We can obtain the numerical solutions by this method without the restrictive assumptions and discretization. This method is free from round off errors and it has high convergence rate to the exact solution. In this paper, we have applied the Laplace Adomian decomposition method to general nonlinear Fisher’s partial differential equation; its two particular cases have been successfully handled for their series solutions.

Competing Interest

It is declared that no competing interest exists regarding this manuscript.

Acknowledgements

We are very thankful to the reviewers for their useful correction and suggestions.

REFERENCES

1. Arqub OA. Fitted reproducing kernel Hilbert space method for the solutions of some certain classes of time-fractional partial differential equations subject to initial and Neumann boundary conditions. Comp Math Appl. 2017;73(6):1243-61.
2. Arqub OA. Numerical solutions for the Robin time-fractional partial differential equations of heat and fluid flows based on the reproducing kernel algorithm. International Journal of Numerical Methods for Heat and Fluid Flow. 2018;28(4):828-56.
3. Arqub OA. The reproducing kernel algorithm for handling differential algebraic systems of ordinary differential equations. Math Meth in the App Sci. 2016;39(15):4549-62.
4. Arqub OA, Z Odibat, Mal Smadi. Numerical solutions of time-fractional partial integrodifferential equations of Robin functions types in Hilbert space with error bounds and error estimates. Nonlinear Dynamics. 2018;94(3):1819-34.
5. Adomian G. Solving frontier problems of physics: the decomposition method, Kluwer Academic, Dordrecht. 1994.
6. Khuri SA. A Laplace decomposition algorithm applied to a class of nonlinear differential equations. J Math Annl Appl. 2001;1(4):141-55.
7. Khuri SA. A new approach to Bratus problem, Appl. Math. Comp. 2004;47:31-136.
8. Hendi FA. Laplace Adomian decomposition method for solving the nonlinear volterra integral equation with weakly kernels, Studies in Nonlinear Sciences. 2011;2:129-34.
9. Wazwaz AM, MS Mehanna. The combined Laplace-Adomian method for handling singular integral equation of heat transfer. Inter J of Nonlinear Science. 2010;10:248-52.
10. Wazwaz AM. The combined Laplace transform-Adomian decomposition method for handling nonlinear Volterra integro-differential equations, Applied Mathematics and Computation. 2010;216(4):1304-9.
11. Patel HS, Meher R. Application of Laplace Adomian decomposition method for the soliton solutions of Boussinesq-Burger equations. Int J Adv Appl Math and Mech. 2015;3(2):50-8.
12. Shah K, Khalil H, Khan RA. Analytical solutions of fractional order diffusion equations by natural transform method. Iran Journal of Science and Technology. 2016:1-12.
13. Agirseven D, Ozis T. An analytical study for Fisher type equations by using homotopy perturbation method, Computers and Mathematics with Applications. 2010;60:602-9.

Keywords