Application of Graph Theory In Air-Transportation Network

Received: 17-Nov-2020 Accepted Date: Mar 10, 2021; Published: 17-Mar-2021, DOI: 10.37532/2752-8081.21.5.22

Citation: Solai Rani P. Application of Graph Theory In Air-Transportation Network. J Pur Appl Math. 2021; 5(1):1:4.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

Graph theory is used for finding communities in networks. Graphs are used as device for modeling and description of real world network systems such are: transport, water, electricity, internet, work operations schemes in the process of production, construction, etc. Although the content of these schemes differ among themselves, but they have also common features and reflect certain items that are in the relation between each other. So in the scheme of transport network might be considered manufacturing centers, and roads and rail links connected directly to those centers.

In this paper is designed the solution for an practical problem to find a Minimum Spanning Tree by using Kruskal algorithm and graph search Dijkstra’s Algorithm to find the shortest path between two points, Also, for this case was developed a network model of the transportation problem which is analyzed in detail to minimize shipment costs and to find the eccentricity along with Jordon’s centre.

Keywords

Spanning tree, Minimum spanning tree, Shortest distance, Eccenticity

AMS Subject Classification: 05C69.

Introduction

Let G (V, E) be a graph, where V is a non-empty finite set. Whose elements are called point or vertices and E is a set of unordered pair of distinct elements of V (G). Every graph can be represented by a diagram where the vertices of the graph correspond to dots or small circle. Each edge corresponds to a line joining the vertices associated to it. Let G(V; E) be a graph, if the point of L(G) are the lines of G and two points in L(G) are adjacent .Then the corresponding lines are adjacent in G [1-4].

Graph Theory is ultimately the study of relationships. Given a set of airports and connections, which can abstract anything from city layouts to computer data, graph theory provides a helpful tool to quantify and simplify the many moving parts of dynamic systems .Studying graphs through a frameworkprovides answers to many arrangement, networking, optimization, matching and operational problems [5-12].

Results

Graph Theory in Air Traffic Control Network

Air traffic control is an essential element of the communication structure which supports air transportation. Two basic for air traffic control (ATC) are safely and efficiency of air traffic movement. ATC organizes the air space to achieve the objective of a safe, expeditious and orderly flow of air traffic. The increasing range of aircraft technology means more attention to the allotment of air space.

The problem is future compounded by the fact that busy airports sustain excessive lending and departure rates and airports themselves are invariably situated within busy terminal areas and in close proximity to other airports. Future more, these airports are often sited near the junction of air routers serving other destinations.

The term air traffic control is defined as service provided for the purpose of

• Preventing collision between aircraft on the air.

• Assist in preventing collision between aircraft moving on the apron or the maneuvering area.

• Expedite and maintain an orderly flow of air traffic and

Air route traffic control centers (ARTCC)

The ARTCC is to control air traffic network within the assigned area. That is the area which is outside the confines of air spaces designated for the provision of air traffic services by approach control and aerodrome control. Each centre has control of a definite geographic area and is concerned primarily with the control of aircraft operating under IFR. For ease of operation of work on area control unit is divided into sectors. These sectors are usually longitudinal in dimension having specific boundary which are delineated by en route reporting points. In some cases sectors are also divided vertically .Permitting a separate sector responsibility for the air routes within the upper air space. The sectors are required to work in close liaison, one with another, their manning and method of operation of being primarily determined by the nature of technical equipment provided to carry out the tasks. Aircraft must not be permitted to penetrate the airspace of another sector or ARTCC unless prior coordination has taken place. It can be observed that an aircraft flight plan is transferred between sectors within an ARTCC and between ARTCC’s when crossing the ARTCC boundary. At the boundary points marking the limits of ARTCC, the aircraft is released to and adjacent centre or to terminal control or an approach control facility

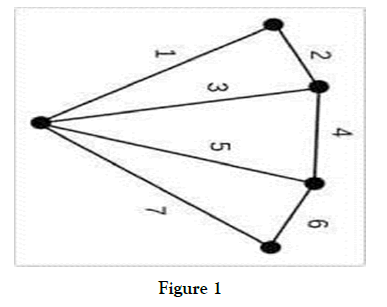
Terminal Approach Control: These purpose is to protect the flight path of aircraft leaving the airways system to land at the airport in the terminal or alternatively the flight path of aircraft departing the terminal for and en route airway. When these are several airports in and urban area .One facility may control traffic to all these airports. An approach control of busy airport can handle as many as fine stacks of arriving aircraft which have been transferred to it by ARTCC (Figure 1).

Figure 1

Air Traffic Control Tower

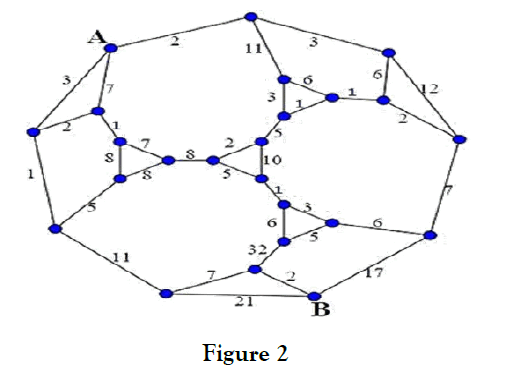
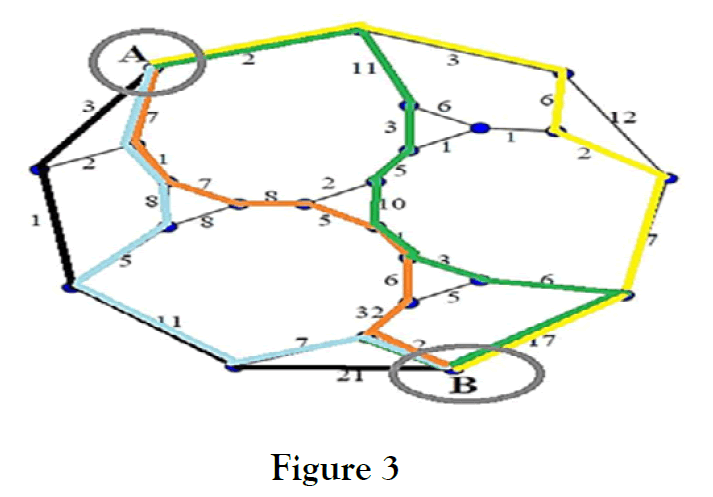
The modern airport, control room sits on the top of a concrete stalk or on top of a brick building placed at permissible height within the clearance angles of the airport runways. Seeing by eye, what is actually happening within the immediate environment of the airport and on its surface is what this part of the ATC service is all about. Usually at busy airports these would be two controller’s .The air controllers and the ground controller. Air controller is responsible for aircraft which are flying in the vicinity of airport traffic zone and for aircraft taking off and landing .Ground movement on the airport surface. It is essential for him to see, as much as possible of the airport surface including its taxi ways and exit point form the runway in use (Figure 2 & Figure 3).

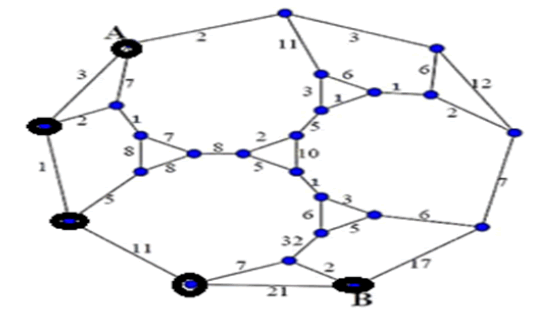
Graph theory provides many useful applications in Operations Research. A graph is defined as a finite number of points (known as airports or vertices) connected by lines (known as edges or arcs). In this paper for a given graph find a minimum cost to find the shortest path between two airports.

Figure 2

There are different path options to reach from airport A to airport B, but our aim is to find the shortest path with a minimum transportation costs, this requires a lot efforts.

Figure 3

Minimum spanning tree by using Kruskal’s Algorithm

In this paper the minimum spanning tree for the given case is described by several figures given in the following. We begin by placing all the airports of the given graph without arches, then we will start to put arches in their place starting from the lowest cost (arc length 1) to one with higher costs, but having in mind not to create cycles (step 1). This process continues by placing the second arc of length 2 (step 2)

Arch of lower cost that comes after him with units 1 and 2 is the arc of length 3. Again we have processed in the same way having in mind that we should not create cycles (step 3).

Applying this rule to all arches of the given Graph given, we have gained a minimum Spanning tree which is given in step 5. Arches which are removed from the graph because this happened since their deployment creates a cycles (step 5).

Minimum cost path

From the Minimum Spanning Tree shown in step 4, we are able to find the minimum cost path (trajectory) from airport A to airport B.As we can see in step 6 that there are two alternative ways to reach from airport A to airport B, which are distinguished by dash line.

Let’s start with first option to calculate the distance from airport A to airport B (dash line), the result is as follows: (here 1 unit =1000 km)= 2+3+6+7+4+5+2+5+4+3+6+17 = 64 units (this is the most expensive path)

For the second option (full line):

= 3+1+11+7+2 = 24 units

This means that the second option represents the minimum cost path from airport A to airport B.

Dijkstra’s Algorithm

By using Dijkstra’s Algorithm we are able to find the shortest distances (length of arc) from an airport to all other airports. Firstly, we start from the airport A, which is chosen as permanent airport. Analyzing the distances of the neighborhood airports from the airport A, we are able to find the shortest path to airport 2 (its distance is equal with 2). Afterwards airport 2 is chosen as permanent airport, and we have to check after the distances from airport 2 to the neighbor airports. To the each neighbor airport is added the length of the permanent airport.

Now is chosen the minimum distance from airport A. Minimum distance is chosen as permanent airport, since the 3+2 distance is shorter than 7, this means that distance 7 is not going to be considered anymore and we have to use the distance 5.

Now is chosen the minimum distance from airport A. For this case the permanent airport is chosen the minimum distance 4, this means that to all neighbour airport is added the distance of permanent airport. This process is repeated for each airport respectively.

For example, for the permanent airport 6 by adding distances 6+8=14 (in step 8) , is shown that 14>9, this means that the previous distance 9 remains, while the distance 14 is not considered anymore. This means that airport 9 is chosen as permanent airport and the procedure is similar to the previous cases.

Minimum path between airports A and B

Let’s find the shortest path from airport A to airport B, this is done starting from the airport B, by subtracting from this airport the distance between each airport.

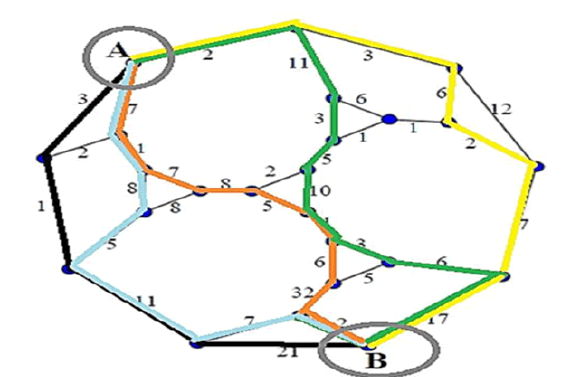
Eccenticity

The eccentricity ∈(v) of a graph vertex v in a connected graph G is the maximum graph distance between v and any other vertex u of G

Selecting from different route (Path) we have

Green

2+11+3+5+10+1+3+6+17=58

Yellow

2+3+6+2+7+17=37

Orange

7+1+7+8+5+1+6+32+2=69

Blue

7+1+8+5+11+7+2=41

Here the orange route has the maximum distance which gives the eccentricity

Algorithm

The Jordan center of a graph is the set of all vertices of minimum eccentricity that is, the set of all vertices u where the greatest distance d(u,v) to other vertices v is minimal. Equivalently, it is the set of vertices with eccentricity equal to the graph’s radius. Thus vertices in the center (central points) minimize the maximal distance from other points in the graph.

CONCLUSION

Dijkstra’s Algorithm will find the shortest path between two airports. Kruskal’s algorithm will find the minimum spanning tree connecting all the given vertices.

Basically, Dijkstra’s will find a connection between two vertices, while Kruskal’s will find a connection between ‘n’ number of vertices.

The results which are obtained for the example shows that Dijkstra’s Algorithm is very effective tool to find the path with lowest cost from airport A to airport B. Same results have been obtained also for Minimum Spanning Tree by using Kruskal’s algorithm, but this case the procedure is much simpler with a minimum spanning tree to reach airport B from airport A with the lowest total cost. I have tried also to find the worst scenario to reach airport B from airport A which is approximately 63% more expensive from the first case and is passenger-friendly route.

Whilst taking the longest path is expensive but will be both airline-passenger friendly as there are more number of airports as well as passenger will increase as to demanded airport, both flight planner and passengers wish to minimize the fare also taking the longest route with less number of airports compromises safety as any airline in case of emergency cannot make sudden maneuver to safety, this is where the Jordon’s central points can be of use for all the other airports in the structures for safety purposes.

REFERENCES

1. Arumugam S, Ramachandran S. Invitation to graph theory. New Gamma Publishing House. 1997.
2. Douglas I, West B. Introduction to graph theory. 2015.
3. Kumar Bisen S. Application of graph theory in transportation networks. Int J Sci Res. 2017; 5:6197-201.
4. Harary Graph theory by V. Krishna murti.( Pearsonprentice Hill 2015).
5. Pant, Neeraj & Faruqi, Shahab.2016. Graph theory.
6. Borasi A, Bisen SK. Operations research use in transportation problem. Int J Sci Res. 2017; 5:6226-6228.
7. Gupta C, Belokar RM. Applications of total quality management in Indian airline industry. Int J Sci Res. 2014; 3:1077-1081.
8. Rani, Solai. Line set domatic number of graphs. ALS. 2007; 1:167-74.
9. J Life Sci (JLS), ISSN 0117-3375.
10. Rani, Solai & Poovazhaki, Mrs.2015. The strong split domination number of a graph.
11. Graph O. Int J Math. 2015; 70-75
12. George JC, Khodkar A, Wallis WD. Graphs. In Pancyclic and bipancyclic graphs. 2016.