Bianchi type cosmological models with heat flow in Lyra's geometry

Received: 11-Jan-2023, Manuscript No. puljpam-23-6043; Editor assigned: 14-Jan-2023, Pre QC No. puljpam-23-6043 (PQ); Accepted Date: Jan 27, 2023; Reviewed: 16-Jan-2023 QC No. puljpam-23-6043 (Q); Revised: 17-Jan-2023, Manuscript No. puljpam-23-6043 (R); Published: 30-Jan-2023, DOI: 10.37532/2752-8081.23.7(1).01-09

Citation: Rajamahanthi S, Bora S, Komu SPS, et al. Bianchi type cosmological models with heat flow in Lyra’s geometry. J Pure Appl Math. 2023; 7(1):37-44.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

Bianchi type-V cosmological model along with perfect fluid and heat conduction have been discussed in the presence of Lyra’s geometry. By using the law of variation for the mean Hubble parameter the solution contains heat conduction and gauge function for and , which is related to the average scale factor of metric factor of metric and gives decelerating parameter. We discussed heat transmission stages from initial time to the late time of the universe. The relation between density and pressure is discussed. We obtain a constant decelerating parameter. Physical interpretation and thermodynamic laws are discussed.

Keywords

Cosmological models; Perfect fluid; Heat flow; Thermodynamics; Lyra geometry

Introduction

Since Einstein field equations contains cosmological constant causes the universe is in static mode. To avoid static nature of the universe in these field equations with zero density, general relativity requies to modify the description of Riemannian geometry by explaining flat space. In 1918 Wely has gave us a wonderful generalized Riemannian geometry, it unify both electromagnetism and gravitation of the universe. Due to no inerrability of transfer of length these theories were not satisfied. In 1970 Follond again gave us modification and formulation in Riemannian geometry called as modified Wely’s manifold which verifies many basic ideas [1-2].

In 1951 Lyra came with new ideology in Riemannian geometry with a wonderful toll named as gauge function in the low structure manifold. It accepts inerrability and cosmological constant naturally occurred in the geometry. Later many authors studied in different ways like Sen and Dunn introduced a new scalar-tensor theory and developed a clarification of the Einstein’s field equations with the help of Lyra’s geometry. Halford predicts theory with observational results which are same, as classical solar system tests are considered and he introduced the constant displacement vector ϕ_i in Lyra’s geometry [3-6]. It plays a vital role in the realistic treatment. Later Soleng came with the constant displacement field in Lyra’s geometry [7]. It will either include a creation field and be equal to Hoyle’s creation field in cosmology by Authors or contain a special vacuum field, it together with gauge vector and a cosmological term [8-10].

Several authors like were studied interacting scalar fields for different space-times in Lyra geometry [11-27].

In 1989 Bianchi developed Bianchi type cosmological models which are homogeneous and anisotropic. Bianchi models are less symmetric as compared with FRW models. The study of Bianchi type V models has considerable role in relativistic cosmology [28].

The author has an exact solution of the vacuum Brans-Dicke field equations for a spatially homogeneous and anisotropic metric. Author got FRW models in f(R) gravity and Authors have studied the solutions of Bianchi type–I and V space-times in the framework of f(R) gravity [29-33]. Authors proposed Bianchi type– III models with dark energy, Author has studied Bianchi type-I and type-II models, Authors has studied results of Bianchi type–V models, which were describing early stages of evolution of the universe [34-42]. The study of Bianchi type–V cosmological models creats more enthusiasm as these models contain isotropic special cases and permit arbitrarily small anisotropic levels at certain stages. These properties make the models suitable as models of our universe.

At present, the cosmological models are developed in general relativity under the supposition of the matter content of the universe. It can be described in a perfect fluid, While the supposition may be a better approximation to the original content of the universe, which effects such as heat conduction and magnetic fields may be considerable at earlier epochs of the evolution of the universe. As the matter is not attempting thermal equilibrium in the early stage of evolution of universe, it is evident to that the heat flow during transition stages. The effect of heat flow in the structure formation of the universe has been studied by several authors like has studied the cosmological models with heat conduction and explained the properties in the early stage of evaluation of universe [43-51].

From the motivation of above researchers, we studied Bianchi type – V cosmological model along with perfect fluid and heat flow in the frame work of Lyra’s geometry. The paper contains the following contents. In Section 1: Introduction. In Section 2: The Basic Equations and Quadrature Solution. In Section 3: Solution of filed equations. In section 4: The Thermodynamical Relation. In Section 5: Conclusions.

The Metric and Basic Equations

We Consider Bianchi Type–V model given by

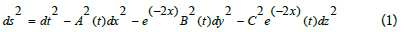
Here the functions A(t), B(t) and C(t) are functions of t and anisotropic directions of expansion in the normal 3-D space.

We define the following parameters to be used to solving Einstein’s field equations for the metric (1)

The Hubble’s parameter H is

Here the directional Hubble’s parameters , 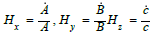are the in the direction of x, y and z respectively.

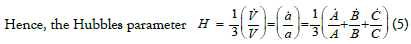
Now, we can see the most important scalar i.e., scalar expansion (θ), the shear scalar (σ2), and the mean anisotropy parameter (A_m) defined as follows :

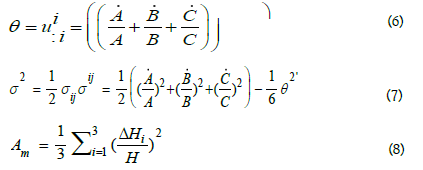
Where ΔH = H_i - H

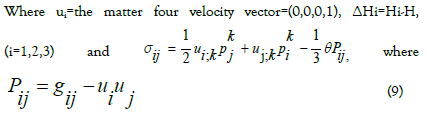
The field equations and their solutions

For Lyra’s geometry the field equation in normal gauge, by [4-5]

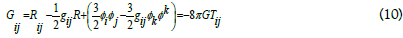
Here ϕ_i = the displacement vector = (0,0,0,β(t)) , and T_ij is the energy momentum tensor of the matter.

The energy momentum tensor for fluid with heat flow in presence perfect fluid matter is considered by

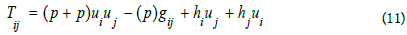
Where ρ energy density, p pressure, u_i fluid velocity, h_i is the heat flow vector, g_ij is the metric tensor and which satisfies

Now, we consider that the heat flow is in the x-direction such that h₁ = (h₁,0,0,0), where h₁ is function of time t.

Using Eqs. (1), (11), and (12), the field equations are

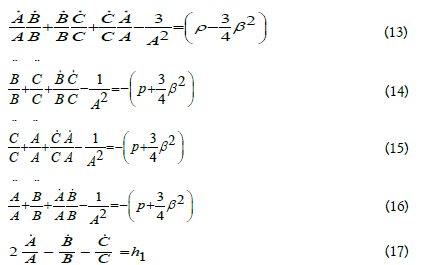
The energy conservation equation 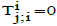gives

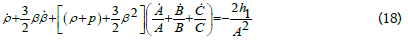
Equations (13)-(16) gives the following relation in terms of H,ρ,p,β is

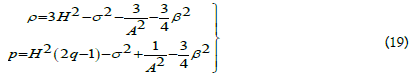
Solution of Field Equations

In the evaluation of universe the matter density Ω decelerating parameter q >0 did an extraordinary role. The universe decelerating when q >0 and accelerating when q<0 . By counting magnitude relation for galaxies to determining decelerating parameter q is so complicated due to evaluating effect. By the author Schuecker et.al. q0 is observed in the range -1.27 < q₀ < 2 , from the redshift survey in the study of galaxies count the value of q0 is observed as 0.1 withe upper limit q0 <0.75 . By the authors Riess et al , Permulater at al  they concluded that at present the universe is in accelerated expansion because they observed the range of decelerating parameter is -1≤q≤0 . It was identified that through the present observations of SNe I_a and CMB favour the accelerating model (q<0) .

Our aim is to solve the field equations (13)-(17) in the frame work Lyra geometry with creation matter and heat flow of the fluid. Since equation (1) are completely eigenized by average Hubble’s parameter H. Let us consider the parameter H is related to average scale factor a(t) .

By law of variation

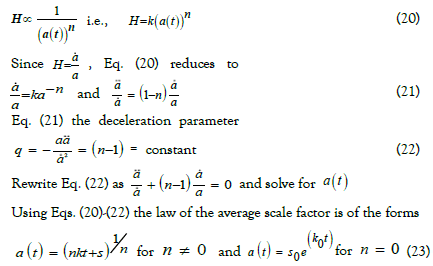
Where k, s, s₀, k₀ are constants of integration.

Depending on the value of “n”, here the model is two types, if k=0 in eq. (20) the model represents static universe and hence we need not pay any attention on it. When k>0 in eq. (20) consistently with observation for which the universe is expanding mode. The sign of decelerating parameter q represents the model is inflates of not. If q>0 (when (n-1)>0) relates to standard decelerating model whereas q<0 i.e., -1≤q≤0 (when -1<(n-1)<0) relates to inflation . The present day universe is Einstein-de Sitter universe with constant deceleration q=0.5 . Hence, we thought that the universe is in accelerated expansion form now.

Subtracting Eq. (14) from Eq. (15)

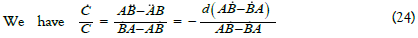
by Integrating this equation

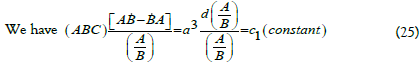
Again Integrating Eq. (25)

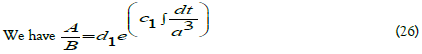
Similarly subtract eq. (14) from eq. (16) and eq. (15) from eq. (16) respectively we have

Where c₁ , c₂ , c₃ , d₁ , d₂ , and d₃ are integration constants and In explicit form for the metric functions are

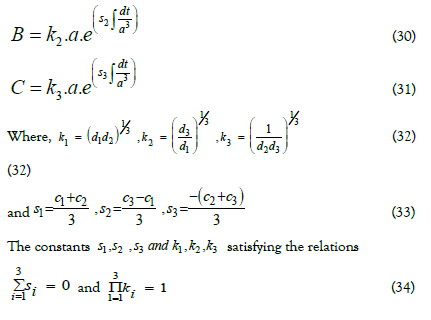
Case (i) when n=0

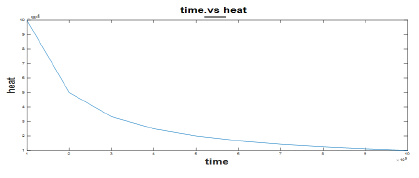
Since the universe under gone into a transition from early decelerating expansion phase to the current accelerating expansion phase, so the cosmological models represents transit cosmological model Figure 1.

Figure 1: Clearly the heat conduction is a decreasing function of t and it heat is large at early universe stage of universe and cools down in the accelerating universe.

From Eq. (23)

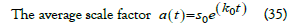
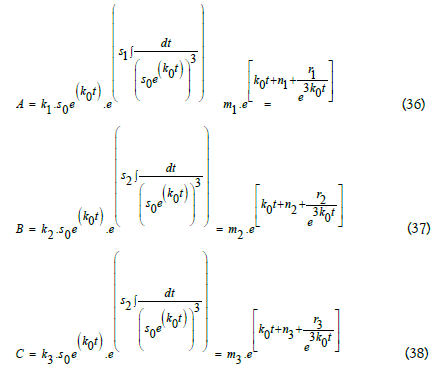
Where are constant and l_i = int.for i = 1, 2, 3 respectively

By Eq. (35)-(38)

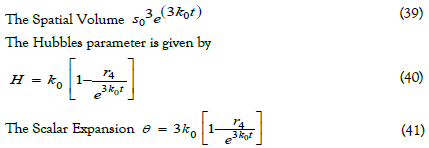
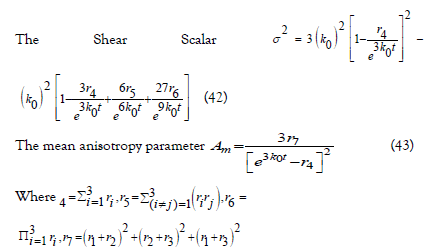
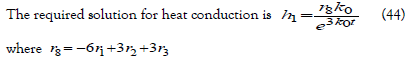
By Eq. (22) for n=0

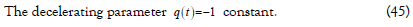
Clearly q<0 i.e., -1≤q<0 (when n=0), the cosmological model represents to the universe is inflation in this case.

Since the fluid is formed from particles, it satisfies an equation of state of the form

Using Eq. (19) and Eq.(40) the perfect pressure and density is given by

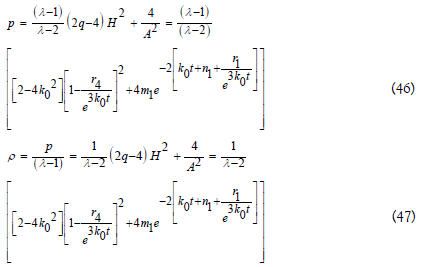
λ - 2 ≠ 0, for λ - 2 ≠ 0 Using Eqs. (19), (41), (42), (46), and (47) the expression for gauge function is obtained by

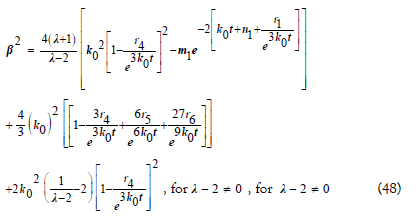
Physical interpretation of the model for (n=0)

By above observations here are three physical interpretations are required to discuss for 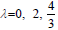of the equation of state given by the equation.

False vaccum model

If λ =0 in this model then the equation of state p=(-1)ρ , it represents the ‘false or degenerate vaccum’ and the explicit form of pressure and density are obtained in this model are

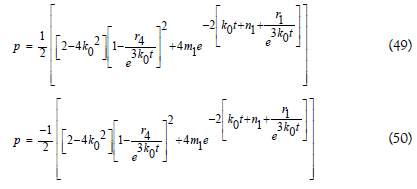
Radiating model

If 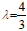in this model then the equation of state is 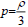, it represents the matter distribution with radiation not ordered and a universe in which most of the energy density in the form of radiation and hence the model is called ‘Radiating model’. Here the explicit form of pressure and density are obtained in this model are

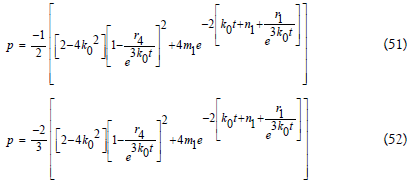
Zel’dovich fluid Model

Since 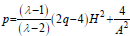does not obtained when λ =2 , so there is no discussion about this case.

By the above results , at early stage of universe (t = 0) the metric functions A(t), B(t), C(t) and spatial volume V(t), the physical parameters σ, θ, A_m, σ², p, ρ and heat low(h₁) all becomes constant at initial epoch, so it indicates that the universe starts with the constant parameters physically and geometrically. By observing at late time universe i.e., t→∞ , A(t), B(t), C(t) tends to infinity and p+ρ =0 causes the universe is accelerating because of negative pressure. The men anisotropic parameter and shear scalar vanish. The heat flow becomes negligible means that the universe is cooling down. The spatial volume and scale factor exponentially expanded for late time.

Case (ii) when n≠0

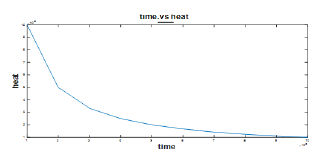
Since the universe undergone into a transition from early decelerating expansion phase to the current accelerating expansion phase, so the cosmological models represents transit cosmological model Figure 2.

Figure 2: Clearly the heat conduction is a decreasing function of t and it heat is large at early universe stage of universe and cools down in the accelerating universe.

From Eq. (23)

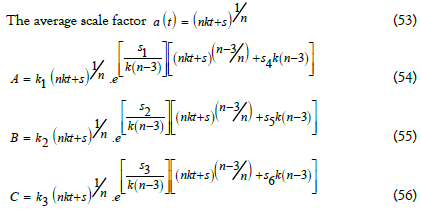
By Eq. (35)-(38)

The spatial volume

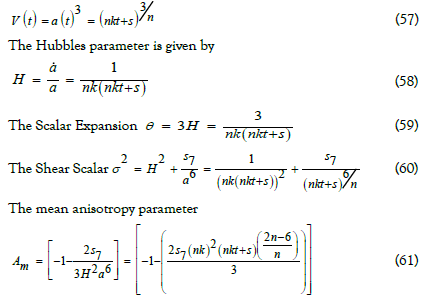
Where,

k₁ , k₂ , k₃ and s₁ , s₂ , s₃ , s₇ = s₁ , s₂ , s₃ are constant and s₄ , s₅ , s₆ are int.constants,

By Eq. (22) The decelerating parameter

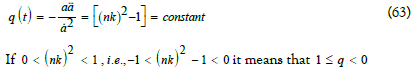
If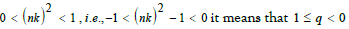

Clearly, q<0 , so that the cosmological model represents to the universe is inflation in this case .Since the fluid is formed from particles, it satisfies an equation of state of the form p=( λ-1)ρ , for 0≤ λ≤2 and Using Eq. (19) and Eq. (58) the perfect pressure and density is given by,

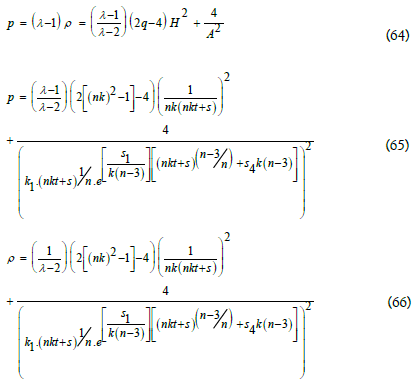
Using Eq. (19), (32), (33) and (56) the expression for gauge function is obtained by

Physical interpretation of the model for (n=0)

By above observations here are three physical interpretations are required to discuss for 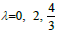of the equation of state given by the equation.

False vaccum model

If λ=0 in this model then the equation of state is p=(-1)ρ, it represents the ‘false or degenerate vaccum’ and the explicit form of pressure and density are obtained in this model are

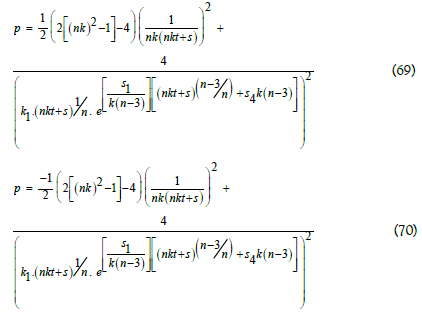
Radiating model

If 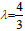in this model then the equation of state is 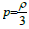, it represents the matter distribution with radiation not ordered and a universe in which most of the energy density in the form of radiation and hence the model is called ‘Radiating model’. Here the explicit form of pressure and density are obtained in this model are

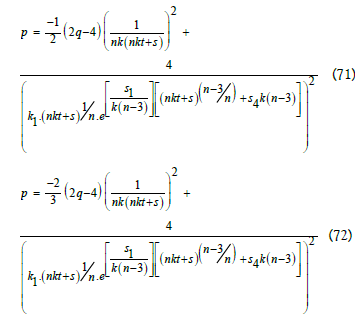
Zel’dovich fluid Model

If λ=2 in this model then p=ρ , But pressure and density are not obtained for this case so there is no discussion about this case.

By the above results, at early stage of universe (t = 0) the metric functions A(t), B(t), C(t), and spatial volume V(t), physical parameters σ, θ, A_m, σ², p, ρ and heat low(h₁) tends to infinity. By observing at late time i.e., t→∞ , the metric functions are A(t),B(t),C(t) intermediate and p , ρ becomes zero .The physical parameters σ, θ, A_m, σ² also tends to zero as t→∞ It represents that the universe is expanding with cosmic time and the rate of expansion is decreasing ,hence the model becomes isotropic for late time.

The Thermodynamical Relation

Baryon conservation law

Let 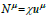be the particle flux and x is the particle density We know that the standard cosmology, conservation of total particle number is

Where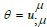is the expansion of the fluid

Integrate this equation and use Eqs. (39),(43) (56) and (60) which gives particle number density as

In case of n = 0 , at t=0 the particle density is constant, it indicates that heat conduction is constant or disappear and hence it is uniform in the early stage of evolution universe.

In case of n ≠ 0 , at t = 0 the particle density has play more influence during early stage of evolution of universe.

Temperature gradient law

The heat conduction expression if given by

Where k ≥ 0 is the coefficient of heat conduction (thermal conductivity), T is the temperature of the universe and u_v = 0 zero acceleration flow vector. Since the heat flux is retained as x-component, we have

For case n = 0 the x-component of temperature gradient is

For n ≠ 0 case the x-component of temperature gradient is

On simplifications of Eq. (73) and (74) we get temperature distributions as

For n ≠ 0 case the temperature distribution is

Where ε₁ and ε₂ are integration constants, these are arbitrary functions of t or constants. At early stage of universe (t = 0) the temperature distribution T is diverges and hence k becomes finite. As time t tends to infinity T tends to ε₁ and ε₂ in both the cases of n respectively. Hence the universe is at equilibrium stage at late time state of universe.

Conclusion

In this paper, we studied Bianchi type-V cosmological model along with perfect fluid and heat conduction in presence of Lyra’s geometry. By using the law of variation for the mean Hubble parameter the solution contains heat conduction and gauge function for n = 0 and n ≠0, which is related to the average scale factor of metric and gives decelerating parameter. For , we observed at early stage of universe (t = 0) the metric functions A(t), B(t), C(t) and spatial volume V(t), the physical parameter σ, θ, A_m, σ², p, ρ and heat low(h₁) all becomes constant , so it indicates that the universe starts with constant parameters physically and geometrically. By observing at late time universe i.e., t → ∞ , A(t), B(t), C(t) tends to infinity. The men anisotropic parameter and shear scalar vanish. The heat flow becomes negligible means that the universe is cooling down. The spatial volume and scale factor exponentially expanded for late time. By the case n = 0 , we observed at early stage of universe (t = 0) the metric functions A(t), B(t), C(t), and spatial volume V(t), physical parameters σ, θ, A_m, σ², p, ρ and heat low(h₁) tends to infinity. By observing at late time i.e., t → ∞ , the metric functions are A(t), B(t), C(t) intermediate , p, ρ becomes zero and the physical parameters σ, θ, A_m, σ² also tends to zero. It represents that the universe is expanding with cosmic time and the rate of expansion is decreasing, hence the model becomes isotropic for late time. We discussed transition states of heat flow from evaluation time to the late time of the universe. We obtain gauge function in both cases and discussed different stages of the universe using the relation between p and ρ . We obtained a constant decelerating parameter. Physical interpretation of thermodynamic laws was discussed.

Declarations

We hereby declare that,

Ethical Approval

1. The content of the manuscript has not been published anywhere and it is the output of authors’ genuine and honest research.

2. This paper has not been sent to any journal for consideration.

3. This paper completely exhibits the analysis and findings of the authors’ own and honest work.

Competing interests

All the authors/contributors declare that they have no competing interests" in this section.

Authors' contributions

The author R Santhikumar drafted the entire paper including calculations and final structure, the B Satyanarayana author given graphs and analysis, the authors Suryanarayana P S Kornu and P E Satyanarayana contributed in the calculations of the results and helped in the collection of required literature.

Funding

Not Applicable

Availability of data and materials

No data is used to this article for generating or analyzing the results during the current study only the simplified form of mathematical calculations were included in the above resultant equations.

References

1. Narlikar JV, Hoyle F. New theory of gravitation. Proc R Soc London Ser A 282 1(1964).

   [Google Scholar] [Crossref]

2. Hoyle F, Narlikar JV. On the nature of mass. Nature. 1971 Sep 3;233(5314):41-4.

   [Google Scholar] [Crossref]

3. Bhamra KS. A cosmological model of class one in Lyra's manifold. Aus J Phy. 1974;27(4):541-8.

   [Google Scholar] [Crossref]        

4. Karade TM, Borikar SM. Thermodynamic equilibrium of a gravitating sphere in Lyra's geometry. Gen Relativ Gravit. 1978;9:431-6.

   [Google Scholar] [Crossref]

5. Kalyanshetti SB, Waghmode BB. A static cosmological model in Einstein-Cartan theory. Gen Relativ Gravit. 1982;14(10):823-30.

   [Google Scholar] [Crossref]   

6. Reddy DR, Innaiah P. A plane symmetric cosmological model in Lyra manifold. Astrophys space sci. 1986;123:49-52.

   [Google Scholar] [Crossref]

7. Reddy DR, Venkateswarlu R. A static conformally flat cosmological model in Lyra's manifold. Astrophys space sci. 1987;136:183-6.

   [Google Scholar] [Crossref]

8. Singh T, Singh GP. Bianchi type‐I cosmological models in Lyra’s geometry. J Math Phys. 1991;32(9):2456-8. 

   [Google Scholar] [Crossref]

9. Singh T, Singh GP. Bianchi type III and Kantowski-Sachs cosmological models in Lyra geometry. Astrophys space sci. 1991;181:89-101.

   [Google Scholar] [Crossref]

10. Singh GP, Desikan K. A new class of cosmological models in Lyra geometry. Pramana. 1997;49:205-12.

    [Google Scholar] [Crossref]

11. Pradhan A, Pandey HR. Bulk Viscous cosmological models in Lyra geometry. arXiv preprint. 2003;9.

    [Google Scholar] [Crossref]

12. Pradhan A, Vishwakarma AK. A new class of LRS Bianchi type-I cosmological models in Lyra geometry. J Geom Phys. 2004;49(3-4):332-42.

    [Google Scholar] [Crossref]

13. Mohanty G, Mahanta K L  and Sahoo R R Non-Existence of Five Dimensional Perfect Fluid Cosmological Model in Lyra Manifold. Astrophys Space Sci. 2006;4(1):8-10

    [Google Scholar] [Crossref]

14. Casana R, Melo CA, Pimentel BM. Electromagnetic field in Lyra manifold: a first order approach. Braz J phys. 2005;35:1151-4.

    [Google Scholar] [Crossref]

15. Bali R, Chandnani NK. Bianchi type-III bulk viscous dust filled universe in Lyra geometry. Astrophys Space Sci. 2008;318:225-30.

    [Google Scholar] [Crossref]

16. Kumar S, Singh CP. An exact Bianchi type-I cosmological model in Lyra's manifold. Int J Mod Phys. 2008;23(6):813-22.

    [Google Scholar] [Crossref]

17. Singh JK, Sharma NK. Anisotropic dark energy Bianchi Type-II cosmological models in Lyra geometry. Int J Theor Phys. 2014;53:1375-86.

    [Google Scholar] [Crossref]

18. Desikan K, Das S. A New Class of Cosmological Models in Lyra Geometry in the Presence of Particle Creation. Int J Pure Appl Phys. 2017;13(4):303-9.

    [Google Scholar] [Crossref]

19. Bianchi V. Übersicht der palaearktischen Arten der Gattung Carpodacus Kaup. J Ornithol. 1898;46:102-23.

    [Google Scholar] [Crossref]

20. Adhav KS, Katore SD, Rane RS, et al. Zero mass scalar field with bulk viscous cosmological solutions in Lyra geometry. Astrophys Space Sci. 2009;323:87-90.

    [Google Scholar] [Crossref]

21. Brans C, Dicke RH. Mach's principle and a relativistic theory of gravitation. Phy rev. 1961;124(3):925.

    [Google Scholar] [Crossref]

22. Paul BC, Debnath PS, Ghose S. Accelerating universe in modified theories of gravity. Phy Rev D. 2009;79(8):83534.

    [Google Scholar] [Crossref]

23. Sharif M, Shamir MF. Exact solutions of Bianchi-type I and V spacetimes in the f (R) theory of gravity. Class Quantum Gravity. 2009;26(23):235020.

    [Google Scholar] [Crossref]

24. Sharif M, Shamir MF. Plane symmetric solutions in f (R) gravity. Mod Phys Lett. 2010;25(15):1281-8.

    [Google Scholar] [Crossref]

25. Reddy DR, Santikumar R, Naidu RL. Bianchi type-III cosmological model in f (R, T) theory of gravity. Astrophys Space Sci. 2012;342:249-52.

    [Google Scholar] [Crossref]

26. Reddy DR, Santhikumar R, Pradeep Kumar TV. Bianchi type-III dark energy model in f (R, T) gravity. Int J Theor Phys. 2013;52:239-45.

    [Google Scholar] [Crossref]

27. Santhikumar R. Anisotropic Bianchi Type-I Dark Energy Model in Alternative Theory of Gravitation. The Int J Aanaly  Exp  modal analy. 2019; 3275-3279  

    [Google Scholar] [Crossref]

28. Santhikumar R. General Bianchi Type Dark Energy Cosmological model in Modified theories of Gravitation. Int J Aanaly  Exp  modal analy. 2019; 3280-3283  

    [Google Scholar] [Crossref]

29. Pradhan A, Kumarsingh A, Chouhan DS. Accelerating Bianchi type-V cosmology with perfect fluid and heat flow in Saez-Ballester theory. Int J Theor Phys. 2013;52(1):266-78.

    [Google Scholar] [Crossref]

30. Ahmed N, Pradhan A. Bianchi type-V cosmology in f (R, T) gravity with Λ (T). Int J Theor Phys. 2014;53(1):289-306.

    [Google Scholar] [Crossref]

31. Sharma UK, Zia R, Pradhan A. Transit cosmological models with perfect fluid and heat flow in Sáez-Ballester theory of gravitation. J Astrophys Astron. 2019;40(1):1-9.

    [Google Scholar] [Crossref]

32. Singh CP. LRS Bianchi type-V cosmology with heat flow in scalar: tensor theory. Braz J Phys. 2009;39:619-28.

    [Google Scholar] [Crossref]

33. Ram S, Zeyauddin M, Singh CP. Anisotropic Bianchi type V perfect fluid cosmological models in Lyra’s geometry. Braz J Phys. 2010;60(11):1671-80.

    [Google Scholar] [Crossref]

34. Roy SR, Prasad A. Some LRS Bianchi type V cosmological models of local embedding class one. Gen Relativ Gravit. 1994;26(1):939-50.

    [Google Scholar] [Crossref]

35. Van Leeuwen WA, Kox AJ, De Groot SR. On relativistic kinetic gas theory: XIV. Transport coefficients of a binary mixture. General expressions. Phys A: Stat Mech Appl. 1975 15;79(2):233-55.

    [Google Scholar      ] [Crossref]

36. Novello M, Reboucas MJ. The stability of a rotating universe. Astrophys J. 1978 ;225:719-24.

    [Google Scholar] [Crossref]

37. Coley AA, Tupper BO. An exact viscous fluid FRW cosmology. Phys Lett . 1983;95(7):357-60.

    [Google Scholar] [Crossref]

38. Coley AA, Tupper BO. Imperfect fluid cosmologies with thermodynamics-some exact solutions. Astrophys J. 1984;280:26-33.

    [Google Scholar] [Crossref]

39. Sviestins E. Some rotating, time-dependent Bianchi type-IX cosmologies with heat flow. Gen relativ gravit. 1985;17:521-3.

    [Google Scholar] [Crossref]

40. Mukherjee G. Shear-free homogeneous cosmological model with heat flux. J Astrophys Astron. 1986;7:259-73.

    [Google Scholar] [Crossref]

41. Banerjee A, Sanyal AK. Irrotational Bianchi V viscous fluid cosmology with heat flux. Gen relativ gravit. 1988;20:103-13.

    [Google Scholar] [Crossref]

42. Deng Y. Solutions of the Einstein equation with heat flow. Gen relativ gravit. 1989;21:503-7.

    [Google Scholar] [Crossref]

43. Coley AA. Bianchi V imperfect fluid cosmology. Gen relativ gravit. 1990;22:3-18.

    [Google Scholar] [Crossref]

44. Coley AA, Hoogen RV. Qualitative analysis of diagonal Bianchi type V imperfect fluid cosmological models. J Math Phys. 1994;35(8):4117-44.

    [Google Scholar] [Crossref]

45. Chan R. A Shearing Non-Adiabatic Solution of Einstein's Equations. Astrophys space sci. 1997;257:299-309.

    [Google Scholar] [Crossref]

46.  Roy SR, Banerjee SK. Bianchi VI0 electric type cosmological models in general relativity with stiff fluid and heat conduction. Gen Relativ Gravit. 1996;28:27-33.

    [Google Scholar] [Crossref]

47. Singh JK. Some cosmological models with heat and null radiation flow. Astrophys Space Sci. 2007;310:241-4.

    [Google Scholar] [Crossref]

48. Schuecker P, Ott HA, Seitter WC, et al. The Muenster Redshift Project. III. Observational constraints on the deceleration parameter. Astrophys J. 1998;496(2):635.

    [Google Scholar] [Crossref]

49.  Riess AG, Filippenko AV, Challis P, et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998;116(3):1009.

    [Google Scholar] [Crossref]

50. Perlmutter S, Aldering G, Valle MD, et al. Discovery of a supernova explosion at half the age of the Universe. Nature. 1998;391:51-4.

    [Google Scholar] [Crossref]

51.  Perlmutter S, Aldering G, Goldhaber G, et al. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys J. 1999;517(2):565.

    [Google Scholar] [Crossref]