+447723598358
Classical wave equation: A gross error in mathematics and physics
Received: 04-May-2024, Manuscript No. puljpam-24-7098; Editor assigned: 06-May-2024, Pre QC No. puljpam-24-7098(PQ); Accepted Date: May 27, 2024; Reviewed: 10-May-2024 QC No. puljpam-24-7098(Q); Revised: 15-May-2024, Manuscript No. puljpam-24-7098(R); Published: 31-Jul-2024, DOI: 10.37532/2752- 8081.24.8(4).01-06
Citation: Kalanov TZ. Classical wave equation: A gross error in mathematics and physics. J Pure Appl Math. 2024; 8(4):01-06.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
A detailed proof of the incorrectness of the classical wave equation is proposed. The correct methodological basis for the proof is the unity of formal logic and rational dialectics. The proof leads to the following irrefutable statement: The classical wave equation and the derivation of the classical wave equation are a gross error in mathematics and physics. The proof of this statement is based on the following irrefutable main results:
1.The first gross error is the following approximaterelationship: “sine of angle is approximately equal totangent of angle; cosine of angle is approximatelyequal to 1”. This relationship means (implies) that thequantity of the angle and the right-angled triangle donot exist. Consequently, the relationship between thetangent of the angle and the derivative of thedisplacement with respect to coordinate does notexist;
2.The second gross error is that the second-orderderivative of the displacement with respect tocoordinate does not exist, because the dimensions ofdisplacement and coordinate are “meter”, the first-order derivative of the displacement with respect tocoordinate is dimensionless quantity (i.e. the first-order derivative of the displacement respect tocoordinate has no the dimension “meter”);
3.The third gross error is that the first-order derivativeof the displacement with respect to coordinate cannot
be expanded into the Taylor series, because the second-order derivative of the displacement with respect to coordinate does not exist;
4.The fourth gross error is as follows:
a)The left side of the wave equation containsthe condition that time is a variable quantity,and the coordinate is a constant quantity;
b)The right side of the wave equation containsthe condition that time is a constant, and thecoordinate is a variable. This means (implies)that the equation contains contradictoryconditions (propositions). Therefore, theequation represents a violation of the formal-logical law of the lack (absence) ofcontradiction;
5.The fifth gross error is that the standard derivation ofthe equation relies on the following false theories:negative number theory, complex numbers theory,trigonometry, vector calculus, differential calculus, andNewton's second law.
Key Words
Mathematical physics; Foundations of theoretical physics; Foundations of mathematics; Wave equation; Formalisms in classical mechanics; Newtonian mechanics; Mechanical and elastic waves; String variations; History of science; Philosophy of science; Formal logic; Higher education
Introduction
The derivation of the classical wave equation (i.e., the equation ofstring vibrations) and the solution of the equation is a significantachievement of mathematical physics and mechanics of the 18th century [1-5]. In 1727 Johann Bernoulli derived a difference equation related to the vibrating string problem. In 1746 the work of Johann Bernoulli was extended by Jean d’Alembert who derived the wave equation and obtained its solution. Jean d’Alembert, Leonhard Euler, Daniel Bernoulli, Luigi Lagrange and Joseph Fourier made significant contributions to finding a solution to the equation and further development of the theory of vibrations. But the debate on correct solution of the wave equation between d’Alembert, Euler and Bernoulli showed that the problem of correct solution of the equation has not been completely and finally solved. Why?
Currently, the derivation of the classical differential equation for string vibrations is presented in physics and mathematics courses. The derivation and solution of this classical wave equation is based on negative number theory, complex number theory, metric geometry, trigonometry, vector calculus, differential calculus, the theory of forces, and Newton’s second law. In my conviction, differential calculus as a theory of infinitesimal quantities cannot contain mathematical operations on numbers because differentials of variables (i.e., infinitesimal quantities) do not take numerical values. The geometric interpretation of the derivative is a gross error. Vector and force are physical concepts (but not mathematical concepts) because vector and force do not have the dimension “meter” and cannot exist in a geometric coordinate system. Standard trigonometry contains many errors and is therefore not a science. Newton’s second law is a blunder. From this point of view, there is a need for a modern critical analysis of the standard derivation of the classical wave equation.
The purpose of this work is to propose a detailed and irrefutable proof of the falsity of the classical wave equation. The correct methodological basis for the proof is the unity of formal logic and rational dialectics. The unity of formal logic and rational dialectics is the correct criterion of truth.
Standard derivation of the classical wave equation
Standard statement of the problem: As is known, a string is a thin material thread that can be bent under forces. If a stretched string is in a state of equilibrium without the action of external forces, then its position coincides with the ruler OX in the Cartesian (metric) coordinate system XOY. If the string is disturbed from its equilibrium position by an external force, then the string will vibrate. In the case of transverse vibrations, all points of the string are moved in the perpendicular direction relative to the ruler OX. The quantity of displacement of the points of the vibrating string relative to the ruler OX is the desired quantity.
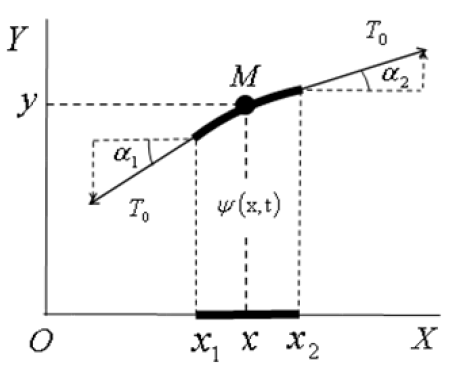
The mathematical description of the displacement is determination of the positions of an elementary string segment at different points of time t. The displaced elementary string segment is under the actionof two tension forces T0 which are directed along tangent lines to the ends of the string segment and form angles α1 and α2 with the ruler OX (Fig 1).
Figure 1: Transverse vibrations of the continuous string in the Cartesian (metric) coordinate system XOY. The element (segment) of the string in the equilibrium state is on the ruler OX. The string tension forces T0 are applied to the points 1 and 2 of the string element which is in the non-equilibrium state. The material point M of the string segment is a mobile point and has coordinatesxand yat certain point of time t. The coordinatesxand yare variable quantities.
The string tension forces T0 are applied to different end points of the string element and are therefore connected (non-free) vectors. The displacement ψ(x, t) characterizes the position of the movable point M of the string segment (the string is the geometric locus of the position of the point M). The statement of the problem is as follows: one must derive a linear differential equation for the displacement ψ(x, t) as a function of the coordinate x and time t.
Standard solution of the problem: The first step is to add up (sum up) the forces (vectors) acting on the element (segment) of the string. In accordance with vector calculus, the analytical rule for addition of vectors is to add up (sum up) the projections of the vectors onto coordinate rulers. This rule leads to the following analytical expression for the sum of the projections of the forces onto the ruler OY:
FY(t) = T0sinα2 - T0sinα1
where the member (term) FY(t) is the Y-projection of the total force acting on the segment; the member (term) -T0sinα1 is the Y-projection of the force applied to the point 1 of the segment; the member (term) T0sinα2is the Y-projection of the force applied to the point 2 of the segment; time t is a parameter. The dimensions ofthe quantities are as follows:
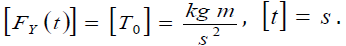
The second step is to express the quantity FY(t) in terms of the quantities ψ(x, t) and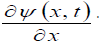 
The quantities ψ(x, t) and 
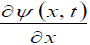have the following dimensions:
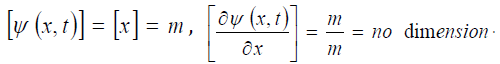
In the case of small string vibrations, one makes the following approximations:
sinα1 = tgα1, sinα2 = tgα2, cosα1 = 1, cosα2 = 1.cosα = 1
where α (α1 ≤ α ≤ α2) is the variable quantity of the angle formed by the ruler OX and the tangent line at the point M. Quantities sinα and tgα have no dimensions: [sinα] = [tgα] = no dimension. In this case, theequation (condition) of the balance of the forces has the following form:
FY(t) = T0sinα2 - T0sinα1 = 0
In addition, one makes the following approximations:
(where t is a parameter).
The third step is to express the quantity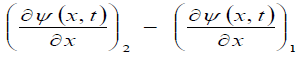 
in terms of the quantity 
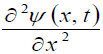( where t is a parameter). According to theorems of pure mathematics, if the function 
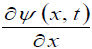can be expanded into an infinite series in degrees of the quantity (x - x1), then this functional series is the Taylor series for this function in a neighborhood of the point x1. In this case, the function 
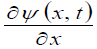must be continuous and differentiable an infinite number of times in the interval of convergence of the series. If
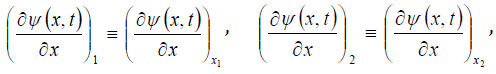
then the Taylor series for the function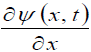 
is
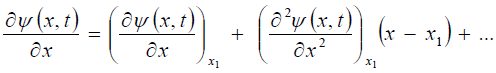
If the value x = x2 belongs to the neighborhood of the point x1, then substitution of the value x = x2 into the Taylor formulaleads to the following relationships:
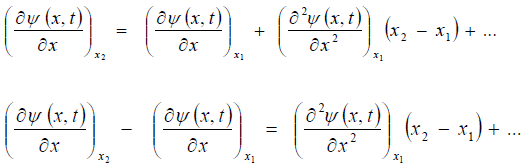
where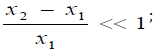 
t is a parameter.
One postulates that
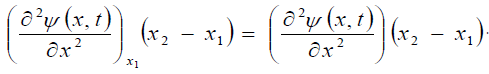
In this case, the equation (i.e. condition) of the balance of the forces has the following form:
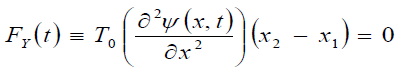
where t is a parameter.
The fourth step is to obtain the equation of motion of the string based on d’Alembert’s principle. According to d’Alembert’s principle, one must add a force of inertia to the left side of the relationship
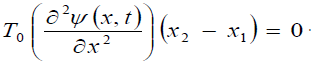
According to Newton’s law, the force of inertia of the element (segment) of the string is equal to the product of the mass of the element and the acceleration of the element:
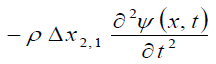
where ρ is the linear density of the string; Δx2,1; x2 - x1;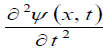 
is the acceleration; t is a variable.
In this case, the equation of motion (i.e., the condition for the balance of all forces) has the following form:
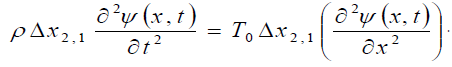
Thus, the classical wave equation is the following:
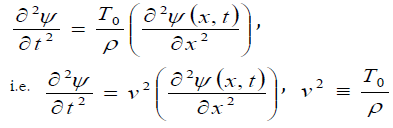
where the dimensions of the quantities are as follows:
The solution of this equation was proposed by d’Alembert.
Critical analysis of the classical wave equation
If it is supposed that negative number theory, complex number theory, trigonometry, vector calculus, differential calculus, and Newton’s second law are correct theories, then the errors in the derivation of the wave equation are as follows.
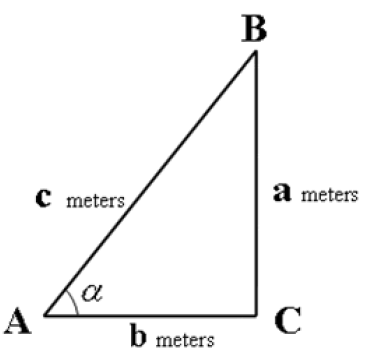
The first gross error is the following approximate relationships: sinα1 = tgα1, sinα2 = tgα2, cosα1 = 1, cosα2 = 1.cosα = 1, sinα = tgα. Really, as is known, the standard relationships for the right-angled triangle ΔABC in figure 2:
Figure 2: Right-angled triangle ΔABC. The triangle exists if a ≠ 0 , b ≠ 0, c ≠ 0, a ≠ c, b ≠ c
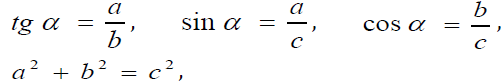
or, in detailed notations,
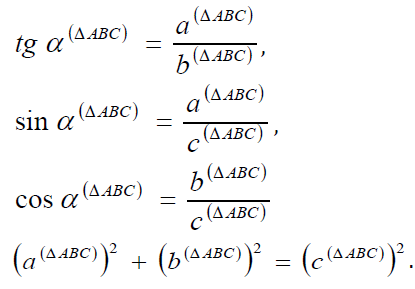
If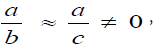 
then b≈c. In accordance with the Pythagorean theorem, the relationship b≈c means that a≈0. In this case, the following contradiction arises: 0 ≠a =0 (From the point of view of formal logic, the signs “ ≠ and =" are identical). Therefore, the right-angled triangle ΔABC and the angle α do not exist under tgα ≈ sinα , cosα ≈ 1. The relationships 
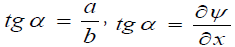are nonsense.
The second gross error is the quantity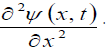 
Really, the quantity 
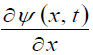has no dimension:
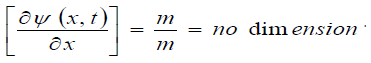
Therefore, the second-order derivative with respect to x is nonsense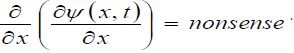 
Taylor series forthe function 
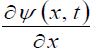does not exist.
The third gross error is the following postulate:
Really, the quantity x1 is a constant, and the quantity x is avariable. This postulate represents the formal logical error - the violation of the law of lack of contradiction:
(constant quantity) ≠ (variable quantity)
Thus, the classical wave equation is fabrication, utter nonsense.
Discussion
Thus, the classical wave equation is a gross error.
Really, if one takes into account (consideration) the proven fact that the theory of negative numbers, the theory of complex numbers, trigonometry, vector calculus, differential calculus and Newton's second law are erroneous theories, then one will comprehend that the derivation of the wave equation is a gross error. As a result, this gross error leads to false differential equation for free vibrations of the string:
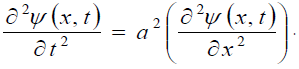
Really, the formal-logical error in this equation is the existence of the following contradiction: the left side of this equation contains the condition (statement) " t = var; x = const", and the right side contains the contradictory condition (statement) " t = const; x = var". From the point of view of formallogic, a mathematical relationship containing contradictory statements (propositions) is incorrect. In other words, the formal logical error is a violation of the law of lack (absence) of contradiction:
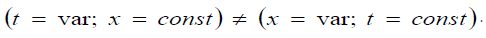
The derivation of the classical wave equation is based on the concept “displacement of a physical quantity from an equilibrium value.” The concept “physical quantity” means (signifies, implies) that the quantity of displacement has the dimension of a physical quantity. The displacement is described by the function ψ(x, t) where thevariable quantity x is the Cartesian (metric) coordinate of thedisplaced material point, and the variable quantity t is time. Thecoordinates of the material point are measured with metric rulers OX and OY in the Cartesian coordinate system XOY. Therefore, the coordinates of the material point are neutral numbers with the dimension “meter”. If any object has no the dimension "meter", then this object does not exist in the Cartesian (metric) coordinate system XOY. (In other words, this object has no geometric meaning). For example, information quantity t and properties of material objects (for example, geometric quantities of angle and area, physical quantities of length, speed, acceleration, force and vector) have no a geometric meaning and, therefore, do not exist in the system XOY.
Any line segment in the metric system XOY is described by a single mathematical expression y = f(x) where y is function ofargument x; quantities y and x have the dimension “meter”.But the properties of a line segment (for example, the length of a line segment) or the properties of a geometric figure (for example, the quantity of an angle, the quantity of an area, etc.) do not exist in the system XOY. In other words, the properties of geometric (material) objects cannot be depicted (displayed, expressed, represented) in the system XOY, because the properties of material objects do not represent material objects. The properties of material objects are the result of measurements and calculations.
The process of rationalization of thinking has not affected scientists, because scientists do not rely on the correct methodological basis (i.e. scientists do not work within the framework of the correct methodological basis): the unity of formal logic and rational dialectics. The unity of formal logic and rational dialectics is the only correct criterion of truth that scientific theories must satisfy. Therefore, all old theories must be questioned. The names of the classics of science should not serve as a cloak (cover, screen) for false theories.
The achievements of theoretical physics and mathematics seem convincing, but they turn out to be unfounded. Therefore, the foundations of theoretical physics and mathematics enter into the crisis. This implies greatest sign of our time.
Conclusion
Thus, the classical wave equation is a gross error in physics and mathematics. The irrefutable proof of this statement is based on the correct methodological analysis of the standard derivation of the classical wave equation. The correct methodological basis for analysis is the unity of formal logic and rational dialectics. The analysis leads to the following main results:
1. The first gross error is the following approximaterelationship: “sine of angle is approximately equal totangent of angle; cosine of angle is approximatelyequal to 1”. This relationship means (implies) that thequantity of the angle and the right-angled triangle donot exist. Consequently, the relationship between thetangent of the angle and the derivative of thedisplacement with respect to coordinate does notexist.
2. The second gross error is that the second-orderderivative of the displacement with respect tocoordinate does not exist, because the dimensions ofdisplacement and coordinate are “meter”, the first-order derivative of the displacement with respect tocoordinate is dimensionless quantity (i.e. the first-order derivative of the displacement respect tocoordinate has no the dimension “meter”).
3. The third gross error is that the first-order derivativeof the displacement with respect to coordinate cannotbe expanded into the Taylor series, because thesecond-order derivative of the displacement withrespect to coordinate does not exist.
4. The fourth gross error is as follows:
a)The left side of the wave equation containsthe condition that time is a variable quantity, and the coordinate is a constant quantity;
b)The right side of the wave equationcontains the condition that time is aconstant, and the coordinate is a variable.This means (implies) that the equationcontains contradictory conditions(propositions). Therefore, the equationrepresents a violation of the formal-logicallaw of the lack (absence) of contradiction.
5. The fifth gross error is that the standard derivation ofthe equation relies on the following false theories:negative number theory, complex numbers theory,trigonometry, vector calculus, differential calculus,and Newton's second law.
Thus, the classical wave equation does not satisfy the criterion of truth and is not a scientific achievement.
References
- Courant R, Hilbert D. Methods of mathematical physics. Phys Today. 1954;7(5):17.
- Whitham GB. Linear and nonlinear waves. John Wiley & Sons. 2011.
- Wheeler GF, Crummett WP. The vibrating string controversy. Amer J Phy. 1987;55(1):33-7.
- Graff KF. Wave motion in elastic solids. Courier Corporation. 2012.
- Kalanov TZ. Logical analysis of the foundations of differential and integral calculus. Bull Pure & Appli Sci Math Statis. 2011;30(2):325-32.
