+447723598358
Collatz conjecture is true: A definite conclusion is drawn by using the principle of net induction rate and net reduction rate
Received: 02-Jan-2024, Manuscript No. puljpam-24-6981; Editor assigned: 03-Jan-2024, Pre QC No. puljpam-24-6981 (PQ); Accepted Date: Mar 12, 2024; Reviewed: 15-Jan-2024 QC No. puljpam-24-6981 (Q); Revised: 31-Jan-2024, Manuscript No. puljpam-24-6981 (R); Published: 31-Mar-2024, DOI: 10.37532/2752- 8081.24.8(2).01-02
Citation: Chattopadhyay C. Collatz conjecture is true: A definite conclusion is drawn by using the principle of net induction rate and net reduction rate. J Pure Appl Math. 2024; 8(2): 01-02.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
This research work establishes a theory for concluding an armative answer to the famous, long-standing unresolved problem “The Collatz Conjecture".
Key Words
Reduction rate; Collatz problem; Sequential values; Experimental evidence; Probabilistic
Introduction
In the well-known Collatz problem i.e., 3n + 1 problem is the following:
If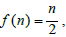 
when n is even and
.......... = 3n + 1, when n is odd,
do the sequential values of f(n) eventually reach to 1, for every natural number n ?
This problem was pursued by many researchers along dierent directions.
Following are, among others, some of the important methods available in the literature:
1.Experimental evidence,
2.A probabilistic heuristic argument,
3.Use of encoding matrix,
4.Generalization of the problem.
Obviously, experimental evidences cannot provide a satisfactory solution to the problem.
In probabilistic heuristic approach the following idea is explained:
If we choose n at random in the sense that it is odd with probability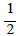 
and even with probability 
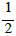then the Collatz function f1: N→N increases n by a factor roughly 
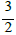half the time and decreases it by a factor of 
the time.
Furthermore, if n is uniformly distributed modulo 4, one easily verifies that f1 is uniformly distributed modulo 2 and so 
should be roughly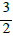 
as large as f1(n) half the time and roughly 
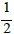times as large as f1(n) the other half of the time. Continuing this at a heuristic level, we expect generally that
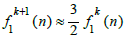half the time, and
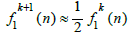the other half of the time.
The logarithm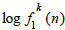 
of this orbit can be modelled heuristically by a random walk with steps 
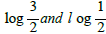occuring with equal probability. The expectation 
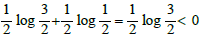and so (by the classic gambler's ruin) we expect the orbit to decrease over the long term. This can be viewed as the heuristic justification of the Collatz Conjecture.
But this probabilistic approach cannot ensure a clear solution to the problem.
The generalized form of the problem is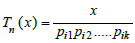 
where pi's are primes less or equal to pn dividing the numerator and 
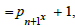if no prime 
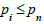divides x.
Using this generalized form, the author used the concept of encoding matrix and generalized some results in the paper of Terras. But the author upheld a heuristic argument against the existence of divergent conjectures, which also cannot give a satisfactory answer to the main problem.
In 1985 J.C. Lagarias pursued the problem by using Weakly connected graph of the Collatz Graph. Lagarias had the following comment in his article `The 3x + 1 problem and its generalizations':
“Of course there remains the possibility that someone will find some hidden regularity in the 3n+1 problem that allows some of the conjectures about it to be settled.
The existing general methods in number theory do not seem to touch the 3n+1 problem. In this sense it seems intractable at present.
Study of this problem has uncovered a number of interesting phenomena. It also serves as a benchmark to measure the progress of general mathematical theories. For example, future developments in solving exponential diphantine equations may lead to the resolution of the definite cycles conjecture."
A new approach is established in this research work which concludes an affirmative answer to the problem. This approach invents the ‘Principle of Net Induction Rate and Net Reduction Rate'.
Five main sections are there in this article to achieve the required goal. Second section contains preliminaries and some basic results.
Third section introduces concepts of Immediate odd predecessors and Immediate odd successor and studies some vital observations.
Fourth section deals with the study of dependence of C-convergence of naturals of the form 4n+3 on C-convergence of the naturals of the form 3ω − 1 and 3μ - 2.
Fifth section introduces the concepts of Collatz Decisive Subset, Net Induction Rate, Net Reduction Rate and finally draws a definite conclusion to the problem.
Preliminaries
For any natural number n, if the Collatz sequence of n eventually reaches to 1, we write the fact as n→1. For example,7→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1. This will be written simply as 7→11→17→13→5→1, ignoring the even terms. This will be called Collatz sequence of 7, as we have started with 7 itself. Since 7 eventually reaches to 1, we write 7→1 and say that 7 C-converges to 1'.
Observation 1.
(i) Any odd natural number x(> 4) can be one of the following forms:
x = 4n + 1 for some n ∈ N,
x = 4n + 3 for some n ∈ N.
(ii) for any n ∈ N we have the following observation on Collatz sequences:
4n + 1→12n + 4→6n + 2→3n + 1.
This will be written in short as 4n + 1→3n + 1.
(iii) let n be odd. Then
4n + 1→1iff n→1.
This follows immediately because 4131nn+→+and since n is odd, we have n→3n + 1.
By a reduction of an odd natural x, we shall mean that in the Collatzs equence of x, x eventually reaches to some y, where y<x.
For example, 9→28→14→7. So 9 has a reduction.
Note that every even 2t has a reduction and for any 4t+1, since 4t+1→3t+1,4t+ 1 has a reduction.
The following result holds:
Theorem 1
The following statements are equivalent:
i. n→1 for all n ∈ N
ii. 4n + 3 has a reduction for each n ∈ N.
