Comparative Study of the Life Time of Black Holes due to Non-relativistic & Relativistic effect
Received: 04-Jan-2023, Manuscript No. puljmap-23-6067; Editor assigned: 05-Jan-2023, Pre QC No. puljmap-23-6067(PQ); Accepted Date: Jan 21, 2023; Reviewed: 06-Jan-2023 QC No. puljmap-23-6067(Q); Revised: 13-Jan-2023, Manuscript No. puljmap-23-6067(R); Published: 30-Jan-2023, DOI: 10.37532/puljmap.2023 .6(1); 01-03.
Citation: Mahto D. Comparative Study of the Life Time of Black Holes due to Non-Relativistic & Relativistic effect. J Mod Appl Phys. 2023; 6(1):1-3
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
The present research paper discusses the comparative study of the life time of black holes due to Non-relativistic and Relativistic effect using the model Γ = 2.098(M/M⊕)3×1067 years as proposed by Stephen Hawking and the model for variation of mass with velocity which concludes that the life time of the black holes due to relativistic effect is greater than to the life time of the black holes due to non-relativistic effect and also twice to the life time of black holes of mass equal to the sun due to non-relativistic effect having velocity equal to the velocity of light.
Key Words
Life time, relativistic life time and Spinning velocity
Introduction
The death of a star of a mass greater than 5 solar masses due to a supernova explosion gives birth to black holes and hence it has a definite life time [1]. Everything like materials, messages and information etc. are absorbed by the black holes, while the quantum mechanical treatment of black holes gives the concept for the emission of particles from black holes in the form of Hawking radiation [2]. The concept for effective black body radiation from a black hole has been introduced by Hawking in terms its temperature and the Stefan Boltzmann constant [3,4]. The statistical analysis of lif etime and temperature of the black holes existing in X-ray binaries and Active Galactic Nuclei have been studied. The life time of black holes is transformed in terms of Chandrasekhar limit(Mch) and their values of some black holes have been calculated [5]. In the present research paper, we have discussed the comparative study of the life time of black holes due to Non relativistic and Relativistic effect using the model
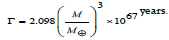
Theoretical Discussion
In terms of solar mass the life time (in year) of a black hole of mass M is given by the following equation [6]:

The spinning velocity of some of black holes have ranging from 50% to 99% of the velocity of light and hence the mass of black holes will vary with velocity as per special theory of relativity as [7,8]:

M0 is the rest mass and v is the spinning velocity of black holes.
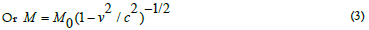
Using equation (3) into equation (1) and solving with proper mathematical operations finally, we obtain the equation and designated it by Γrel
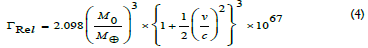
Now, we solve the following terms using binomial theorem and neglecting the higher power of terms
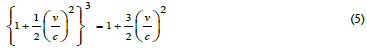
Putting the above value in the equation (4), we have
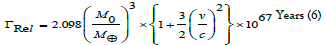
The equation (6) is known as relativistic life time of spinning black holes with spinning velocity v.
The ratio for the life time of the black holes due to non-relativistic and relativistic effect can be obtained by dividing eqn (1) by the equation (6) as:
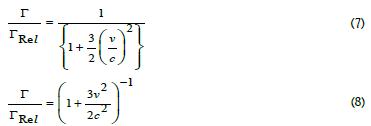
Using the binomial theorem to expand the above equation and neglecting the higher powers of terms
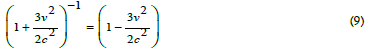
Now from equation (8), we have

Let us consider the above equation for the study of ratio of life time and relativistic life time of spinning black holes having spinning velocity 50% to 100% of the velocity of light.
For the spinning black holes having the velocity 50% of the velocity of light (v/c=1/2), the equation (16) becomes

Similarly for the spinning black holes having the velocity from 60% to 100% of the velocity of light, the equation (10) is solved and tabulated in the table 1, we have
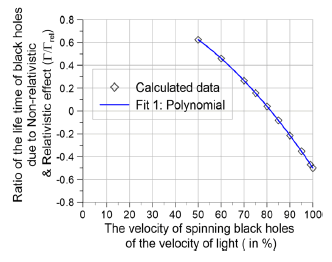
TABLE 1 Comparative Study of the Lifetime of black holes due to Nonrelativistic & Relativistic effect
| S. No. | The velocity of spinning black holes of the velocity of light (in %) | Ratio of the velocity of spinning black holes and the velocity of light(v/c) | Ratio of the life time of black holes due to Non-relativistic & Relativistic effect |
|---|---|---|---|
| 1 | 50 | 0.5 | 0.625 |
| 2 | 60 | 0.6 | 0.46 |
| 3 | 70 | 0.7 | 0.765 |
| 4 | 75 | 0.75 | 0.156 |
| 5 | 80 | 0.8 | 0.04 |
| 6 | 85 | 0.85 | -0.083 |
| 7 | 90 | 0.9 | -0.215 |
| 8 | 95 | 0.95 | -0.353 |
| 9 | 99 | 0.99 | -0.47 |
| 10 | 100 | 1 | -0.5 |
For the black holes having maximum rate of spinning velocity (v=c), equation (6) becomes as follows:
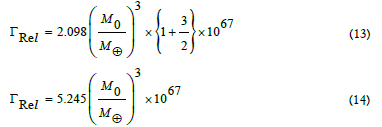
Dividing (1) by (14), we have

For the black holes having mass equal to the mass of our sun, the above equation becomes

It is obvious from eqn (1) and (16) that it will be impossible to calculate the life time of the black holes, because, a black hole with the mass of the Sun would take 2×1067 years to evaporate and takes 5.245×1067 years to evaporate the black holes due to relativistic treatment. Both times are enough long, whereas the age of universe is only 13.8×109 years.

Result
In the present model, we have applied the variation of mass with velocity to get the relativistic effect of the life time of spinning black holes. It is clear from the equation (1), the life time of the black hole about some multiple of 1067 years, which is enough long period. After applying the relativistic effect on the life time of the spinning black holes, we obtain the equation (6) for the relativistic life time of the black hole which is greater than the life time of the black holes due to non-relativistic effect. The life time for both cases is so long that the universe's age is very small compared with the life of the black holes. In a particular case of black hole having mass equal to the sun, the life time is too long.
Discussion
The above fact can be clearly explained with proper data as: It is obvious from eqn (1) that it will be impossible to calculate the life time of the black holes, because, a black hole with the mass of the Sun would take 2×1067 years to evaporate whereas the age of the universe is only 13.8×109 years and hence it will take more than 1057 times the current age of the universe for that black hole to evaporate. The relativistic life time of the black holes with the mass of the Sun would also take 5.245×1067 years to evaporate the black holes, whereas the age of the universe is only 13.8×109 years and hence it will take more than 1057 times the current age of the universe for that black hole to evaporate. From the observation of figure 1 of the percentage of spinning velocity of black holes of speed of light along x-axis and the ratio of life time of spinning black holes due to the nonrelativistic & relativistic effect along y-axis, it is seen that the variation is followed by the polynomial equation of degree two represented by
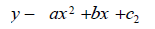
where, a=0.01496181145, b=0.0006421241055, c2=0.314162157 and polynomial nature of degree 2 of graph for this model gives fitting accuracy equal to 0.999999 showing the best fitting for the data and of 99.99% accuracy of proposed model. The relativistic effect holds good for the velocity, when it is comparable with velocity of light.
Conclusion
The relativistic effect holds good for the velocity, when it is comparable with velocity of light. From the fact given above, it is concluded that the relativistic life time of spinning black holes decreases slightly with increase of speed of spinning black holes compared to that of the non-relativistic life time. The life time of the black holes due to relativistic effect is greater than to the life time of the black holes due to Non-relativistic effect and also twice to the life time due to Non-relativistic effect having velocity equal to the velocity of light and mass equal to the sun.
ACKNOWLEDGEMENT
This work is devoted in memory of great scientist Stephen Hawking (March 14, 2018). The present work is a part of the research project proposal of BCST under Department of Science & Technology, Govt. of Bihar.
References
- Prakash V et al. Statistical analysis of life-time and temperature of black holes. Am. J. Theor. Appl. Stat.,2013;2(6):228-32.,
- Bowaire AN. Hawking Temperature of the Reissner-Nordstrom-Vaidya Black Hole. J. Math. Fundam. Sci., 20131; 45(2).
- Hawking SW. The quantum mechanics of black holes. Sci. Am., 1977 1; 236(1):34-42.
- Hawking SW. Particle creation by black holes. InEuclidean quantum gravity 1975:167-188.
- Jha BK et al. Study of Black Hole Radiation Power.
- Moore TA. A general relativity workbook. Mill Val.: Univ. Sci. Books; 2013.
- Reich ES. Spin rate of black holes pinned down. Nature. 2013; 500(7461):135.
- Nozieres P and Pines D. The Theory of Quantum Liquids: Superfluid Bose Liquids. CRC Press; 2018.