Constant C makes the ABC conjecture hold

Received: 08-Aug-2023, Manuscript No. puljpam-23-6671; Editor assigned: 09-Aug-2023, Pre QC No. puljpam-23-6671 (PQ); Accepted Date: Aug 28, 2023; Reviewed: 19-Aug-2023 QC No. puljpam-23-6671(Q); Revised: 20-Aug-2023, Manuscript No. puljpam-23-6671(R); Published: 30-Sep-2023, DOI: 10.37532/2752-8081.23.7(5).289-290

Citation: Xiaohui L. Constant C makes the ABC conjecture hold. J Pure Appl Math. 2023; 7(5):289-290.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

The ABC conjecture in number theory was first proposed by Joseph Oesterlé and David Masser in 1985. Mathematicians declare this conjecture using three related positive integers a, b, and c (satisfying a+b=c). The conjecture states that if there are certain prime powers in the factors of a and b, then c is usually not divisible by the prime powers.

This paper utilizes the fact that the prime factor among all factors in the root number rad (c) can only be a power of 1. Then, analyze all combinations of c that satisfy rad (c)=c, calculate the value of the combination, and find the maximum and minimum values of the root number rad, as well as the maximum exponent between them. Using this maximum index, an equivalent inequality is constructed to prove the ABC conjecture.

Keywords

Root; Prime factor; Conjecture; Constant C

Introduction

The positive integers a, b, and c, satisfying the following conditions: a+b=c , and (a, b)=1 ( a , b are mutually prime).

It is not difficult to find that when all factors in rad (c) are prime numbers and the powers of prime numbers are all 1, then rad(c) = c.

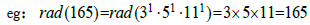
Through the prime number theorem, we know that given a positive integer x, the number of prime numbers that do not exceed xis approximately: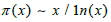

Now let's set the value range of the positive integer c to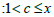

We set the number of prime numbers not exceeding x to be a positive integer h, so the value of h is: 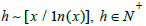,We use the set X = {p₁, p₂...p_n} to represent the set of all prime numbers that do not exceed the integer x[1].

Easy to detect: when 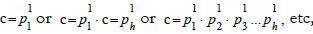The value of rad(c) is exactly equal to c , that is:

c = rad(c)

We can calculate the maximum number of combinations in the set of prime numbers where rad(c) = c is:

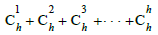
Because (a,b) =1, then (a,b, c) =1

Proof:

If a and c are not prime each other, there must be a common divisor k, and because b=c-a, then b and a must also have a common divisor k, which contradicts the prime of a and b, so a, b, and c are also prime each other

If the power of all prime factors in the radical rad(c) is 1, then c = rad(c), then: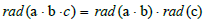

Now let's return to 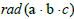for analysis：

We know that the minimum value of prime factors in rad(a^.b^.c) is 2, and the minimum number of these prime factors is 1. Therefore, the minimum value of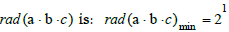

Similarly, when the power of the prime factor in 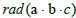is equal to 1 and its number is the integer 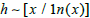, then the maximum value of 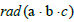is:

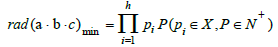
So we can immediately launch:

Now let's set 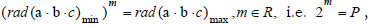to find the maximum exponent between the minimum and maximum values. by taking the logarithm of both sides of the equation, we can obtain the value of m as:

Let's analyze the value of c:

We know that the value range of c is: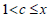

We know that the set X = {p₁, p₂...p_n} is a set of all prime numbers that does not exceed the integer x , so the construction of the value of the integer c must be: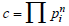

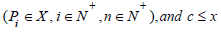
If x is an even number, then we can set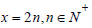

There must be an odd prime number 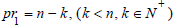and an odd prime number 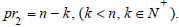The relationship between them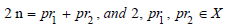

So the following two inequalities always hold:

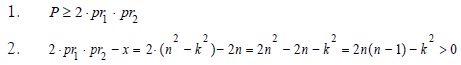
Similarly, immediately available: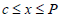

So whether x is odd or even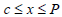

And because 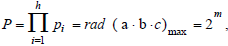we can immediately obtain:

Because 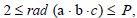then inequality (3) can be transformed as follows:

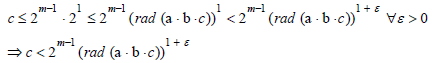
We set C = 2^m-1 and now we have found the constant that always holds the inequality above, namely:

C = 2^m-1.

Conclusion

In positive integers, there is equation a + b = c and (a,b) = 1, when ∀ε>0,∃C can make these triplets (ABC) satisfy the following inequality, namely:

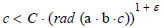
The following inequality holds:

Example:

a = 3, b = 5, and c = 8 , rad(a) = 3 , rad(b) = 5, rad(c) = 2,

rad(ab) = 15,rad(abc) = 30, so X = {7,5,3,2}

So,

rad(c)_min = 2, rad(c)_max = P = 7×5×3×2 = 210

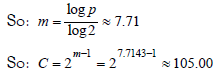
The following inequality holds:

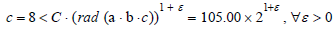
Conclusion: The ABC conjecture holds.

References

1. Green B, Tao T. The primes contain arbitrarily long arithmetic progressions. To appear. Ann. Math. 2005.

   [Google Scholar] [Crossref]

2. Xiaohui Li ,Proof of the Goldbach's Conjecture.2023-07-29 [Google Scholar] [Crossref]