Dark energy and dark matter
Received: 13-Mar-2023, Manuscript No. puljpam-23-6279 ; Editor assigned: 14-Mar-2023, Pre QC No. puljpam-23-6279 (PQ); Accepted Date: Mar 28, 2023; Reviewed: 17-Mar-2023 QC No. puljpam-23-6279(Q); Revised: 18-Mar-2023, Manuscript No. puljpam-23-6279 (R); Published: 31-Mar-2023, DOI: 10.37532/2752-8081.23.7(2).134-137
Citation: Jöge FM Dark energy and dark matter. J Pure Appl Math. 2023; 7(2):134-137.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
The rudiments of a theory of dark energy. The theoretical result is confronted with the numerical value calculated from the available data. Excellent matching of numerical values resulting in three independent paths makes the approach plausible. The work at hand is analogous to Kepler`s laws of planetary orbits. Only Isaac Newton put Kepler`s laws on a theoretical basis, which is provided here by Thomas Gornitz. The empirical Balmer formula for the frequencies of the spectral lines in the arc spectrum of hydrogen was also theoretically justified by Niels Bohr who calculated the energy levels of the hydrogen atom and the frequencces of spectral lines.
Keywords
Dark energy, Dark matter, Planck time, Age of the universe, Cosmic information
Introduction
The derivation of a formula for calculating dark energy is described. The result is tested on the basis of the available data from the max planck Institute for Radio Astronomy. Further formulas are deducted. The dark matter of the cosmos is calculated. A balance sheet is drawn up. Conclusions are drawn.
Derivation of a formula for calculating dark energy
Dark energy can be calculated if one makes the assumptions that Planck time tp is an oscillation period τ and dark energy satisfies the Planck/Einstein formula

Oscillations are fundamental oscillations of the cosmic space [1]. Thomas Görnitz says: “Structural quanta emerge from a quantum-theoretical description of “oscillation states” of a system around its ground state. They produce many effects. The AQIs of protyposis are also structural quanta and not particles. One can interpret them as the “fundamental oscillations of the cosmic space”
For dark energy Ed this then leads to:
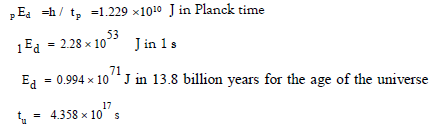
The following formula for calculating the dark energy in the universe is then derived from these calculation steps:

This simple three-sentence operation was founded by Thomas Gornitz in a more in-depth manner, resulting in very well-matched numerical values [1]. A connection to the empirical is thus achieved. Data shows us the nature of things as well as theories.
Verification of the result
In order to show the good concordance of the value calculated according to the formula of dark energy with the value calculated from the existing data, the data from the Max Planck Institute for Radio Astronomy are used as a basis. Accordingly, the mass/energy of the universe is composed as follows:
70% dark energy, 25 % dark matter ,4-5% visible baryonic matter and 0.3% neutrinos
In Grenzgebiete der Wissenschaft the energy equivalent for the visible matter in the universe is deducted as follows:
For the theoretical calculation, the universe is considered to be a single black hole, just as one imagines, according to a popular theory, the final stage of the universe [2]. Thomas Gornitz has also expressed the idea of the cosmos as a single black hole [1]. He writes: “From this point of view, it makes perfect sense to think about whether our cosmos can be interpreted under certain aspects as the interior of a gigantic black hole.”
Then, with the black hole entropy (Bekenstein-Hawking entropy) 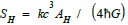 and Hawking temperature
and Hawking temperature 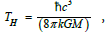 one obtains the formula
one obtains the formula 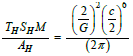 If one sets THSH = QH = E = Mc2 and for the area of the black hole event horizon AH = 4πR2 , which measures the information potentially contained in it, one obtains for the visible mass M of the universe
If one sets THSH = QH = E = Mc2 and for the area of the black hole event horizon AH = 4πR2 , which measures the information potentially contained in it, one obtains for the visible mass M of the universe 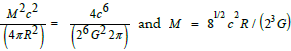
With the
HUBBLE relation
R = c / H0 yields  given by
given by

a numerical value that Stephen Hawking calculated for the entire current visible mass energy equivalent of the universe [3]. This theoretically calculated value, which corresponds to 1080 proton masses, and which makes up the major part of the cosmic energy of the matter, can be compared with the value calculated from the volume and density of the universe [4]. This value agrees well with the theoretically calculated value.
With H0= 2.285·10-18 s-1this results in the dark energy:
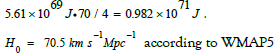
Whilst the matching of numeric values cannot replace a theory, a good theory must nevertheless be measured according to the concordance of numerical values. In this respect, the calculation supports the assumptions (theory) made for the formula (1.2).
A further possibility of validation is given through the application of the equation (4) from Grenzgebiete der Wissenschaft [2].
Accordingly, the energy is equivalent to the information flow H/t:

Hartmut Ising and Lienhard Pagel also developed a corresponding formula [5,6].
The formula (2.2) should be deducted exactly here from the De Broglie formula;
The De Broglie formula is A / h = S / k This results in
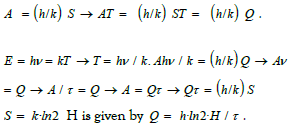
If one then sets Δt = aτ (a = dimensionless factor), then
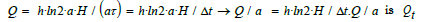
With Qt = Et one obtains the formula (2.2).
It is identical to ISING's or PAGEL's formula except for the factor ln2 [7].
Thus, dark energy can also be understood as information flow.
The cosmic information HK is given in Thomas Gornitz as approx. 10122 bit for tu = 15 billion years [8]. From this, formula (3.2) calculates the cosmic information HK = 0.943 × 10122 bit for tu = 13.8 billion years. HK = 0.943 × 10122 bit for the cosmic information and tu = 4.358 × 1017 s yields Ed = 0.994 × 1071 J for dark energy. So here too, very good concordance is evident.
Derived formulas
Using the equations (1.2) and (2.1) leads to the ratio of the energy equivalent of dark energy and visible matter
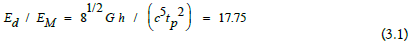
For the area of astrophysics, it might be relevant to theoretically calculate this relationship.
The following relationship for cosmic information HK can be derived from the formulas (1.2) and (2.2)

This formula (3.2) was also derived by Thomas Gornitz in a comparable form [1].
The maximum possible information content
Hmax which can
encode the surface of a spherical universe and which corresponds to
this surface in Planck units, is given by 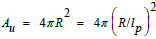 [9].
[9].
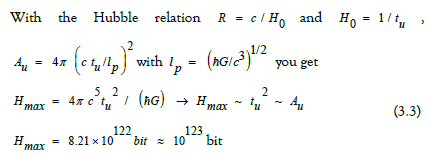
This value is in good agreement with the one identified by R. Penrose [10].
For comparison, the Bekenstein-Hawking entropy is cited:

Calculation of dark matter
According to Thomas Gornitz, the number of AQIs (abstract
quantum information) in the cosmos is 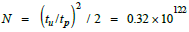 [1]This value corresponds to the
value of dark matter in Table 1, where
HDM = 0.33 × 10122 is given.
[1]This value corresponds to the
value of dark matter in Table 1, where
HDM = 0.33 × 10122 is given.
TABLE 1 Mass energy and information balance of the universe
| symbol | % | information 10122 [bit] | energy 1071 [J] | mass 1053 [kg] | [J/bit] | |
|---|---|---|---|---|---|---|
| dark energy | HK = HDE | 70 | 0.943 | 0.994 | ||
| dark matter | HDM = N | 25 | 0.337 | 0.355 | 3.9 | |
| visible baryonic matter | HM | 4,5 | 0.054 | 0.056 | 0.625 | Oct-51 |
| neutrinos | HNeu | 0.3 | 0.004 | 0.0043 | ||
| Σ | Hu | 100 | 1.338 | 1.4093 | ||
| HBH | 0.1634 (contained in Hu) | |||||
| Hmax | 8.21 | |||||
| MKG | 4.51 |
That`s a remarkable match!
With formula (3.2) it follows:

By comparing in Table 1, the information equivalents of the dark energy HDE = HK and the total mass energy of the universe Hu , one obtains the relation

and
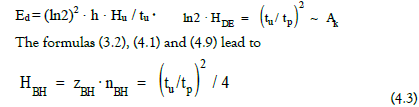
By combining the different information equivalents of the energies in Table 1, a number of formulas of the ratios of the information equivalents can be derived. Here are examples:
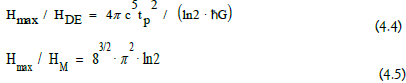
The formulas (3.2) and (4.3) lead to
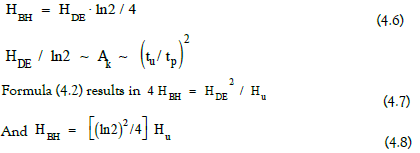
According to Thomas Gornitz, the information equivalent of the total black holes in the universe is

The number of AQIs that make up all black holes in the universe is therefore N / 2 = 0.3268 × 10122 / 2 = 0.1634 ×10122 . The entropy for black holes as objects in the cosmos is always smaller than the number of AQIs that form the black hole [11-14].
Preparation of the balance sheet
If you enter the values found in a table, you get the following picture:
Th. GOrnitz specifies MKG = 5.5 × 1053 kg for the “cosmic total mass”, which means a useful match [1].
Compilation of the formulas
There are three formulas in literature for the equivalence of information flow and energy. They are listed in Table 2, Figure 1.
TABLE 2 Compilation of the most important formulas
| Author | formula | determined | deducted further formulas |
|---|---|---|---|
| ISING H. and Pagel L. | IE = h H/tu | Hu | Ed = h tu/tp2 |
| JoGE F | JE = h · ln2 · H/tu | HDE | ln2 · HDE = (tu/tp)2 |
| Sedlacek KL. and Gornitz TH. | -D. GE = (ln2/12π2) h H/tu2 | HNeu | HDE = (2ln2) N |
| HDM2 = (HBH · Hu) / 2 | |||
| EM = c5 /(81/2 GH0) | HM | HDE = ln2 Hu | |
| HDM = (tu/tp)2 /2 = Hu /4 | HDM = N | Hmax/HM = 83/2 π2 ln2 | |
| Hmax = 4π2 c5 tu2/(ħG) | Hmax | HBH = (ln2/4) HDE | |
| HBH = (tu/tp)2 /4 | HBH | HBH = [(ln2)2/4] Hu | |
| HBH = N/2 = HDM /2 |
The difference between the calculations according to this formula and formula (2.2) lies in the factor 12π2 = 118.8435. It comes about due to the fact that during the expansion of the cosmos – especially during the period of inflation (see Standard Model of Cosmology) – the volume work pdV has to be considered (see the first law of thermodynamics: dU + pdV = 0) [1].
Conclusion
PLANCK time can be understood as the oscillation period τ. Oscillations are fundamental oscillations of the cosmic space. The dark energy satisfies the Planck/Einstein formula . Dark energy can be interpreted as information flow. According to formula (3.2), the cosmic information multiplied by ln2 is nothing more than the age of the universe in Planck time units squared. The approximately fivefold amount of the currently known total information content of the universe would still have space on the surface of a spherical universe. Dark matter corresponds to the number of AQIs in the cosmos. The information equivalents of dark matter and the total mass energy of the cosmos are in a ratio 1/4. Dark energy and dark matter are in a ratio 2/ln2. The ratio of dark energy to the total mass energy of the cosmos is ln2.
According to the formula (4,5) the ratio Hmax / HM is equal to 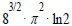 The information equivalent of the black holes
in the cosmos is equal to
The information equivalent of the black holes
in the cosmos is equal to 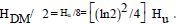 Half of the
hypothetical particles of dark matter are distributed over the black holes in the universe and can be made accessible after the experimental production of small black holes in a particle accelerator.
Half of the
hypothetical particles of dark matter are distributed over the black holes in the universe and can be made accessible after the experimental production of small black holes in a particle accelerator.
These statements can serve only as the beginnings of a theory on dark energy and give cause for further research.
Definition of symbols used in formulas
A = effect, action
AH = area of the black hole event horizon measures the information potentially contained in it
Au = surface of the spherical universe, corresponding to Hu
Ak = surface of the spherical universe, corresponding to Hk
AQI = abstract quantum information (protyposis)
R = cosmic radius
c = speed of light
ν = frequency
E = energy
G = constant of gravitation
H0 = HUBBLE constant
H = SHANNON information entropy
HBH = information equivalent of the total mass energy of the number of black holes in the cosmos
HDE = information equivalent of dark energy
HDM = information equivalent of dark matter
HK = cosmic information, HK = HDE
HNeu = information equivalent of neutrinos
Hu = information equivalent of the total mass energy of the universe
h = PLANCK quantum of action, ħ = h/(2π)
k = BOLTZMANN constant
M = mass
MDM = mass of dark matter
MKG = cosmic total mass
MM = mass of visible baryonic matter
N = number of AQIs in the cosmos
nBH = number of AQIs for a black hole
p = pressure
Q = thermal energy
S = thermodynamic entropy
SH = BEKENSTEIN HAWKING entropy
T = absolute temperature
τ = period of oscillation
t = time
tu = age of the universe
tp = PLANCK time
lp = PLANCK length
U = internal energy
V = volume
zBH = number of black holes in the cosmos (Thomas Gornitz)
References
- Gornitz TH. Quantenkosmologie erklärt die „Dunkle Materie“ sowie die Struktur der Wechselwirkungen und macht die„ Dunkle Energie “überflüssig. 2017.
- Joge F. Information und Wirkung. Zur Einführung des Immanenzbegriffs als physikalische Größe. Grenzgeb Wiss. 2015;64(3):215-28.
- Eigen M. Von der Entropie zur Information-die physikalische Chemie der belebten Materie. Bunsentagung Berlin. Ber Bunsenges Phys Chem. 1994;11:1351-64.
- Tipler PA, Llewellyn RA. Moderne Physik. 2003.
- Ising H. Information and energy. Figshare. 2016.
- Pagel L. Information ist Energie. Definition eines physikalisch begründeten Informationsbegriffs. Springer Fachmedien. 2013;27.
- De BL. La Themodynamique de la particule isolée (ou Thermodynamique cachée desparticules). Found Phys. 1970;1:5-15.
- Gornitz TH. Der kreative Kosmos: Geist und Materie aus Information. Akademie Verlag. 2002;388.
- Bekenstein J. Information in the holographic universe. Sci Am. (2003;289(2):58-65.
- Penrose R. The Emperor`s New Mind. Oxf Univ Press. 1989;480.
- Sedlacek KL. Äquivalenz von Information und Energie. Demand. 2010.
- Tribus M. MC IRVINE, E.C.: Energy and Information. Sci Am. (1971;225(3):179-88.
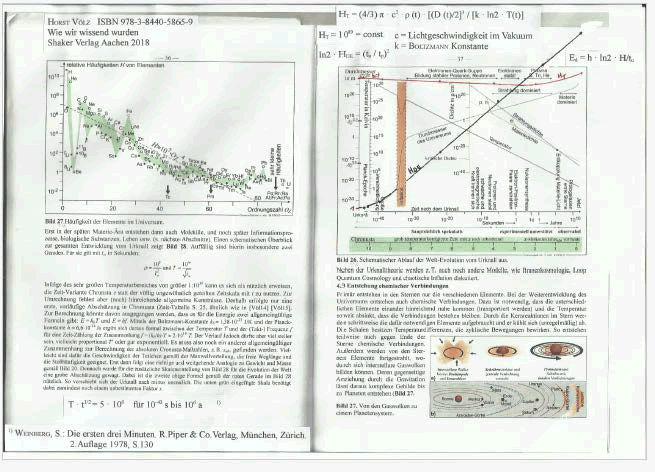
- Volz H. Das ist Information. Aachen: Shak Verl. 2017;372.
- Volz H. Wie wir wissend wurden: Nicht Alles ist Information. Aachen: Shak Verl. 2018;54.