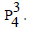Dominating Sets and Domination Polynomials of Cubic Paths
Research Scholar, Department of Mathematics Mother Teresa Women's University, Kodaikanal, India
Received: 21-Sep-2022, Manuscript No. PULJPAM-22-5374; Editor assigned: 23-Sep-2022, Pre QC No. PULJPAM-22-22-5374 (PQ); Accepted Date: Oct 04, 2022; Reviewed: 30-Sep-2022 QC No. puljpam-22-5374 (Q); Revised: 02-Oct-2022, Manuscript No. PULJPAM-22-5374 (R); Published: 20-Oct-2022, DOI: 10.37532/2752-8081.22.6(5).32-35.
Citation: Medona A, Christilda S. Dominating Sets and Domination Polynomials of Cubic Paths. J Pure Appl Math 2022;6(5): 24-27
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
Let G = (V, E) be a simple graph. A set SV ⊆ is a dominating set of G, if every vertex in V – S is adjacent to at least one vertex in S. Let 3 Pn be the cubic path nP and let ( ) 3 n D P , i denote the family of all dominating sets of 3 Pn with cardinality i. Let ( ) 3, n d P i= | ( ) 3 n D P , i |. In this paper, we obtain a recursive formula for 3 n d(P ,i). Using this recursive formula, we construct the polynomial = = ∑ n 3 3i nn i ni 7 (P ) d(P , D,ixi)x which we call the domination polynomial of Pn3 and obtain some properties of this polynomial.
Keywords
Domination Set; Domination Number; Domination Polynomials
Introduction
Mets Let G = (V, E) be a simple graph of order 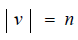 . For any vertex
. For any vertex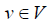 , the open neighborhood of v is the set
, the open neighborhood of v is the set 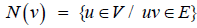 and the closed neighborhood of v is the set
and the closed neighborhood of v is the set 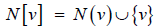 For a set
For a set 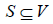 the open neighborhood of S is
the open neighborhood of S is 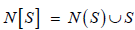 and the closed neighborhood of S is
and the closed neighborhood of S is 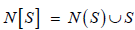 . A set
. A set 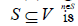 dominating set of G, if N [S] = V , or equivalently, every vertex
dominating set of G, if N [S] = V , or equivalently, every vertex
in V – S is adjacent to atleast one vertex in S. The domination number of
a graph G is defined as the minimum size of a dominating set of vertices in
G and it is denoted by γ (G) . A simple path is a path in which all its internal
vertices have degree two and the end vertices have degree one and is denoted
by 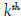
Definition 1
The 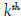 power of a graph is a graph with set of vertices of G and an edge
between two vertices if and only if there is a path of length atmost k between
them. It is denoted by
power of a graph is a graph with set of vertices of G and an edge
between two vertices if and only if there is a path of length atmost k between
them. It is denoted by 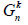 and also called
and also called 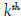 power of G.
power of G.
Definition 2
Let D(G, i) be the family of dominating sets of a graph G with cardinality i
and let 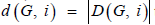 then the domination polynomial D(G, x) of G
then the domination polynomial D(G, x) of G 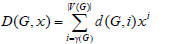 is defined by
is defined by
Where γ (G) is the domination number of G.
Definition 3
The cube of a graph with the same set of vertices as G and an edge between
two vertices and only if there is path of length atmost 3 between them. The
third power of a graph is also called its cube of G [1, 2].
Let 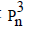 be the cubic of the path Pn (3rd power) with n vertices. Let
be the cubic of the path Pn (3rd power) with n vertices. Let 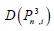 be the family of dominating sets of the graph with cardinality i and let
be the family of dominating sets of the graph with cardinality i and let 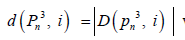 we call the polynomial
we call the polynomial 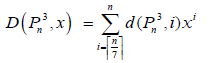
Main Results
Let 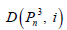 be the family of dominating sets of
be the family of dominating sets of 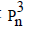 with cardinality i. we
investigate the dominating sets of
with cardinality i. we
investigate the dominating sets of 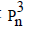 , we need the following lemma to prove
our main results in this section [3].
, we need the following lemma to prove
our main results in this section [3].
Lemma 1
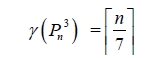
Proof
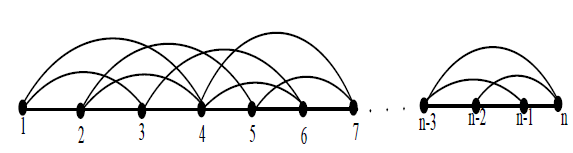
In the proof  any vertex i with 4 ≤ i ≤ n – 3 covers i – 1 and i – 3 in the left side and i + 1 and i + 3 in the right side. Similarly any vertex i with 3 ≤ i ≤ n – 2 covers i – 1 and i – 2 in the left side and i+1 and i+2 right side. Therefore, a single vertex covers atmost 7 vertices Figure 1.
any vertex i with 4 ≤ i ≤ n – 3 covers i – 1 and i – 3 in the left side and i + 1 and i + 3 in the right side. Similarly any vertex i with 3 ≤ i ≤ n – 2 covers i – 1 and i – 2 in the left side and i+1 and i+2 right side. Therefore, a single vertex covers atmost 7 vertices Figure 1.
Therefore 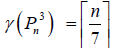
Domination Polynomial of 
Let 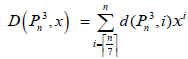 be the domination polynomial of a cubic path
be the domination polynomial of a cubic path 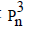 . In this section we derive the expression for
. In this section we derive the expression for 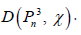
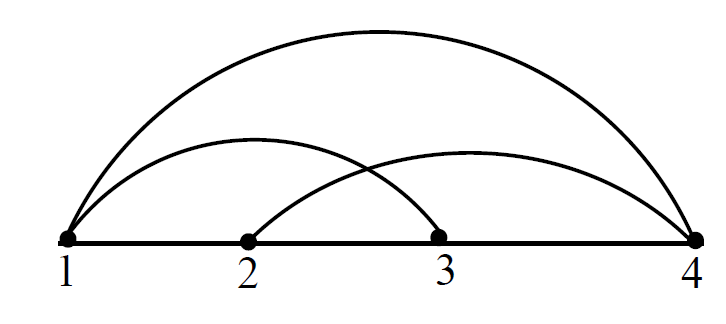
Example 1
The graph 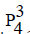 has one dominating set of cardinality 4, 4 dominating set of cardinality 3, 6 dominating set of cardinality 2, 4 dominating set of cardinality 1.
has one dominating set of cardinality 4, 4 dominating set of cardinality 3, 6 dominating set of cardinality 2, 4 dominating set of cardinality 1.
Therefore its domination polynomial is 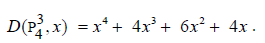
Result
If 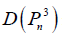 is the family of dominating sets with cardinality i of
is the family of dominating sets with cardinality i of 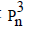 then
then 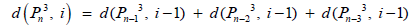
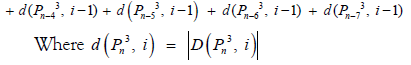
Where 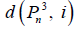
We obtain 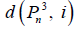 for 1≤ n ≤15 as shown in following table
for 1≤ n ≤15 as shown in following table 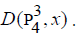 the number of dominating set of
the number of dominating set of 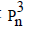 with cardinality i
with cardinality i
In the following theorem we obtain some properties of d (Pn3, i) Figure 2, Table 1.
TABLE 1 In the following theorem we obtain some properties of 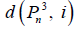
| i> | 1> | 2> | 3> | 4> | 5> | 6> | 7> | 8> | 9> | 10> | 11> | 12> | 13> | 14> | 15> |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n> | |||||||||||||||
| 1> | 1> | ||||||||||||||
| 2> | 2> | 1> | |||||||||||||
| 3> | 3> | 3> | 1> | ||||||||||||
| 4> | 4> | 6> | 4> | 1> | |||||||||||
| 5> | 3> | 10> | 10> | 5> | 1> | ||||||||||
| 6> | 2> | 13> | 20> | 15> | 6> | 1> | |||||||||
| 7> | 1> | 15> | 33> | 35> | 21> | 7> | 1> | ||||||||
| 8> | 0> | 16> | 48> | 68> | 56> | 28> | 8> | 1> | |||||||
| 9> | 0> | 15> | 64> | 116> | 124> | 84> | 36> | 9> | 1> | ||||||
| 10> | 0> | 13> | 78> | 180> | 240> | 208> | 120> | 45> | 10> | 1> | |||||
| 11> | 0> | 10> | 88> | 257> | 420> | 448> | 328> | 165> | 55> | 11> | 1> | ||||
| 12> | 0> | 6> | 92> | 341> | 676> | 868> | 776> | 433> | 220> | 66> | 12> | 1> | |||
| 13> | 0> | 3> | 88> | 423> | 1012> | 1543> | 1644> | 1269> | 653> | 286> | 78> | 13> | 1> | ||
| 14> | 0> | 1> | 78> | 491> | 1420> | 2549> | 3186> | 2913> | 1922> | 939> | 364> | 91> | 14> | 1> | |
| 15> | 0> | 0> | 64> | 536> | 1876> | 3948> | 5728> | 6098> | 4835> | 2861> | 1303> | 455> | 105> | 15> | 1> |
Theorem 1
The following properties hold for the coefficient of 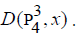
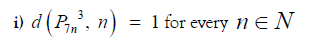
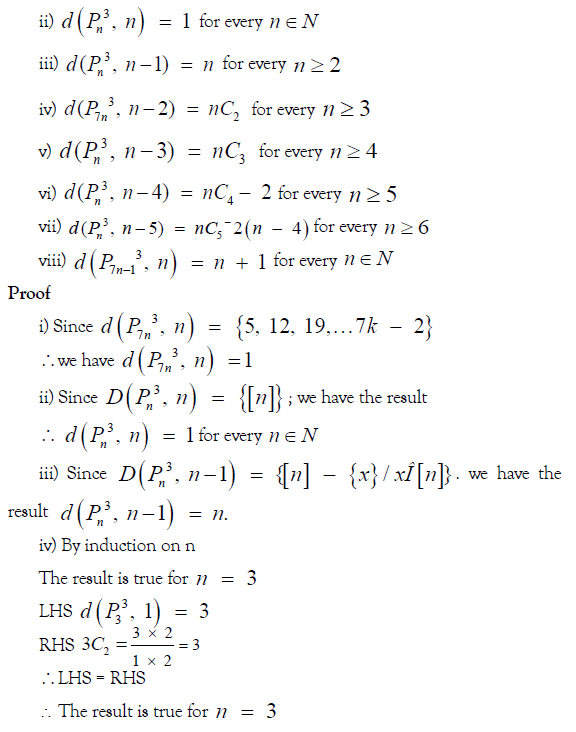
Now suppose that the result is true for all numbers less than ‘n’ and we prove it for n.
By result 3.2,
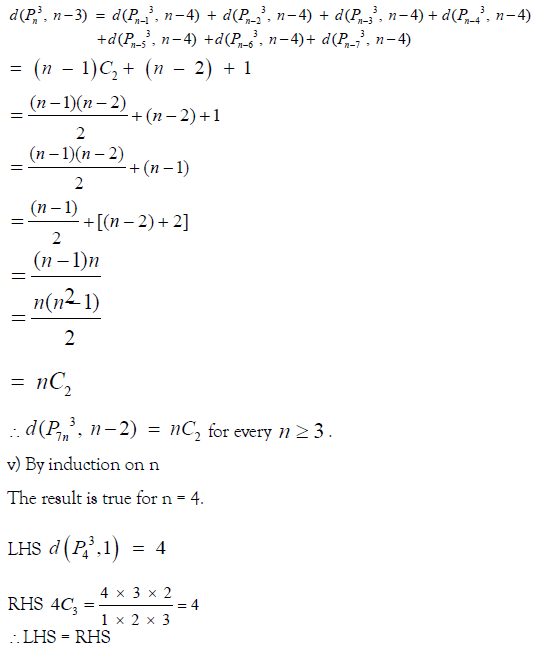
∴ The result is true for n = 4.
Now suppose that the result is true for all numbers less than ‘n’ and we prove it for ‘n’
By result 3.2,
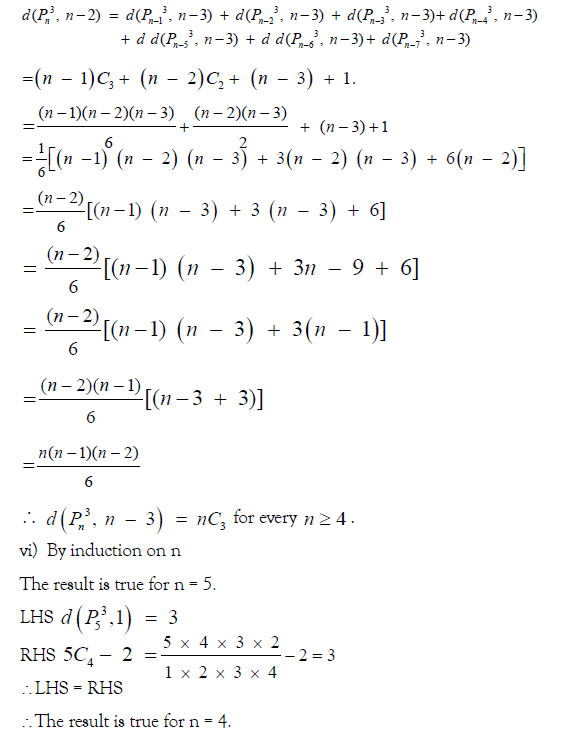
Now suppose that the result is true for all numbers less than ‘n’ and we prove it for ‘n’ by result 3.2,
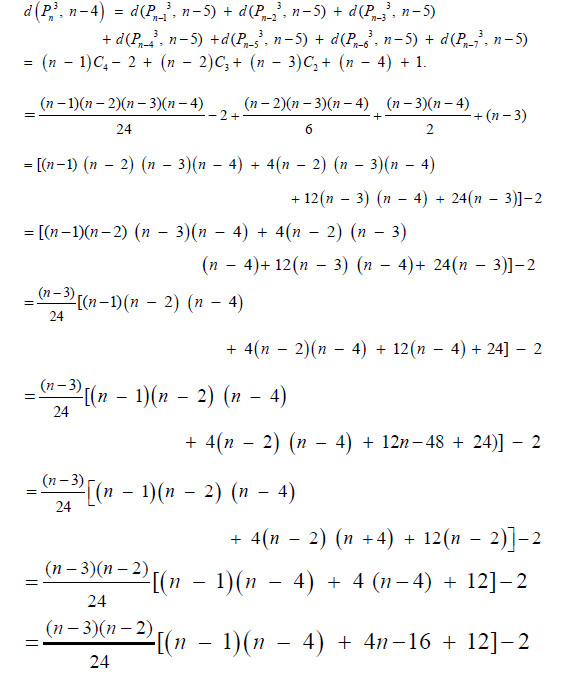
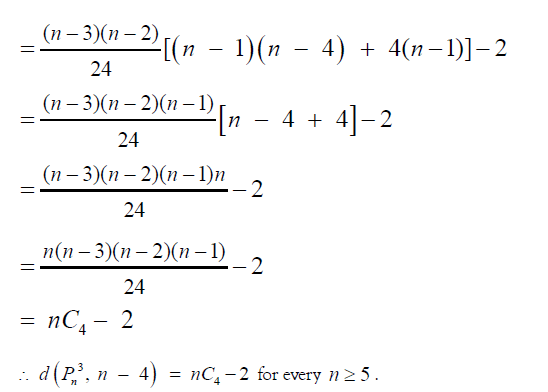
vii) By induction on n
The result is true for n = 6.
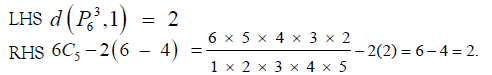
∴LHS = RHS
Now suppose that the result is true for all numbers less than ‘n’ and we prove it for n.
By result 3.2,
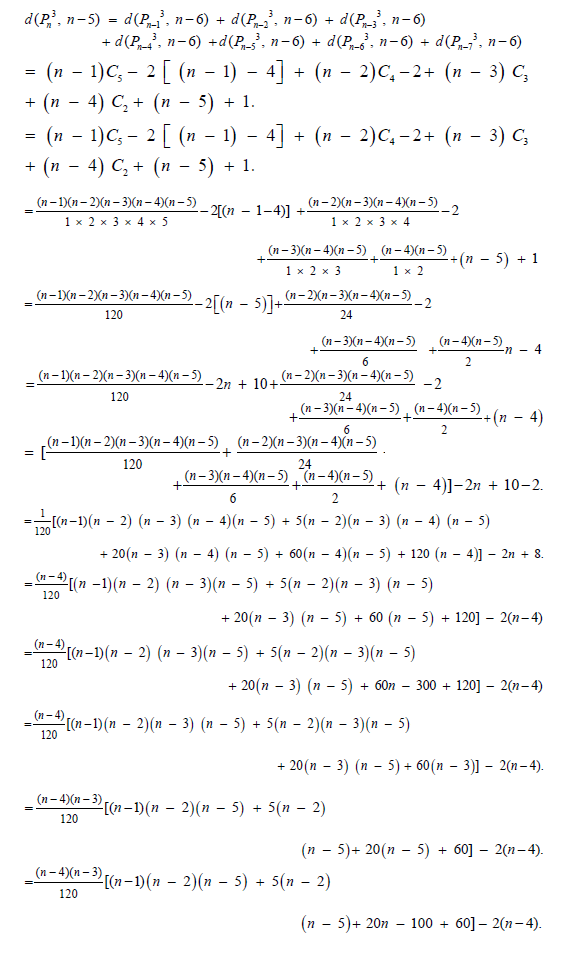
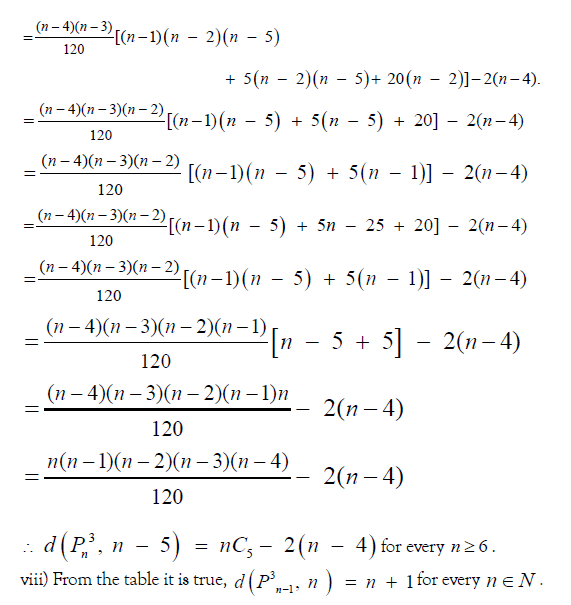
Theorem 2
Proof by induction on n,
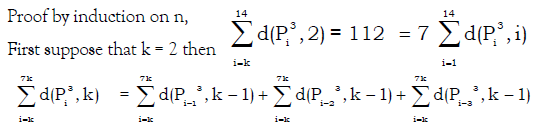
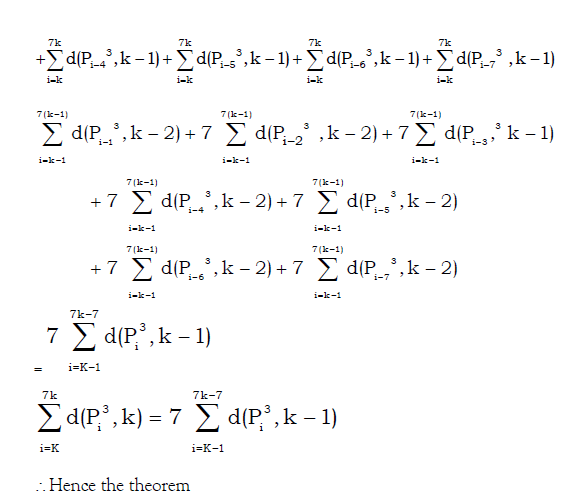
Conclusion
Using domination Polynomial, we obtain many interesting properties and theorems. This study can be expanded to other graphs also.
References
- Alikhani S, Peng H. Introduction to Domination Polynomial of a Graph. arXiv preprint. 2009.
- Alikhani S, Peng H. Domination Sets and Domination Polynomials of Paths. Int J math Math Sci. 2009;1:1.
- Vijayan A. Gipson K. Dominating sets and Domination Polynomials of square of Paths. Open J Discrete Math. 2013;3(1):60-9.