Elementary matrix algorithm of order 3

Received: 02-Apr-2024, Manuscript No. puljpam-24-7013; Editor assigned: 06-Apr-2024, Pre QC No. puljpam-24-7013(PQ); Accepted Date: May 27, 2024; Reviewed: 25-Apr-2024 QC No. puljpam-24-7013(Q); Revised: 30-Apr-2024, Manuscript No. puljpam-24-7013(R); Published: 31-May-2024, DOI: 10.37532/2752- 8081.24.8(3).01-02

Citation: Pozinkevych R. Elementary matrix algorithm of order 3. J Pure Appl Math. 2024; 8(3):01-02.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

The aim of our research is to establish relationship between linearly independent vectors and the R³ space. The means for that are going to be taken from balanced ternary analysis e.g. triplets with entries (-1,0,1). This is not going to be any specific vector, for instance (-1,0,1) It’s going to be rather a coordinate system with 8 quadrants and directional vectors. The novelty of the proposed research lies in the fact that unlike traditional Cartesian system-vector basis our system uses 8 vectors which are at the same time a polyvector (Boas). We may define it as a multiple of the type: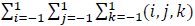

Key Words

Eigenvector; Eigenvalue; Ternary basis

Introduction

Let’s see how the proposed algorithm works for a decimal system. For the real numbers, n∈, n can be expressed as a determinant of a matrix of order 3 which in its turn can be presented as 3 rows of three component vectors 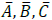which can be related in terms ofcombination of the three parts: 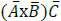[1-3].

For us an important thing would be to present each component of the formula 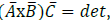as an algorithm. For this reason, we haveto remind ourselves of some postulates of matrix algebra.

One of them is saying that a determinant of the matrix depends of the coefficient (We are talking about square matrices of course). In other words

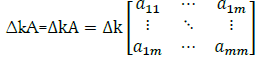
Our interest is 3х3 matrix. The reason for that was in the formula mentioned earlier, namely: 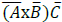[4].

The three vectors could be placed in the form of a matrix

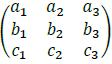
The only condition is that are linearly independent [5].

To obtain a matrix of three row entries representing linear independence of vectors we are going to apply our ternary algorithm:

Step 1

Rewrite the first row two times as the entry of the first and the second row.

Step 2

Make second row entries equal x,y,z:

| x = b₁ = a₁; y = b₂ = a₂; z = b₃ = a₃;

The matrix now should look like this:

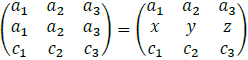
Rewrite the first row as the entry of the second row

Step 3

Make the entries of the third row equal (-1,0,1) respectively:

| c₁ = 1; c₂ = -1; c₃ = 0;

Step 4

The dot product of (x,y,z)∙ (-1,0,1) should effectively replace our second raw entry by the vector a₁;-a₂; 0;

Our matrix entries now look as follows:

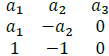
Step 5

Now it’s high time to make our matrix entries equal the determinant Δ

Equalize or place both entries on left and right sides of the equation:

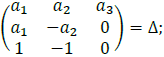
Step 5

The final step of the sought-after algorithm.

Conclusion

Now the question arises as to what did one accomplish by developing the following algorithm?

To answer that we must dig into the basics of discrete mathematics and linear algebra. When it comes to the Descartes system of coordinates the answer is simple. All you need to care about is ordered pairs. In the affine system we use the change of basis (In our example it was the third row of entries which is used as a final step to calculate the determinant or in simple words to place our vector product in correspondence with real numbers which in its own turn places.

To prove our theory, we can use the transpose of the resultant matrix and make sure that the determinant has not changed.

What about other entries? Well, we have 27 combinations of the entries making it possible to solve systems of equations in 27 bases. That in itself empowers encoding and decoding of data as far as digits are concerned. More importantly though is to be able to introduce an alternative system of counting and the algorithm that goes with it.

References

1. Bonanzinga V. Some applications of linear algebra and geometry in real life. ArXiv. 2022.

   [Google Scholar] [CrossRef]

2. Hošková-Mayerová Š, Flaut EC, Maturo F, et al. Algorithms as a Basis of Modern Applied Mathematics. Springer. 2021.

   [Google Scholar] [CrossRef]

3. Pozinkevych R. Logical Principles in Ternary Mathematics. Asi J Res Comp Sci. 2021;7(3):49-54.

   [Google Scholar] [CrossRef]

4. Strang G. Introduction to linear algebra. Wellesley-Cambridge Press. 2022.

   [Google Scholar]

5. Sieg W, Ravaglia M. David Hilbert, et al. InLandmark Writings in Western Mathematics. Elsevier. 2005. 981-99.

   [Google Scholar] [CrossRef]