First occurring singularities of functions on symplectic semi-space

Received: 30-Apr-2018 Accepted Date: May 10, 2018; Published: 15-May-2018, DOI: 10.37532/2752-8081.18.2.7

Citation: Kourliouros K, Zhitomirskii M. First occurring singularities of functions on symplectic semi-space. J Pur Appl Math. 2018;2(2):11-13.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

We explain how the classical theorem by Arnol’d and Melrouse on non-singular functions on a symplectic manifold with a boundary can be proved in few lines, and we use the same method to obtain a new result, which is a normal forms with functional invariants for the first occurring singularities.

Keywords

Symplectic semi-space; Singularities; Functional moduli

All objects in the paper are either C∞ or analytic germs at 0. By a symplectic semi-space we mean the symplectic space (ℝ²ⁿ ,ω) where ω is a symplectic form, endowed with a smooth hypersurface , which can be interpreted as the boundary. The Darboux-Givental’ theorem [1] implies that all symplectic semi-spaces are locally equivalent. We deal with the problem of classification of functions f on a symplectic semi-space (ℝ²ⁿ,ω,). Two function germs are called equivalent if they can be brought one to the other by a local symplectomorphism of (ℝ²ⁿ,ω) which preserves the hypersurface . An equivalent problem is the classification of triples (ω,, f ) with respect to the whole group of local diffeomorphisms. Notation. In what follows f and h are function germs such that

f (0) = (0), and

h(0) = (0), dh ≠ 0, = {h = 0}. (1.1)

Definition:

The triple (ω, , f ) is non-singular if { f , h}(0) ≠ 0.

Here and in what follows {.,.} is the Poisson bracket with respect to ω.

Theorem 1:

(Melrose [2], Arnol’d [3]). Any non-singular triple (ω, , f ) on ℝ²ⁿ is equivalent to

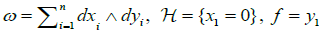. (1.2)

In (2) and (3) the proofs are given without details, but in fact Theorem 1.1 is a simple corollary of the Darboux theorem on odd-symplectic (or quasisymplectic) forms, and we find worth to give a very short proof in section 3; the proofs of our much more difficult theorems on singular (ω, , f ) are based on the same approach.

The paper is devoted to first occurring singularities of (ω, , f ) on ℝ²ⁿ .

Definition:

By S₁ we denote the singularity class consisting of (ω, , f ) such that

for n =1: { f ,h}(0), { f ,{ f ,h}}(0) ≠ 0;

for n¡ :Ý { f , h}(0) = 0, { f ,{ f , h}}(0) ≠ 0, {h{ f , h}}(0) ≠ 0, df ∧ dh(0) ≠ 0.

It is easy to check that the choice of h in (1.1) in the given definitions is irrelevant: if they hold for h then they also hold for Qh where Qis any non-vanishing function. The difference in the definition of S1 for n =1and n ≥ 2 is explained as follows: it is easy to see that for n =1 the assumptions { f , h}(0) = 0,{ f ,{ f , h}}(0) ≠ 0 imply that {h,{ f , h}}(0) ≠ 0 and (df ∧ dh)(0) = 0.

The problem of classification of triples (ω, , f )∈S₁ was raised by R. B. Melrose in (2) where he studied a tied problem of classification of triples (ω, , f ), = {h = 0},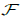 = { f = 0}where and 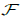are two smooth hypersurfaces and ω is a symplectic form. Melrose studied the first occurring singularities of such triples, called glancing hypersurfaces in a symplectic space, which are distinguished by the same conditions as in the definition of S₁. The main theorem in [2] states that in the C∞ category the glancing hypersurfaces in the symplectic space ℝ²ⁿ⁺² can be described by the normal form

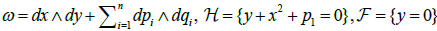. (1.3)

(without dp_i ∧ dq_i in ω and without p₁ in for n = 0 ). In (2), p. 176 he noticed that replacing the hypersurface 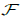by a function f makes the problem substantially different - starting from the first occurring singularities moduli occur. Melrose claimed, and left to the reader to check, that in the family of triples

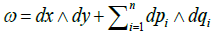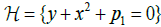, , f = sy (1.4)

the parameter s is an invariant.

The problem of classifying singularities of (ω, , f ) is tied with a number of other classification problems, many of them were solved (a good part - by V. I. Arnol’d and his school, c.f. (1,3). Nevertheless, the problem of classification of singularities of functions in a symplectic semi-space remains, as we know, open. The purpose of this paper is to fill in this gap.

Theorem 1.2:

Any triple 1 (ω, , f )∈S on ℝ² can be brought to the normal form

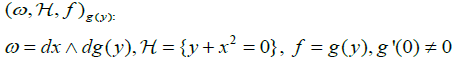. (1.5)

The triple (1.5) is equivalent to 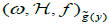if and only if .

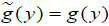We have a functional invariant - a function of one variable g(⋅). In [4] the functional invariant was constructed in a canonical (coordinate-free) way using powerful tools from Gauss-Manin theory. In the same paper another normal form

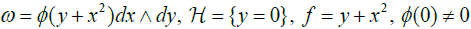(1.6)

with the functional invariant φ (⋅) was obtained. Note that (1.6) can be easily obtained from (1.5) and the proof of (1.5) in section 3 is elementary and takes just few lines.

Theorem 1.3: In the space of (2n) − jets of triples 1 (ω, , f )∈S on ℝ²ⁿ+2 ,n ≥1, , there exists an open set U such that any triple (ω, , f )∈S₁ with j²ⁿ (ω, , f )∈U can be brought to the normal form :

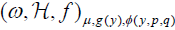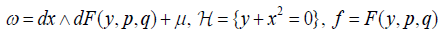(1.7)

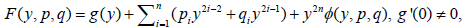
where μ is a symplectic 2-form on 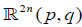. The triple (1.7) is equivalent to 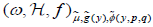if and only if.

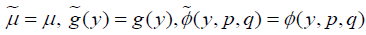In both normal forms (1.5) and (1.7) the numerical invariant g '(0) has a simple canonical meaning by the following lemma.

Proposition 1.4: In the classification of triples 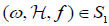the following number k is an invariant:

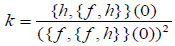
In terms of normal forms (1.5) and (1.7) one has .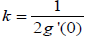

Proof: Using that h(0) = 0 and { f , h}(0) = 0 it is easy to see that when multiplying h by a non-vanishing function Q one has { f ,{ f , h}}(0)→Q(0){ f ,{ f , h}}(0) and {h,{ f ,h}}(0)→Q(0){h,{ f , h}}(0). It follows that does not depend of the choice of h. The formula 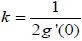can be easily computed.

Remark: Due to Lemma 1.4 we can do Melrose’s homework: the invariant k in his example (1.4) is equal to 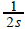, where g ' = 0. Theorems 1.2 and 1.3 are proved, along with much simpler and known Theorem 1.1, in the same way in section 3. The proofs are very short provided that one uses the two lemmas in section 2, the proof of each one of them occupying only a few lines. Probably the reader would ask why we do not use the normal form 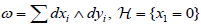for the pair (ω, ) which seems a natural way to obtain normal forms for (ω, , f ) by normalizing the function f with respect to local diffeomorphism preserving this normal form. One can check that this way leads to very involved computations, and even if the computational obstacles can be resolved the proof would be very long.

Auxiliary lemmas

Definition:

A local odd-symplectic form on 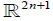is the germ 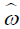at 0 of closed 2 − form 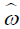such that.

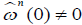In the following lemma and it proof

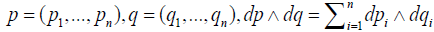. (2.1)

Lemma 2.1:

Any odd-symplectic form 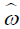on 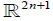( y, p, q) such that 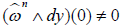can be brought to the form dp ∧ dq by a local diffeomorphism preserving the coordinate y. If Ψ is a local diffeomorphism of 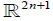( y, p, q) which preserves dp ∧ dq and the coordinate y then Ψ: ( y, p, q)→( y, A( p, q), B( p, q)) where ( p,q)→(A, B) is a local symplectomorphism of .

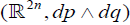Proof:

By the classical Darboux theorem for odd-symplectic forms (the proof can be found, for example, in [5]) 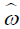can be brought to dp ∧ dq by some local diffeomorphism Φ. This diffeomorphism brings y to a function Y( y, p, q); the assumption 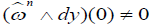implies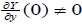. The local diffeomorphism ( y, p, q)→(Y, p, q) brings Y( y, p, q) to y and preserves dp ∧ dq. It proves the first statement. To prove the second statement it suffices to note that any diffeomorphism which preserves both y and the line field 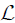generated by 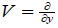has the form given in the lemma, and that 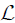is invariantly related to 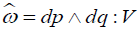is defined, up to multiplication by a function, by 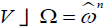where Ω is a volume form.

Lemma 2.2:

Let Z be a non-singular vector field on 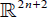which has the simple tangency with a smooth hypersurface . In suitable local coordinates 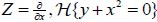. Any local diffeomorphism of 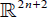which preserves this normal form preserves the coordinates x and y.

Proof:

The given normal form is well-known, see for example [6]. Let us prove the second statement. Any local diffeomorphism preserving the vector field 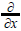change x to x + A( y, p, q) and y to B( y, p, q). It preserves the hypersurface (x + A)² + B if and only if the function (x + A)² + B vanishes on the hypersurface y = −x². It means x² + B(−x² , p, q) + A² (−x² , p, q) + 2xA(−x² , p, q) ≡ 0.Taking the even and the odd part with respect to x we obtain A = 0, B = y.

Proof of Theorems 1.1, 1.2, 1.3

In what follows we denote by Z_f the Hamiltonian vector field defined by f :

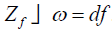(3.1)

We use the coordinates x, y in the 2-dim case. For higher dimensions we work on (x, y, p, q) and we use notations (2.1).

Lemma 3.1:

Let 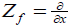. Then in the same coordinates in the 2-dim case f = g( y), ω = dx ∧ dg( y) for higher dimensions: 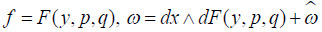(3.2)

where 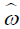is an odd-symplectic form on 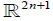( y, p, q).

Proof:

The given form of f follows from the equation Z_f (f) = 0which is a corollary of (3.1) with 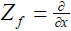. This equation also implies ω = dx ∧ dg( y) for n = 0 and 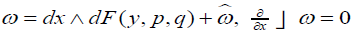for n ≥1. Since dω = 0 and 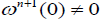it follows that 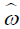is an odd-symplectic form.

Proof of Theorem 1.1:

The condition { f , h}(0) ≠ 0 means that Z_f is transversal to . Take coordinates in which 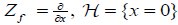. By Lemma 3.1, ω and f have form (3.2). Changing the coordinate y and using Lemma 2.1 we obtain (1.2), up to notations of the coordinates.

Proof of Theorem 1.2:

The conditions { f , h}(0) = 0, { f ,{ f , h}}(0) ≠ 0 mean that Z_f is a non-singular vector field which has the simple tangency with . By Lemma 2.2 the pair 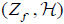can be brought to the normal form 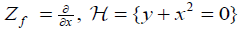. By Lemma 3.1, ω and f have form ω = dx ∧ dg( y), f = g( y) so that we have normal form (1.5) for the triple (ω, , f ).The fact that g( y) is a functional invariant is a direct corollary of the second statement of Lemma 2.2.

Proof of Theorem 1.3:

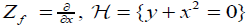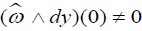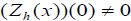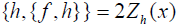As in the proof of Theorem 1.2, we take coordinates in which , and by Lemma 3.1, ω and f have form (3.2). Now we will show that the condition {h,{ f , h}}(0) ≠ 0 in the definition of the singularity class S1 is equivalent to . Let h = y + x². Let Z_h be the Hamiltonian vector field defined by h. The condition {h,{ f , h}}(0) ≠ 0 means . Indeed, since we have { f , h} = 2x and . To find 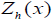we have by definition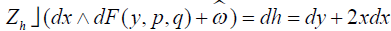. Express this equation in the form

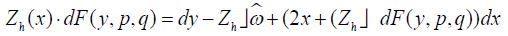(3.3)

Since 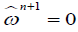we have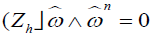. Therefore taking the external product of (3.3) with 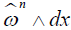we obtain 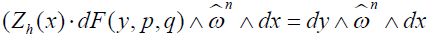and it follows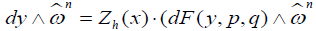. Since 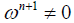we have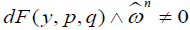. Therefore the condition 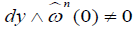is the same as 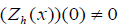which, as is shown above, is the same as {h,{ f ,h}}(0) ≠ 0.Now we can use Lemma 2.1 which allows to bring to dp ∧ dq preserving and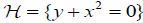. We obtain the normal form

:

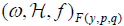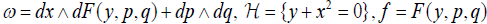. (3.4)

The next step is using the second statements of Lemmas 2.1 and 2.2. They imply that 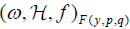is equivalent 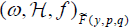if and only if the functions F( y, p, q) and 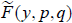can be brought one to the other by a symplectomorphisms of 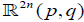. Therefore reducing (3.4) to exact normal form is the same problem as classification of functions F( y, p, q) with respect to symplectomorphisms of 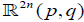. An equivalent problem is as follows: (*) classification of pairs (μ, F( y, p, q)) where μ is any symplectic form on 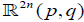with respect to all diffeomorphisms of the form ( y, p, q)→( y,Φ( p, q),Ψ( p, q)).

Let 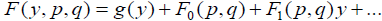where 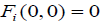. Assuming that the functions 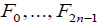are differentially independent at 0, which defines the open set U in Theorem 1.3, we obtain, in the problem (*), the exact normal form with 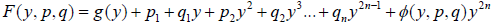where g( y) and φ ( y, p, q) are functional invariants, and the symplectic form μ in the pair (μ, F( y, p, q)) is a functional invariant too. This exact normal form leads to the exact normal form (1.7).

Acknowledgement

The work of both authors was supported by the Israel Science Foundation grant 510/12. AMS Subject classi_cation: 53D05, 58K50.

REFERENCES

1. Arnol'd VI, Novikov SP. Symplectic Geometry and its Applications. Springer Verlag. 1990.
2. Melrose RB. Equivalence of glancing hypersurfaces. Inventiones Mathematicae. 1976;37:165-91.
3. Arnol'd VI. Lagrangian manifolds with singularities, asymptotic rays, and the open swallowtail. Functional Analysis and Its Applications. 1981;15:235-246.
4. Kourliouros K. Gauss-Manin Connections for Boundary Singularities and Isochore Deformations. Demonstratio Mathematica. 2015;48:250-288.
5. Zhitomirskiĭ M. Typical singularities of differential 1-forms and Pfaffian equations. American Mathematical Soc. 1992.
6. Arnol'd VI, Varchenko A, Gusein-Zade S. Singularities of dfferentiable maps vol. I, Monographs in Mathematics, Birkhauser. 1998.