Fredoholm integral equation based on Bernstein polynomials in each finite section

Received: 18-Feb-2022, Manuscript No. puljpam-22-4729; Editor assigned: 21-Feb-2022, Pre QC No. puljpam-22-4729(PQ); Accepted Date: Mar 17, 2022; Reviewed: 08-Mar-2022 QC No. puljpam-22-4729(Q); Revised: 17-Mar-2022, Manuscript No. puljpam-22-4729(R); Published: 18-Mar-2022, DOI: 10.37532/2752- 8081.22.6.2.3-4

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

Integral equations are widely used in many physical models appearing in the fields of plasma physics, atmospheric-ocean dynamics, fluid mechanics, mathematical physics, and many other branches of physics. and science and technology. In this work, a new digital technique for solving systems of Fredholm Integral Equations (FIEs) of the first and second types is established, based on Bernstein basis functions. Here, the FIE system of both types has been taken and then reduced to an algebraic linear system that can be solved using any of the standard rules. Convergence analysis of the proposed technique and some useful numerical results are presented so that the reader can easily understand the idea. In addition, the HyersUlam stability analysis criterion was used to analyze the stability of the proposed technique.

Commentary

The mathematical form of physical models leads mainly to FIEs. FIE occurs in various physical and engineering models such as signal processing, linear direct modeling, polymer mass distribution in molten polymers, and more. Over the past decades, many techniques have been presented by different authors for the solution to FIE. Babolian et al. applied the analytical method to solve linear FIEs of the second kind. Vahidi and Mokhtari proposed a decomposition method for a system of linear FIEs of the second kind. They show that Adomian's method of decay is equivalent to Picard's method. Rashidinia and Zarebnia described the convergence of the approximate solutions of the FIE where the numerical solution was obtained by the method of Sinccollocation. This technique converts a system of integral equations into an explicit algebraic system of equations. The Taylor extension method was presented by Maleknejad et al. With a smooth or weak singular kernel to solve FIEs of the second kind. Furthermore, the modified isotope perturbation method was introduced by Javidi to find the system of linear FIEs. Khan et al. introduced a new computational multi-parameter isomer approach for systems of linear EIPs. In fact, it is a modified method to form an improved isomorphism and contains three convergence control parameters. Muthuvalu and Sulaiman presented a half-scan averaging method to solve FIEs based on the composite trapezoidal rule. They tested the effectiveness of the HalfSweep arithmetic mean method for solving dense linear systems. Khan et al. presented a custom technique to solve mixed Volterra-Fredholm integral equations and 2D Volterra integral equations from mathematical physics. Furthermore, the feedback neural network (NN) approach was used by Jafarian and Measoomy to find approximate solutions for the FIEs. Taylor expansions have also been proposed for various methods to solve different types of integral equations. In recent years, many methods based on fractional mathematics, system dynamics, and superstrange behavior of the involuntary cardiac conduction system have been proposed to find numerical solutions for several tissues. certain physical form. In view of the literature, no attempt has been made to solve a FIE system of the first kind by any technique. Furthermore, the proposed technique has not yet been used for FIE systems of both types over arbitrary time intervals [a,b]. The main aspiration here is a series of applied problems whose natural mathematical framework is an integral equation, so they have the advantage of a simple solution method. In this technique, the desired precision can be achieved by increasing the order of the Bernstein polynomial. As increasing the degree increases the computational cost, a new method is presented using Bernstein polynomial to solve FIEs of the first and second type in arbitrary time intervals [a,b] as we can obtain precision required at the lower level of the polynomial.

The FIE system of the first type has the form

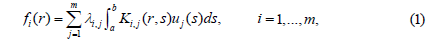
The system of FIEs of the second kind is of the form

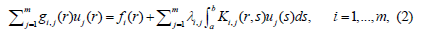
aim of this work is to use Bernstein polynomials for solving systems of FIEs. This paper consists of the following sections: Describes some results and the basic concept of Bernstein polynomials. In the general method is explained. Shows the convergence analysis of the given technique. Hyers Ulam stability of the proposed numerical technique is given. In examples and numerical results are provided to verify the effectiveness of the given technique. The exact and approximate solution comparisons are also given and graphed. Finally, includes the conclusion and follow-up work.

Conclusion

Integral equations have had a rich background in physics in recent years. These equations have aroused great interest in many disciplines and are widely used in dynamical systems with chaotic behavior and in nearly chaotic dynamical systems. The use of Bernstein polynomials to solve initial value problems, boundary value problems, and integral equations has recently increased due to fast convergence and lower computational costs. In this study, the main topic is to provide a technique with fast convergence and lower computational cost for the solution of the first and second type FIEs on arbitrary time intervals [a,b]. We find that the proposed method gives excellent approximations even when taking a small value of order n. The proposed technique can be extended to numerical solutions of two-dimensional integral and differential equations appearing in engineering models, but some adjustments will be needed.