Involutive Hom-Lie triple systems

Received: 30-Mar-2018 Accepted Date: Apr 06, 2018; Published: 09-Apr-2018, DOI: 10.37532/2752-8081.18.2.5

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

In this work we we prove that all involutive Hom-Lie triple systems are whether simple or semi-simple. Moreover, we prove that an involutive simple Lie triple system give a rise of InvolutiveHom-Lie triple system.

Keywords

Jordan triple system; Lie triple system; Casimir operator; Quadratic lie algebra; TKK construction

The classification of semisimple Lie algebras with involutions can be found in [1]. The Hom-Lie algebras were initially introduced by Hartwig, Larson and Silvestrov in [2] motivated initially by examples of deformed Lie algebras coming from twisted discretizations of vector fields. The Killing form K of g is nondegenerate and 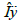is symmetric with respect to K. In [3], the author studied Hom-Lie triple system using the double extension and gives an inductive description of quadratic Hom-Lie triple system. In this work we recall the definition of involutive Hom-Lie triple systems and some related structure and we prove that all involutive Hom-Lie triple systems are whether simple or semi-simple. Moreover,we prove that an involutive simple Lie triple system give a rise of Involutive Hom-Lie triple system.

Definition 0.1

A Hom-Lie triple system is a triple (L,[−,−,−],α) consisting of a linear space L, a trilinear map [−,−,−]: L× L× L→ L and a linear map α : L→ L such that

[x, y, z] = 0 (skewsymmetry)

[x, y, z]+[ y, z, x]+[z, x, y] = 0 (ternary Jacobi identity) [α (u),α (v),[x, y, z]] = [[u,v, x],α ( y),α (z)]+[α (x),[u, v, y],α (z)]+[α (x),α ( y),[u, v, z]],

for all x, y, z,u,vε L. If Moreover α satisfies α ([x, y, z]) = [α (x),α ( y),α (z)](resp. 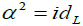) for all x, y, zε L, we say that (L,[−,−,−],α ) is a multiplicative (resp. involutive) Hom- Lie triple system.

A Hom-Lie triple system (L,[−,−,−],α ) is said to be regular if α is an automorhism of L.

When the twisting map α is equal to the identity map, we recover the usual notion of Lie triple system [4,5]. So, Lie triple systems are examples of Hom- Lie triple systems. If we introduce the right multiplication R defined for all x, yε L by R(x, y)(z) := [x, y, z], then the conditions above can be written as follow:

R(x, y) = −R( y, x),

R(x, y)z + R( y, z)x + R(z, x) y = 0,

R(α (u),α (v))[x, y, z] = [R(u,v)x,α ( y),α (z)]+[α (x), R(u, v) y,α (z)]+[α (x),α ( y), R(u, v)z]. We can also introduce the middle (resp. left) multiplication operator

M(x, z)y := [x, y, z](resp.L(y, z)x := [x, y, z]) for all x, y, zε L.The equations above can be written in operator form respectively as follows:

M(x, y) = −L(x, y) [1]

M(x, y) −M( y, x) = R(x, y) for all x, yε L. [2]

We can write the equation above as one of the equivalent identities of operators:

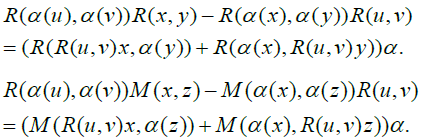
Definition 0.2

Let (L[−,−,−],α ) and (L',[−,−,−]',α ') be two two Hom-Lie triple systems [6]. A linear map f : L→ L' is a morphism of Hom-Lie triple systems if 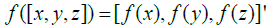and .

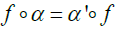In particular, if f is invertible, then L' and L'are said to be isomorphic.

Definition 0.3

Let (L,[−,−,−],α be a Hom-Lie triple system and I be a subspace of L. We say that I is an ideal of L if [I , L, L]⊂ I and α (I ) ⊂ I.

Definition 0.4

A Hom-Lie triple system L is said to be simple (resp. semisimple) if it contains no nontrivial ideal (resp.Rad(L) = {0}).

According to a result in [ ? ], if A is aMalcev algebra, then (A,[−,−,−]) is a Lie triple system with triple product

[x, y, z] = 2(xy)z − (zx) y − ( yz)x. [3]

Thus, if A is aMalcev algebra and α : A→ A is an algebra morphism, then, 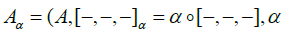is a multiplicative Hom-Lie triple system, where [−,−,−] is the triple product in [3].

Proposition 0.5

Let L be a Lie triple system and α be an automorphism of L. If L is simple, the L is also simple.

Proof: Since L is not abelian, then Lα is also not abelian. Moreover, let I be an ideal of Lα . For all x, yε L and a aε I we have,

[a, x, y]_αεI.

That is,

[α (a),α (x),α ( y)]ε I.

Consequently, I is an ideal of L because α is an automorphism. Thus, I = {0}.

Theorem 0.6

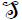Let (L,[.,.,.],θ ) be an involutiveHom-Lie triple system. Then, (L,[.,.,.],θ ) is simple or semi-simple. Moreover, in the second case L can be wrien as where is a simple ideal of L. Conversely, If (L,[.,.,.],θ ) is an involutive simple Lie triple system, then (L,[.,.,.]_θ, θ ) is an involutive Hom-Lie triple system.

Proof: Suppose that L_θ is not simple and put a minimal ideal of L_θ . We get 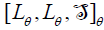is an ideal of L_θ which is contained on 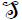. Thus, 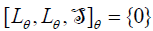or .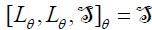

Now, firstly, if 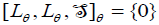, then 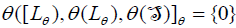. That is, 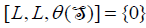, because θ is a bijective linear map. which mean that 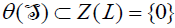.Thus, 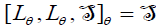. Hence, 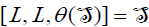. Which implies that 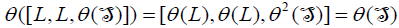.Consequently, .

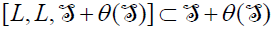Furthermore,

.

Thus 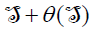is an ideal of (L,[.,.,.],θ ). Since 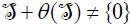, then .

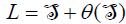Now, we have to prove that the summation is direct. In fact, since θ is an automorphism of L_θ, then 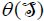is an ideal of L_θ. Thus, 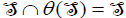or 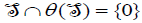because 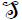is minimal. Suppose that 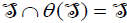then 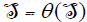because θ is bijective. On the other hand,

.

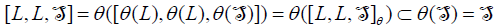Thus, 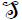is an ideal of (L,[.,.,.],θ ) and 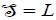because (L,[.,.,.]) which contradict the fact that and 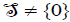.Consequently, 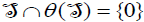and .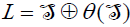

Let us prove that 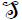is a simple ideal of (L_θ,[.,.,.]_θ). In fact, 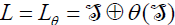. Since θ is an automorphism of L then θ is an automorphism of L_θ.

.

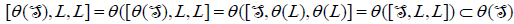Thus, 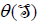is an ideal of L_θ. Furthermore,

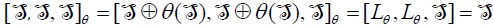. Thus, 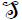is a simple ideal of L_θ because it is simple with 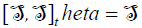. Consequently, L_θ is semi-simple.

Corollary 0.7

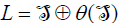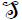Let (L,[.,.,.]) be a Lie triple system with involution θ. Such that, where is a simple ideal of (L,[.,.,.]). Then the Hom-Lie triple system 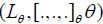is simple.

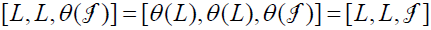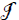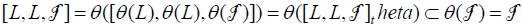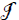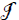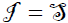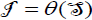Proof: Let be an ideal of L_θ such that .We have because L =θ (L) and is an ideal of L_θ. Moreover, , because is stable under θ since it is an ideal of the Hom-Lie triple system of L_θ. Consequently, is an ideal of L. Thus, or or 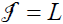. Since 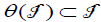, then 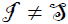and 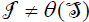.Thus, .

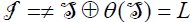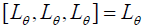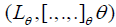Moreover, since [L, L, L] = L, then Thus is a simple Hom-Lie triple system.

REFERENCES

1. Lister WG. A structure theory of Lie triple systems. Trans Am Math Soc. 1952;72:217-242.
2. Hartwig JT, Larsson D, Silvestrov SD. Deformations of Lie algebras using σ-derivations. J Algebra 2006;295:314-361.
3. Baklouti A. Quadratic Hom-Lie triple systems. J Geom Phys. 2017;121:166-175.
4. Meyberg K. Lectures on algebras and triple systems. University of Virginia. 1972.
5. Jacobson N. Lie and Jordan triple systems. Amer J Math. 1949;71:149-170.
6. Benayadi S, Makhlouf A. Hom-Lie algebras with symmetric invariant nondegen-erate bilinear forms. J Geom Phys. 2014;76:38-60.