Iterative solutions for variational inclusion problems in Banach spaces

Received: 06-Jun-2021 Accepted Date: Jun 08, 2021; Published: 16-Jun-2021, DOI: 10.37532/2752-8081.21.5.35

Citation: Anyaiwe OED, Moore C. Iterative solutions for variational inclusion problems in Banach spaces. J Pur Appl Math. 2019;3(1): 01-04.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

Variational inclusion problems have become the apparatus that is generally used to constrain sundry mathematical equations in other to pguarantee the uniqueness and existence of their solutions. The existence of these solutions was earlier studied and proven for uniform Banach Spaces using accretive operators. In this study, we extend the conditions to hold for arbitrary Banach Spaces using uniform accretive operators.

Keywords

Accretive operators; Banach spaces

In recent years, variational inequalities have been extende in different directions and areas of studies, using novel and innovative techniques. One of such generalization is variational inclusions. Several problems that occur in engineering, optimization and control situations can be modeled by free boundary problems which leads to variational inequality and variational inclusion problems, Eq. 1 in appropriate spaces.

Definition

(Variational Inclusion Problem). Let 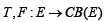be two set-valued mappings, 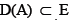an m-accretive mapping, 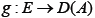a single valued mapping and 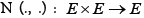a nonlinear mapping. For any given function 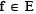and 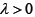, we consider the following problem. Find q 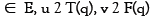such that 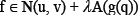(1)

Where E is a real Banach space and E* is its topological dual space. CB (E) is the family of all non-empty convex (closed) and bounded subsets of E.

The duality pairing between E and E*is defined by inner product 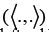if E is a Hilbert space and the Hausdorff metric D (.,.) on CB(E) is defined by

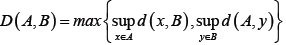
Given that A, B∈CB(E) , the distances d(x,B) or d(A, y) is defined by

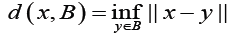(2)

Also, D (T) denotes the domain of T and the normalized duality map is defined by

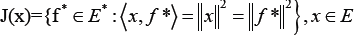(3)

Variational inequalities were introduced in early nineteen sixties by Hartman and Stampachia [1].

Lemma I.1 (Micheal’s Selection Theorem). Let X and Y be two Banach spaces; 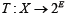a lower semicontinuous mapping with nonempty closed convex values. Then T admits a continuous selection i.e. there exists a continuous mapping 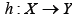such that 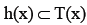for each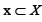

Lemma I.2

Let E be a uniformly smooth Banach space and 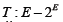be a lower semicontinuous and m-accretive mapping. Then the following conditions hold; (a) T admits a continuous and m-accretive selection

(b) If T is also 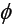strongly accretive, then T admits a continuous m-accretive and 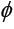strongly accretive selection.

Lemma I.3

Nadler’s Theorem). Let E be a complete metric space, 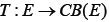be a set-valued mapping then for any given ∈> 0 and for any given 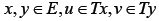, there exists v∈Ty such that

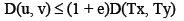(4)

Algorithm I.4

(Iterative Sequence). For any given 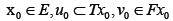compute the sequence 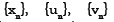by the iterative scheme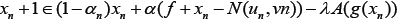

For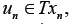

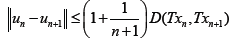
For ,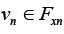

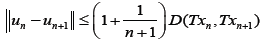(5)

Eq. 5, is called the Mann iterative sequence, it is a direct consequence of invoking Michael’s Selection theorems [2]. Using Nadler’s theorem [3], Chang in [4] proved Lemma I.2, thereby establishing the existence of unique solutions to Variational Inclusion problems using accretive operators in uniform Banach Spaces. In this work we present the extension of Chang’s work to arbitrary Banach Spaces using uniformly accretive operators based on the Lipschitz property of T and F.

Preliminaries

Definition I.2.

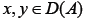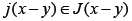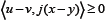Let A be a set-valued mapping with domain D(A) and range R(A) in E. A is said to be accretive if for all there exists such (6)

Definition I.3.

Let 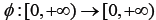be a strictly increasing function with 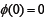then the mapping A is strongly accretive if for an 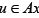, and

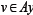
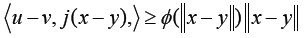(7)

If 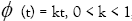then A is said to be k-strongly accretive, and said to be m-accretive if A is accretive and (I + rA)D(A) = E for all r > 0, where I is the identity mapping.

Theorem I.5

Let E be a uniform smooth Banach space, 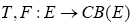and 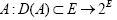be three set-valued mappings, q : E−D(A) a single valued mapping satisfying the following conditions;

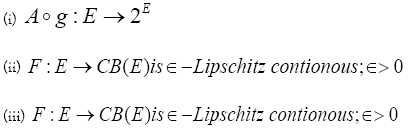
(iv)The mapping 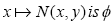strongly accretive with respect to the mapping T, and 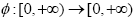is a strictly increasing function with φ (0) = 0

(v) The mapping 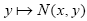is accretive with respect to the mapping F Then, for any given 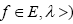, there exists 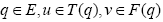which is a solution to Eq. 1.

Theorem I.6

Let E, T, F, A, g, and N be as in Theorem

I.5 and 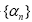, be a sequence in the closed interval [0, 1] satisfying the following conditions

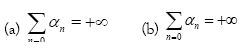
If the ranges 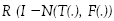and 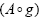are bounded, then for any given 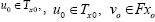, the iterative sequences {xn}, {un} and {vn} defined by Algorithm I.4 converges strongly to the solution q, u, z of the set-valued vibrational inclusion problem of Eq. 1

An equivalent form of Theorem I.6 is given as lemma [5].

Lemma I.7

(Moore and Nnoli). Let {an}, {n} and {n} be real sequences such that 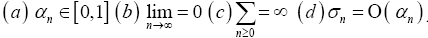Also, let 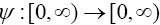be a strictly increasing function with 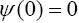if.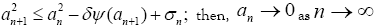

We are not going to reproduce the proofs of these Theorems and Lemmas, it suffices to indicate their implications, conclusions and some of their rudiments as they are used in the course of this paper. For instance, to prove Theorem I.5, one defines the mapping 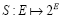that is expressed by 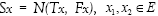and invoke Morales [6] to establish that S is m-accretive and 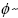strongly accretive and hence use the proof of Lemma I.2(b) to conclude that S admits a continuous and –strongly accretive and m-accretive selection 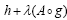. Then, the theorem and proof of Theorem 5.3 in Kobayashi [7] can be used to show that 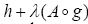is m-accretive and‑-strongly accretive. Then 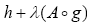can be used to construct a variational inclusion problem that is a subset of Eq. 1 whose solution parses to Eq. 1 by virtue of uniqueness of the element 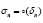. The proof of Theorem I.6 is given in [8] and proof of Lemma I.7 is given in [9]. 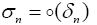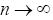The same assumption that, as with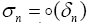 is made in the proof of both (Theorem I.6 and Lemma I.7) in other to establish that the sequences {un} and {vn} are Cauchy in other to achieve the results presented in appendix A. In this study we present a cheaper way to achieve the same result for arbitrary Banach spaces [10].

Results

We begin by presenting and proving the following lemmas, which extends the algebraic property of φ –strongly accretive operators to uniform accretive operators.

LemmaII.1.

Let E be a real Banach space, 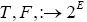two set valued mappings and 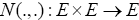a nonlinear mapping satisfying the following conditions;

(i) The mapping 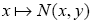is uniformly accretive with respect to the mapping T

(ii) The mapping 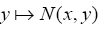is accretive with respect to the mapping F

Then the mapping 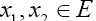defined by Sx=N(Tx, Fy) is uniformly accretive.

Proof: For any given 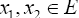and for any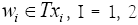; there exists 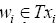and 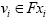such that vi =N (wi, vi). By conditions (i) and (ii) and Definition I.2, we have that

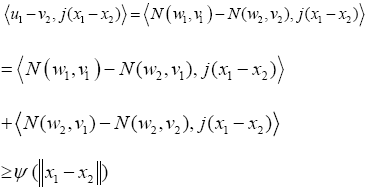
Which implies that the mapping S=N (T(.), F(.)) is uniformly accretive.

Lemma II.2 Let E be a real Banach space and 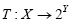be a lower semicontinuous, m-accretive mapping, then the following conditions holds;

(i) T admits a continuous and m-accretive selection

(ii) In addition, if T is also uniformly accretive, then it admits continuous, m-accretive and uniform accretive selections

Proof: The proof of (i) follows from the proofs of

Lemma I.1 and Lemma I.2 (b). For any given 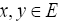and for any 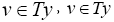, we have from the result of Lemma II.1 that

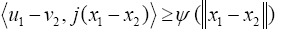
Letting 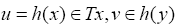we obtain

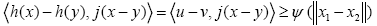which implies that h is uniformly accretive

Now, since T and F are both Lipschitzian, it follows from Eq. 5, that

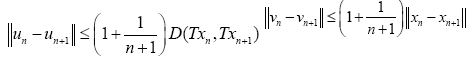
In the same vein,

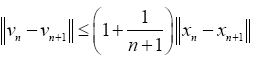
This implies that given any 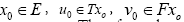the iterative sequences un and vn are cauchy sequences. Therefore, there exists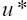, 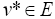such that 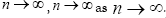By Lemmas II.1 and II.2 and results in results in [5,6,10] we infer that 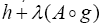too is uniform accretive.

Thus, there exist 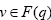and 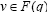such (8) and establish the results 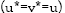in Appendix A with ‘less’ continuity restrictions

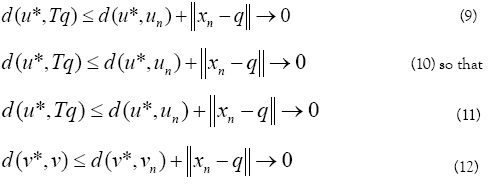
Appendix A

Consequence of Proof of Theorem I.6 and and Lemma I.7

Claim A.1. To prove Theorem I.6 and Lemma I.7, the claim is made that [11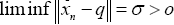-13]

(13)

Proof of Claim:There exists n0 such that for any ,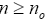

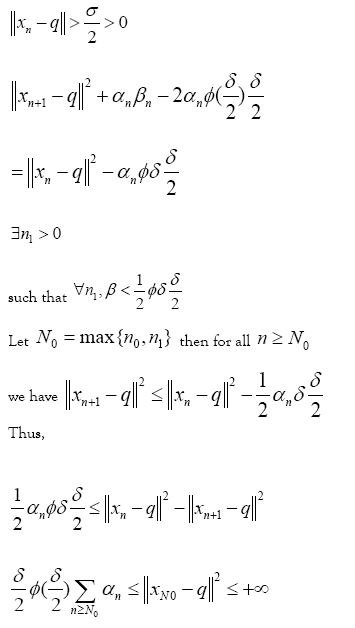
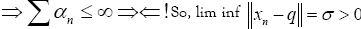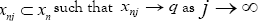
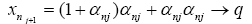and there exists

as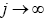. That is, ∀n ≥ 0 Which implies that 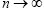as 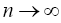Now using the fact that T is µ

Lipschitzian and F is ∈Lipschitzian, it follows that from Eq. 5 that

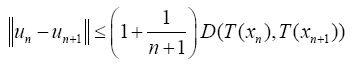
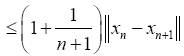
And

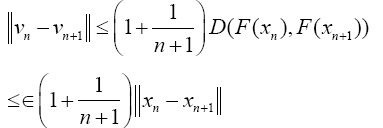
This result implies that the sequences u_n and v_n are Cauchy sequences. Therefore, there exists 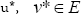such that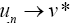 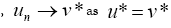. Next, we prove that 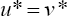In fact, since,

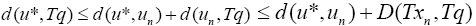
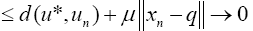(14)

Result of Eq. 14 implies that 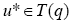Similarly, Eq. 15 also implies that [14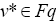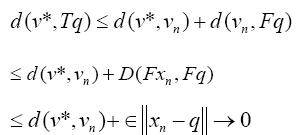,15]

(15)

It remains to show [16] that 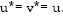But Eq. 16 and 17 clearly shows this.

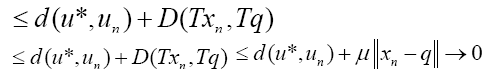(16)

Which implies that 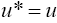and since;

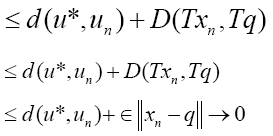(17)

This implies u*= v. [17] Summing up the above argument we conclude that the sequences x_n,u_n and v_n defined by Eq. 5, converges strongly to solution (q, u, v) of problem 1 respectively.

REFERENCES

1. Hartman P, Stampachia G. On some nonlinear elliptic differential-functional equations. Acta Mathematica. 1966; 115:271-310.
2. Michael E. Continuous selections , Annal of Mathematics. 1956; 63: 361-382.
3. Nadler SB. Multi-valued contraction mappings. Pacific Journal of Mathematics. 1969; 30: 475-488.
4. Chang SS. Set-valued variational inclusions in Banac Spaces. Journal of Mathematical Analysis and Applications. 2000; 248: 438-454.
5. Moore C, Nnoli BVC. Iterative solution of nonlinear equations involving set-valued uniformly accretive operators. Computers & Mathematics with Applications. 2001; 42: 131-140
6. Morales CH. Surjectivity theorems for multi-valued mappings of accretive type. Commentationes Mathematicae Universitatis Carolinae. 1985; 26: 397-413.
7. Koboyashi Y. Difference approximation of Cauchy problems for quassi-dissipative operators and generation of nonlinear semigroups. Journal of Mathematical Society Japan. 1975; 27: 640-665.
8. Chang SS. The Mann and Ishikawa Iterative Approximation of solutions to variational inclusions with accretive type mappings. Computers & Mathematics with Applications.1999; 37 :17-24.
9. Chang SS, Cho YJ, Jung JS, et al. Iterative approximations of fixed points and solutions for strongly accretive and strongly pseudo-contractive mappings in Banach Spaces. Journal of Mathematical Analysis and Applications. 1998; 224: 149-165.
10. Martin RH. A global existence theorem for autonomous differential equations in Banach spaces. Proceedings of the American Mathematical Society. 1970; 26: 307-314.
11. Deimling K. Nonlinear Functional Analysis. Springer-veriag, Berlin. 1985; 10-25.
12. Demyanoy VF, Stayroulakis GE, Polyakoya LN, et al. Quassidifferentiability and Nonsmooth Modelling in Mechanics, Engineering and Economics. Kluwer Academic, Dordrecht. 1996.
13. Ding XP. Iterative process with errors of nonlinear equations involving M-accretive operators. Journal of Mathematical Analysis and Applications. 1997; 209:191-201.
14. Hassouni A, Moudafi A. A perturbed algorithm for variational inclusions. Journal of Mathematical Analysis and Applications. 1997; 185:706-712.
15. Noor MA. Generalized set-valued inclusions and insolvent equations. Journal of Mathematical Analysis and Applications. 1998; 228 :206-220.
16. Jung JS, Morales CH. The Mann process for perturbed m-accretive operations in Banach spaces. Nonlinear Analysis.  2001; 43:231-243.
17. Showalter RE. Monotone operators in Banach Spaces and nonlinear partial differential equations. Mathematical Surveys and monographs. 1997 ;49.