Iwuagwus postulations on the behaiour exhibited by the circumscribing center of a triangle, alongside the perpendincular heights

Received: 12-Nov-2023, Manuscript No. puljpam-24-6914; Editor assigned: 15-Nov-2023, Pre QC No. puljpam-24-6914 (PQ); Accepted Date: Jan 29, 2024; Reviewed: 18-Nov-2023 QC No. puljpam-24-6914 (Q); Revised: 21-Nov-2023, Manuscript No. puljpam-24-6914 (R); Published: 31-Jan-2024, DOI: 10.37532/2752-8081.24.8(1).01-02

Citation: Precious IE. Iwuagwus postulations on the behavior exhibited by the circumscribing center of a triangle, alongside the perpendicular heights. J Pure Appl Math. 2024; 8(1):01-02.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

The whole of the postulations made in this paper simply aim at describing the positioning and occurrence of the circumscribing center of a triangle so much so that given any specifications and orientation for a particular triangle, the position could be sketched to exact precision and accurate dimensions without a single construction. With these postulations we are able to to envision clearly and describe where the circumscribing center of a triangle will be located without a single construction detail, all stemming from the fact that by the postulations we are able to study the circumscribing center's behavior with respect to the angles in the triangle given a particular orientation. Contained also in this paper are the mathematical justifications for each postulation made. A rule analogous to the sine rule is also observed but here pertains to the three 'perpendicular heights' obtainable respectively from the three vertices in the triangle, wherein the other two maybe obtained when only one is given alongside all the angles in the triangle.

Key Words

Perpendicular heights; Triangle; Circumscribing center; Dimensions, Position

Introduction

For a clearer depiction let us consider choosing a particular orientation for diagrammatically depicting a triangle. This may otherwise be referred to as the 'conventions' which shall be used to illustrate and prove all the propositions made.

The nine postulations for perfectly locating the circumscribing center of a triangle

The conventions will therefore be to:

1. Take the greatest angle in the triangle to be the 'vertical angle', or 'apex' or the 'top vertex' of the triangle, and

2. To take the side opposite the greatest angle as the base of the triangle.

Sequel to the above chosen conventions we may want to describe a peculiar case of isosceles triangles where the greatest angle in the triangle occurs twice, that is, the two equal angles in the triangle are the greatest angles and the third angle happens to be the smallest we may want to in this discuss refer to such triangles as irregular isosceles, whilst we refer to the other isosceles whose greatest angle occur once and hence the two other equal angles in the triangle become the smallest angles as the regular isosceles .

Having put forth the aforementioned, we may then go ahead to consider the following postulations.

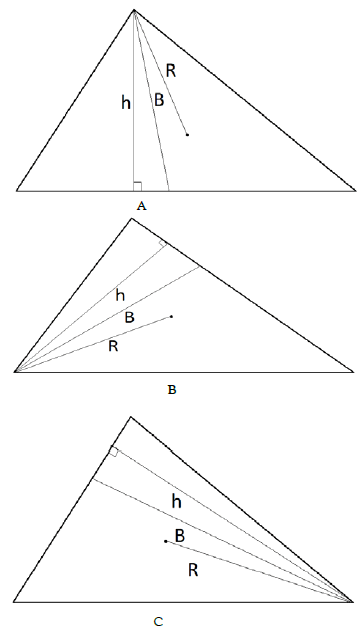
1^st Postulation

There exist for every vertex (angle) in a triangle, three projectable lines namely;

1. A perpendicular height(h) relative to the side directly opposite it (or simply put a height perpendicular to the side directly opposite it)

2. A line of bisection which divides it into 2 equal halves(otherwise called a bisectional height(B))

3. The circumscribing radius of the triangle(R) (Figure 1).

Figure 1: Figure A,B,C for every vertex (angle) in a triangle

2^nd Postulation

For each of the vertices of a triangle, the angle between the perpendicular Height (h) and the circumscribing Radius (R) is equal to the difference between the two other angles in the triangle.

3^rd Postulation

For each of the vertices of a triangle, the Bisectional Height (B) also perfectly bisects the angle between the perpendicular Height (h) and the circumscribing Radius (R). In other words the angle between the perpendicular Height (h) and the bisectional Height (B), is equal to the angle Between circumscribing Radius(R) and the bisectional height.

4^th Postulation

As a consequence of the 2nd and 3rd postulations, it may be observed that, for a vertex, the three projectable lines namely the circumscribing radius, the perpendicular height and the bisectional height may exist explicitly separate from one another provided the difference between the other two angles in the triangle is greater than zero(0). These three lines are however coincident one ontop another whenever the difference between the other two angles in the triangle is equal to 0.

5^th Postulation

For a vertex in a triangle, the circumscribing Radius (R) is given by the following relationship:

R = h ÷ (cosk + cosk_o)

Where:

R = circumscribing radius

h = perpendicular height

K = the difference between the other two angles

k_o = the vertex(angle) being considered

In obedience to the above listed 5 statements a peculiar phenomenon is observed to occur with respect to the greatest angle present in the triangle, hence the following under listed postulations.

6^th Postulation

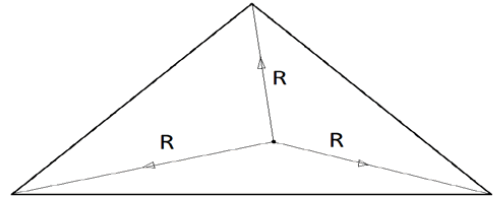
In a triangle where there exists no angle greater than 90, the circumscribing center will always be resident inside of the triangle.

The above statement can simply otherwise be stated thus: When the greatest angle in the triangle is less than 90, the circumscribing center exists above the base of the triangle. (Base here is as defined by the conventions suggested in the beginning) (Figure 2).

Figure 2: Greatest angle in the triangle is less than 90

7^th Postulation

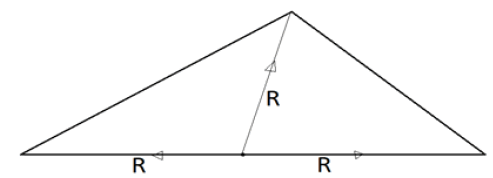
When there exist the angle 90 inside of the triangle, the circumscribing center will occur exactly on the side opposite it.

The above statement can simply otherwise be stated thus:

When the greatest angle in the triangle is equal to 90, the circumscribing center occurs directly on the base of the triangle (Figure 3).

Figure 3: Center occurs directly on the base of the triangle

8^th Postulation

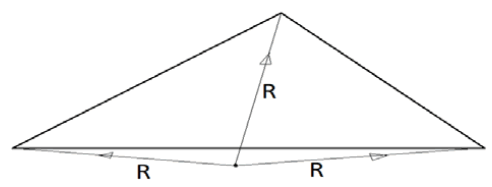
In a triangle where there exists an angle greater than 90, the circumscribing center will always occur outside of the triangle.

The above statement can simply otherwise be stated thus:

When the greatest angle in the triangle is greater than 90, the circumscribing center exists below the base of the triangle (Figure 4).

Figure 4: Center exists below the base of the triangle