Learner self-evaluation on performance rating in Linear Algebra at UPOU with asynchronous methods and synchronous meetings
Received: 13-Sep-2022, Manuscript No. PULJPAM-22-5335; Editor assigned: 16-Sep-2022, Pre QC No. PULJPAM-22-5335 (PQ); Accepted Date: Oct 25, 2022; Reviewed: 30-Sep-2022 QC No. PULJPAM-22-5335 (Q); Revised: 20-Oct-2022, Manuscript No. PULJPAM-22-5335 (R); Published: 30-Nov-2022, DOI: 10.37532/2752-8081.22.6(6).1-7
Citation: Masuhay EP. Learner self-evaluation on performance rating in linear algebra at UPOU with asynchronous methods and synchronous meetings. J Pure Appl Math 2022;6(6): 1-7
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
The purpose of the study showcases the Learner’s self-evaluation on performance rating as part of giving a final grade by uncovering his personal experiences in his education about Linear Algebra at the UPOU. The study adopts and modifies the theory of Rappe & Hayman (1996) on self-evaluation as the basis for rating performance, and used the conceptual framework introduced by Mahmood, Othman & Yusof (2012) in gathering data. Then, Grading Rubrics served as the basis for self-evaluation in giving the final grades by proficiency indicated in the graphics presentation. In lieu of this study asked questions were hypothetically satisfied which revealed that the Learner compared his impressions about the subject prior to and after he took the course; uncovered his difficulties and the causes in linear algebra; emphasized the real significance of the course by enumerating the techniques and skills he acquires which can be helpful on his future career; and described his participation in synchronous meetings with the asynchronous methods, reflected his understanding about the modules, homework, attendance to synchronous meetings, and relating the most helpful aspects about the course; provided self-evaluation on his performance rating from 0 to 100, with 100 being excellent and 60 being average, and justify his self-evaluation performance rating. Thus, based on the Grading rubrics his homework proficiency has accumulated with a total score of 329 over 400 with the equivalent percentage of 82.25% in Homework 1-6 which means within the range from 75%-90% this result contemplated that Learner’s proficiency describes that his homework provides a complete, correct, rigorous proof or solution but is not that written well. Comprises also were outcomes that from monitoring assessment on learning and teaching improvement, it has been recognized by a character that the learner has almost 100% in attendance to the synchronize meetings and participated, communicated in some instance important matters via emails, portal messenger; with complete compliance and perfect submission of homework and obtained a recognizable score by proficiency having 1 item with 60%-80%, 1 item with 90%-99%, and 9 items with 100%, and finally met a maximum rating score of 100% for final (summative) homework. Systematically, based on results from this study, the Learner’s performance rating probably can be computed anytime in the following criterion: Proficiency in Homework+Characteristic in the Learning Process+Monitoring Assessment on learning and teaching improvement+Learner’s Principles in Linear Algebra (rated by the professor) of which the ultimate results for the Learner’s final grade, should be coming from the professor’s personal records and evaluation. Thus, the teacher’s objective criterion for giving a final grade is the ultimate verdict.
Key Words
Self-evaluation on performance rating; Linear Algebra; Asynchronous methods and synchronous meetings
Introduction
As expected by the author Linear Algebra is typically it is about the x, y-axis where demonstrated thru a plot that showcases the fundamental properties of addition and scalar multiplication, with its norms that emphasized the addition and subtraction of vectors. Wherein, students were instructed to comprehend every definition of all related terms, applied the theorems, and provide proofs that reflected the law of addition, associative law of addition, the existence of identity element for addition, the existence of inverse elements for addition, distributive laws of scalar multiplication over addition, associativity of scalar multiplication and identity for scalar multiplication. Then, a manual of examples and solutions is available that contains full solutions for each exercise that guides the learners in their succeeding exercises [1-4].
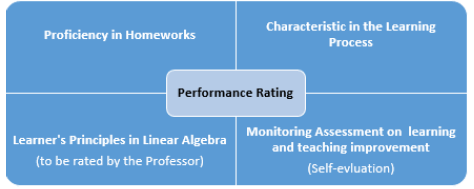
Those scenarios are eventually executed by Dr. Neil Jerome A. Egarguin, Faculty In-Charge in Math211. Linear Algebra this mid-yearterm (MYT), School Year (SY) 2020-21 under Ph.D. Mathematics Education at the University of the Philippines Open University (UPOU), Los Baños, Laguna. Eventually, Dr. Egarguin employed asynchronous teachings that help everyone learn the usage of the Microsoft Team Application whereby all are encouraged for the synchronous meetings within the scope of the whole MYT, SY 2020-21. Technology pedagogy on how to use Mathlab Mathworks and Simulink, Google Drive, emails, and some helpful electronic communication methods are used in this course. This study adopts and modified the theory of Rappe & Hayman (1996) on self-evaluation as the basis for rating performance, and used the conceptual framework introduced by Mahmood, Othman & Yusof (2012), see Figure 1. Self-evaluation in performance rating on Linear Algebra.
In order to satisfy the objectives, and to figure out the learner’s rating performance in Math 211.Linear Algebra, SY 2020-21 in Mid-year term. Such hat to showcase his comparative impressions about the subject prior to and after he took the course; uncover his difficulties in linear algebra and the causes; his findings of the real significance of the course by enumerating the techniques and skills he acquires which can be helpful in his future career; and describe his participation with the asynchronous methods, considering his understanding of the modules, homework, attendance to synchronous meetings, and relating the most helpful aspects about the course; provide self-evaluation on his performance rating from 0 to 100, with 100 being excellent and 60 being average; and justify his self-evaluation performance rating. Thus, this study needs to be realized and so, this intention is beneficial to the educators, students, and researchers for futuristic endeavors.
Methodology
The study
This study is descriptive though it uses some numerical data to give concrete information as pieces of evidence to display the learner’s personal records based on homework scores results, the learner’s promptness in his submission of those assignments thru the submission bin, and his learning improvements were gathered as bases for the Learner’s performance rating self-evaluation but still, the teacher’s evaluation of his learners are given more importance in giving the Learner’s final grade, as it was stressed by Rodin & Rodin (1972) that “there were two ways to judge teaching through the medium of the students: first, the objective criterion of teacher effectiveness is based on what students have learned from the teacher; second, the subjective criterion is based on student evaluation of teacher effectiveness.” [5-6].
The Data
The corpora adopt and modified the theory of Rappe & Hayman (1996) on self-evaluation as the basis for rating performance, and used the conceptual framework introduced by Mahmood, Othman & Yusof (2012) in gathering data.
Data analysis
Schünemann provide suggestions for presenting authors’ conclusions, the methods were used for computing, presenting, and interpreting relative and absolute effects for dichotomous outcome data. However, in this study, we analyzed data from homework scores and applied the Grading Rubrics in Table 1 as the basis for self-evaluation in giving the final grades by proficiency indicated in the graphics presentation [7-8] .
TABLE 1 Grading Rubrics
| Description | % of max points received |
|---|---|
| Provided a complete, correct, rigorous and well written solution or poof | 100 |
| Provided a complete, rigorous and well-written solution though with minor mistakes | 90-99 |
| Provided a complete, correct, rigorous proof or solution but is not that written well | 75-90 |
| Provided an incomplete work that is on the right track or line of thought | 60-80 |
| Provided a complete attempt to the problem but has serious technical errors | 40-60 |
| Submitted a serious and valid attempt to the problem | Oct-40 |
| No submission | 0 |
Then, the author proceeds on the self-evaluation of the Learner’s proficiency by simply using simple mathematical analysis to interpret the logical percentage results of the acquired data from the proficiency in homework as part of the basses in computing the final grade of the learner. The findings, results, and conclusion were presented thru graphical, tabular, and textual expressions.
Findings
Hereby based on the findings results showcase the Learner’s performance in linear algebra in the following aspects: his comparative impressions of the subject prior to and after he took the course; uncovered his difficulties in linear algebra and the causes; his findings of the real significance of the course by enumerating the techniques and skills he acquires which can be helpful in his future career; his participation with the asynchronous methods, his understanding of the modules, homework, attendance to synchronous meetings, and relating the most helpful aspects about the course; his selfevaluation on his performance rating from 0 to 100, with 100 being excellent and 60 being average, and his justification onward to his self-evaluation performance rating.
Learner’s impressions about the subject prior and after he took the course
Linear Algebra is one of the major subjects taught under the Ph.D. Mathematics Education includes field and vector space; bases of vector spaces; linear transformations; matrix representation of linear transformations; and some important algorithms in linear algebra. However, learning has always been difficult since it is highly technical and analytical, but then, this scenario helps to enhance and acquire some new ideas and techniques in teaching especially since the assigned professor is excellent in nature with his pedagogy using asynchronous methods with synchronous meetings. The objective is in giving authentic discussion and assess the learners has been possible easily, his eccentric thought has been replaced with optimistic thinking onward for better results.
Learner’s findings of the real significance of the course by enumerating the techniques and skills he acquires which can be helpful in his future career
Eventually, the Learner learned some significant technology pedagogy on how to use Microsoft Teams Application, MathLab MathWorks and Simulink, and verified that a given set is a field; checked whether a set, together with two operations is a vector space over a given field; proved some statements involving fields; checked whether a subset of a vector space is linearly independent; checked whether a subset space is a basis for the vector space; identify or construct a basis for some specific vector spaces; proved some statements involving linear independence, bases, and the dimension of vector spaces; check whether a given map between two vector spaces is a linear transformation; finds the kernel and range of a linear transformation, illustrate the Rank-nullity Theorem; proved some statements involving linear transformations; find the matrix representation of linear transformation and vice versa; use the matrix representation of a linear transformation of a linear transformation by using its matrix representation; use Matlab to find the rank and nullity of a linear transformation; determined whether a matrix is invertible; calculate various norms of vectors and matrices; proved statements regarding invertible matrices and vector and matrix norms; employ the classical and modified Gram-Schmidt orthogonalization process; finds a QR factorization for a matrix and use this to solve linear system; comment on the conditioning of a matrix; solve linear system the pseudo-inverse of the matrix, and proved statements regarding the aforesaid linear algorithms.
Learner’s difficulties in linear algebra and the causes
His health condition is due to arthritis, the gap in knowledge, unfamiliar to some extent problems, and other intervening factors e.g. prerequisites from other courses enrolled, work-related workloads, and family needs, which resulted in time constraints that made the Learner do his assignments in 24/7 during days and nights just to cope up the deadlines and complied the tasks these factors has caused his difficulties, which sometimes frustrates him to pursue the challenges in this course. But with all the virtues, and God’s blessings he made things possible and succeeded.
The modules provided were highly focused on the technicality and the analytical process which presumed to be that learners are also highly technical hence, it was on the Ph.D. level of studies However, the assigned Faculty is savant genius tried to understand that not all had gone through the process such that learners’ intelligence probably matter on his environment and previous experiences, this exactly the same with the theory [9].
In the teacher’s way to go forward on synchronous meetings he developed the participative approach by having first the survey to find out the plurality of same chosen schedules of meetings, by then, he introduced the asynchronous electronic communication software which is the Microsoft Teams, with his pedagogy the synchronous meetings, was so very interesting and profoundly beneficial to everyone and he even workout on how to guides the learners to be more oriented on using the Microsoft Teams Application.
His expertise in doing lectures would really contemplate satisfy the learners hence, the topics would probably be highly technical and critical it seems difficult for the learner to go forward with what is being explained. However, the learners had been motivated, to attend the scheduled meetings and participated this can be attested because meetings were recorded, although how much the learner wishes to participate more but since topics were still under argument so he only limits his participation but more focused on understanding the lectures provided by his savant professor and so submitted all the prerequisites thereby within his limitations.
Learner’s self-evaluation on his performance rating from 0 to 100, with 100 being excellent and 60 being average, and justify his self-evaluation performance rating.
Ph.D. Mathematics Educations students who enrolled in Math211.Linear Algebra in midyear term, SY 2020-21 has been instructed provided in the course syllabus and modules. Then, in the syllabus, the number of homework problems was enumerated and the deadlines are set, then after the submission of that homework in the submission bin right away it was given with feedback and scores. This how fast and furious on giving feed backing the assigned faculty but with accuracy and complete discussion as to the correction.
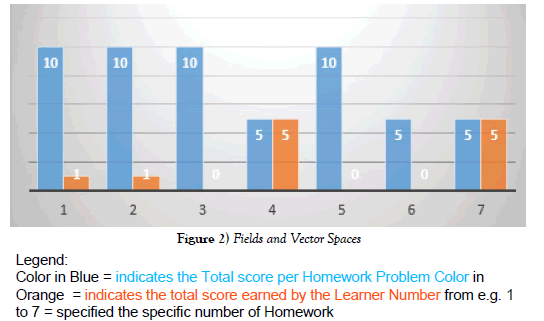
Herewith are the scores earned by the learner and the total number of scores assigned by the teacher were displayed below thru a graphical presentation in sequence from modules 1 to 6, and the score was indicated in detail per homework problem, see below.
Results are shown in a graphical form that the learner has got a minimal score from problems 1 and 2, and also with a perfect score in problems 4 and 7 in Figure 2.
In the actual setting, the teachers give 7 problems but only four should be answered and some of those are flow rated with zero scores. However total submissions of homework problems were mainly done for assurance that he received the answers’ key hence a prerequisite thereby was to submit all the problems prior to the release of the answers key.
But exactly learners were only permitted to do homework at least four (4) out of the seven (7) choices. Below is Figure 2-A. Professor’s Adjusted Homework Problem. So, problems 3, 5, and 6 are excluded from the point system.
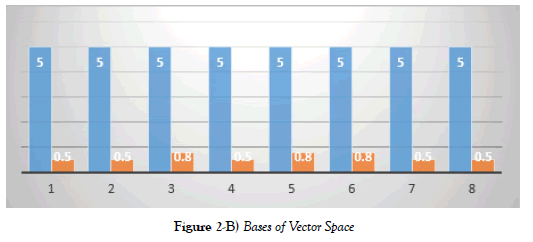
Results are shown in a graphical form that the learner’s scores in proficiency are very minimal ranging only from 0.5 to 0.8 in all of the homework in Figure 2-B. Though this results in rubrics earning an equivalent point ranging from 10% -40% based on the description.
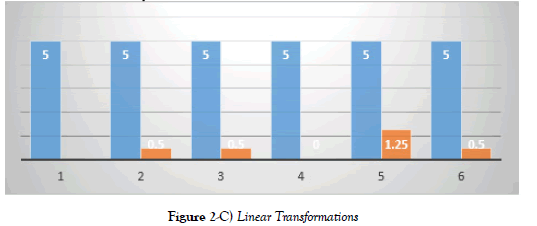
Results are shown in a graphical form that the learner has earned only a minimal score in proficiency out of the six (6) homework in Figure 2-C. Relative only 4 out of the six (6) choices of homework is inclusive for the points system because the learners were advised to choose at least 4 problems out of 6.
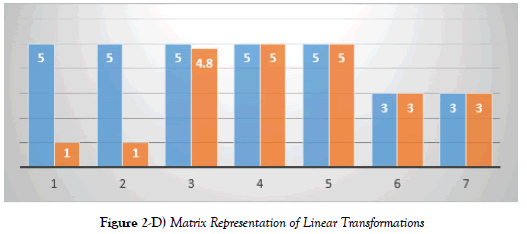
Results are shown in a graphical form that the learner had met the maximum proficiency in five (5) homework out of the seven (7) homework in Figure 2-D.
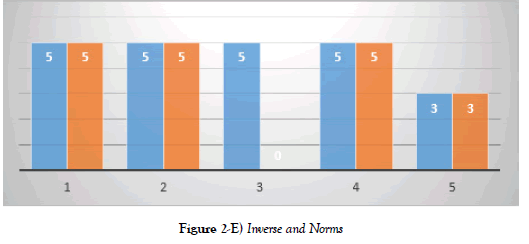
Results are shown in a graphical form that the learner had met a maximum score in proficiency in five (4) homework out of the five (5) homework in Figure 2-E.
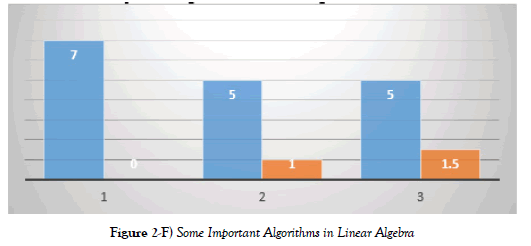
Results are shown in a graphical form that the learner scores in proficiency have got zero in his first problem of the homework then has minimal scores on the second problem and also for the third homework problem ranging only from 1 to 1.25 in all of the homework in Figure 2-F. However, when we focus not on score, progressively the results are optimistic hence, linearly his performance rating was increasing though slowly from zero, next to 0.5, and got 1.25 on the third item.
Homework 7. Final (summative) homework
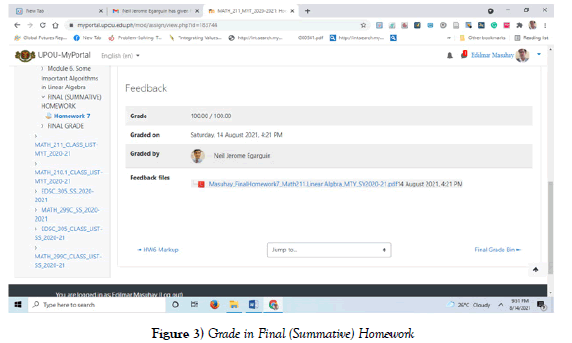
This article will serve as Homework 7, wherein Dr. NEIL JEROME A. EGARGUIN, Faculty In-Charge in Math211.Linear Algebra_MYT_2020-21 in Ph.D. Mathematics Education at UPOU, Los Baños, Laguna gave a final grade based on his objective criterion (see in Figure 3).
The Learner’s Principles in Linear Algebra based on the objective criterion of the teacher has met the highest proficiency with a rating of 100%.
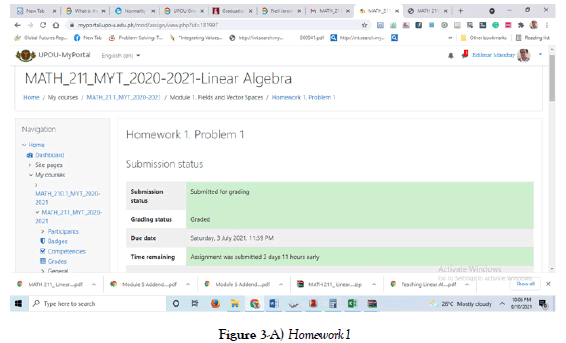
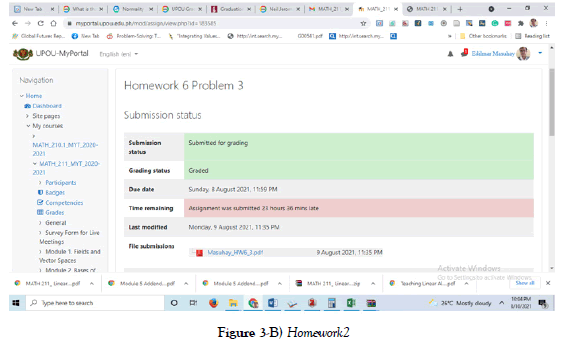
The authors revealed that the learners had completely complied and submitted all the homework from 1-6 on time on the Submission bin, but for practical reasons, only two among the submitted output can be shown thru screenshots Homework 1 and Homework 6 to save the number of article’s pages (see Figure 3-A and Figure 3-B).
Submission of an output has been submitted 3 days, 11 hours early as expected.
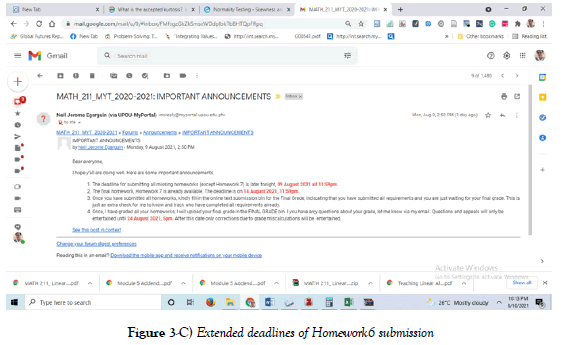
This screenshot declared that submission was late 23 hours and 36 minutes. However, it was proclaimed by the Faculty-In-charge that submission will be extended until August 9, 2011, at 11:59 midnight, instead of August 8 (see Figure3-C screenshot on extended deadlines of Homework 6 submission).
Results and Discussions
Based on records, the learner’s performance rating as to the following aspects, are tabulated on details (see Tables 2, 3).
TABLE 2 Learner’s participation with the asynchronous methods
| Modules No. | Description | No. synchronous meetings | No. of Attendance | No. of Homework Problems | No of Submission |
|---|---|---|---|---|---|
| 1 | Fields and Vector Spaces | 3 meetings in a week | With perfect attendance | 7 | 7 |
| 2 | Bases of Vector Space | 3 meetings in a week | With perfect attendance | 8 | 8 |
| 3 | Linear Transformations | 3 meetings in a week | With perfect attendance | 6 | 6 |
| 4 | Matrix Representation of Linear Transformations | 3 meetings in a week | With perfect attendance | 7 | 7 |
| 5 | Inverse and Norms | 3 meetings in a week | Missed 1 meeting | 5 | 5 |
| 6 | Some Important Algorithms in Linear Algebra | 3 meetings in a week | With perfect attendance | 3 | 3 |
TABLE 3 Proficiency in Homework (as to the grading rubrics)
| Module/Homework | Answered Homework Problem for scoring | Assigned Points Score per Homework Problem | Earned Score per Quiz | % Score per homework problem | % Points earned as to Grading Rubrics |
|---|---|---|---|---|---|
| 1 | 1 | 10 | 1 | 10 | 10-40 % |
| 2 | 10 | 1 | 10 | 10-40 % | |
| 4 | 5 | 5 | 100 | 100% | |
| 7 | 5 | 5 | 100 | 100% | |
| 2 | 1 | 5 | 0.5 | 10 | 10-40 % |
| 3 | 5 | 0.8 | 16 | 10-40 % | |
| 5 | 5 | 0.8 | 16 | 10-40 % | |
| 6 | 5 | 0.8 | 16 | 10-40 % | |
| 3 | 1 | 5 | 0.05 | 10 | 10-40 % |
| 2 | 5 | 0.05 | 10 | 10-40 % | |
| 3 | 5 | 1.5 | 30 | 10-40 % | |
| 5 | 5 | 0.5 | 10 | 10-40 % | |
| 4 | 1 | 5 | 1 | 10 | 10-40 % |
| 2 | 5 | 1 | 10 | 10-40 % | |
| 3 | 5 | 4.8 | 96 | 90-99 % | |
| 4 | 5 | 5 | 100 | 100% | |
| 5 | 5 | 5 | 100 | 100% | |
| Extra 1 | 3 | 3 | 100 | 100% | |
| Extra 2 | 3 | 3 | 100 | 100% | |
| 5 | 1 | 5 | 5 | 100 | 100% |
| 2 | 5 | 5 | 100 | 100% | |
| 3 | 5 | Submission = 0 | 10 | 10-40 % | |
| 4 | 5 | 5 | 100 | 100% | |
| 5 | 3 | 2 | 66.67 | 60-80 % | |
| 6 | 1 | 7 | Submission = 0 | 10 | 10-40 % |
| 2 | 5 | 1 | 20 | 10-40 % | |
| 3 | 5 | 1.25 | 25 | 10-40 % |
Results overviewed that in Module 1 homework, the learner had only gotten a score of 1 on their first and second attempts which adjectively this submission is equivalent to a serious and valid attempt to the problem. But then, the good thing is his homework 4 and 7 have provided a complete, correct, rigorous, and well-written solution or poof in homework. Then in modules 2 and 3 he only got a score on percentages ranging from 10-40% per rubrics scoring system. In module 4 he has a score ranging from 10-40% good for problems 1 and 2, followed by a score ranging from 90-99% for problem 3, and then 100% for problems 4, 5, extra 1, and 2, as well as to Module 5 in problems 1 and 2, yet he missed and got zero in score points but this is good for 10-40% into the assigned rubrics scoring system. Then, got a score of 100% for problem 4, while got only a percentage score ranging from 60-80%. While for Module 6. In some Important Algorithms in Linear Algebra, he only obtains a score ranging from 1-40%.
Moreover, as to the Learner’s Principles in Linear Algebra, he met a maximum score of 100% in the Final (Summative) Homework based on the teacher’s objective criterion.
Characteristic in the learning process
It was being recognized by a character that the learner is attentive in his homework submission, almost 100% attendance to the synchronize meetings and participated, communicated in some instance important matters via emails, portal messenger; with complete compliance and perfect submission of homework and obtained a recognizable score by proficiency having 1 item with 60-80%, 1 item with 90-99% and 9 items with 100%. Besides, gained 100% on his final (summative) homework.
Monitoring assessment on learning and teaching improvement
It was observed that the more exercise and lectures have been provided by the professor the learner got a higher score this is a fact the teaching has been consummated progressively and allows the learner to learn more and acquire new ideas and techniques in solving. Thus, Ph.D. Mathematics Education in UPOU established teaching-learning with experts who could be able to draw conclusive desirable outcomes wherein learners should do things possible in all possible means. However, this strategy in teaching is quite difficult e.g. for those with health problems, and unstable internet connections, these aspects have brought forward the significance of the school management, administrators, or head of offices to be responsive to this call of duty.
Eventually, the teacher’s politeness takeover to make this course admirable and motivates the learner to be more courageous in doing the homework and keep following his advice.
Learner’s principles in linear algebra
The Learner’s principles in Linear Algebra could be observed in this article, the value practically differs from one’s understanding, and this is agreeable that linear algebra has been studied for future careers.
Conclusion
The study has contemplated and satisfied all the hypothetical questions such that the Learner compared his impressions about the subject prior to and after he took the course; uncovered his difficulties and the causes in linear algebra; determined the real significance of the course by enumerating the techniques and skills he acquires which can be helpful in his future career, and described his participation during the asynchronous meetings, reflected his understanding about the modules, homework, attendance to synchronous meetings, and relating the most helpful aspects about the course; provided his self-evaluation on performance rating from 0 to 100, with 100 being excellent and 60 being average; and justified his self-evaluation performance rating.
The author’s self-evaluation has been revealed, the revelation was narrated in the following stanzas, below:
Characteristic in the learning process
Out of the six modules of Linear Algebra that represent a field and vector space; bases of vector spaces; linear transformations; matrix representation of linear transformations; and some important algorithms in linear algebra. The professor has also intended to provide homework within a given set of deadlines, and that by the end of the semester students must be confirmed that he submitted all their homework in the submission bin, and thereby the teacher should grade him a final grade. In this study, the authors within his self-evaluation have partially obtained a passing grade based on the criterion set by the teacher indicated in the Syllabus. Indeed, from the overview of the author, the lectures and discussions have ended fun and progressive. The course is significant for the learner’s professional development and would help anyone’s future career of those who are in the field of Mathematics.
Proficiency in homework
It is also revealed from the Author’s self-evaluation in his performance rating in Math211. Linear Algebra from among the given homework problems he got 16 items with a score ranging from 10%-40%, 1 item ranging from 60%- 80%, 1 item ranging from 90%-99%, and 9 items with a 100% score and percentage. If all the ranges of scores will be flow rated with equal distribution with a numerator score of 100, and favorably the 16 items have got a score ratio of 40:100, then 80:100; 99:100 and 100:100. Therefore, considering the flow the homework has computed with a total score of 329 over 400 based on the rubrics scoring system and has an equivalent percentage of 82.25 which is within the range of 75%-90% which describes that Learner’s homework provides a complete, correct, rigorous proof or solution but is not that written well.
In addition, the Learner met a maximum rate of 100% on his final (summative) homework based on the teacher’s objective criterion.
Monitoring Assessment on learning and teaching improvement
It has been recognized by the character that the learner is attentive in his homework submission, almost 100% attendance to the synchronize meetings and participated, communicated in some instance important matters via emails, portal messenger; with complete compliance and perfect submission of homework and obtained a recognizable score by proficiency having 1 item with 60%-80%, 1 item with 90%-99%, and 9 items with 100% and 100% for the Final (Summative) Homework.
Systematically, based on results in this study the Learner’s performance rating probably can be computed in the following criterion: Proficiency in Homework+Characteristic in the Learning Process+Monitoring Assessment on learning and teaching improvement+Learner’s Principles in Linear Algebra (rated by the professor) of which the ultimate results for the Learner’s final grade, of course, should be coming from the professor’s personal records and evaluation.
Although, the study displayed the fact that the Learner has obtained proficient results in homework, has been courageous in doing and submitting his homework on time, religiously comprehended the modules, attended the synchronous meetings, has learned the technology pedagogy extended through the teacher’s effectiveness but still the teacher’s objective criterion on giving the final grade is the ultimate verdict.
Acknowledgement
All of this success is offered and honored first and foremost to God in the name of Jesus Christ, and second to his parents (Berting and Nena), family (Aiza, Maridel, Eric, Jayrald, Annie, David, Ethel) and to all of his nephews, nieces, and in-laws who with their utmost care at all times.
The author is grateful to Dr. NEIL JEROME A. EGARGUIN for sharing his sincere thoughts, knowledge, and skills which indeed and ended it enhanced the learner’s ability in solving linear algebra problems and for his future career, and realized this article.
It is also his fervent privilege to appreciate the Commission of Higher Education (CHED) at all-time for the scholarship grants during the KTO12 Scholarship Transition Program on his master study at Caraga State University (CSU) and currently for the second scholarship grant under SIKAP for his Ph.D. studies at UPOU.
To his Sending Higher Education Institution (SHEI) the Surigao State College of Technology (SSCT), to the faculty and staff of SSCT for their moral support, especially to Mr. Edwin C. Escobal, Campus Director in Mainit Campus and to Dr. Gregorio Z. Gamboa, SUC President III of their untiring assistance much on their endorsement and approval for his Ph.D. studies, and to SIKAP Scholarship though was not sustaining for a reason.
To his fellow educators and friends: Ludy G. Alsong, Gil M. Alegre, Jerry B. Acero, Rex Bomvet D. Saura, Renz M. Buctuan, and Rustom Padilla, who truly believed in his capacity, and always give their heartfelt encouragement to pursue the study. And to Dr. George G. Posesano on his sincere advises onward to the professional advancement of the author.
The Author
Edilmar Patagan Masuhay is an Assistant Professor-I at Surigao State of Technology (SSCT) presently under the Bachelor of Technology and Livelihood Education (BTLED) Program teaching Mathematics in the Modern World (MMW), and currently enrolled in Math211.Linear Algebra_ MYT_SY2020-21.
References
- Andrilli S, Hecker D.Elementary Linear Algebra. 8:2021;768.
- Rappe M, Hayman K . The effects of video feedback on the self-evaluation of performance in socially anxious subjects. Behav. Res Ther. 1996;34(4):315–22.
- Mahmood A, Othman M F, Yusof Y M. A Conceptual Framework for Mathematical Ability Analysis through the Lens of Cultural Neuroscience. Procedia - Soc Behav Sci. 2012;56:175–82.
- Taylor S E, Neter E, Wayment H A. Self-Evaluation Processes. Pers Soc Psychol Bull. 2016:21(12):1278-87.
- Sedikides C, Strube M J. Self-evaluation: To thine own self be good, to thine own self be sure, to thine own self be true, and to thine own self be better. Adv exp soc psychol. 1997;29:209–69.
- Vallacher R R, Nowak A, Froehlich M, et al. The Dynamics of Self-Evaluation. Personality and Social Psychology Review. 2016;6(4):370-79.
- Rodin M, Rodin B. Student evaluations of teachers. Sci. 1972;177(4055):1164-1166.
- Schünemann H J, Vist G E, Higgins J P, et al. GRADEing Methods Group. Interpret results draw conclus Cochrane handb syst rev interv. 2019;403-431.
- Mackintosh N J. Approaches to the study of animal intelligence. Br J Psychol. 1998;79(4):509-525.