Linear map and spin I. n-focal tensor and Partition function

Received: 13-Feb-2023, Manuscript No. puljmap-23-6157; Editor assigned: 14-Feb-2023, Pre QC No. puljmap-23-6157(PQ); Accepted Date: Feb 28, 2023; Reviewed: 17-Feb-2023 QC No. puljmap-23-6157(Q); Revised: 22-Feb-2023, Manuscript No. puljmap-23-6157(R); Published: 10-Mar-2023, DOI: 10.37532/ puljmap.2023 .6(1); 1-14

Citation: Ziep O. Linear map and spin I. n-focal tensor and Partition function. J Mod Appl Phys. 2023, 6(1):1-14.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

Hyperelliptic theta functions are set in context to ambiguity of using epipolar geometry on twisted cubic curves. Complex multiplication on elliptic curves with ambiguous correlations is set in context to onedimensional complex maps. Chaotic continued fractions are set in context to ternary continued fractions and to the elliptic addition theorem, Poncelet closure and scattering amplitudes in quantum statistics.

Key Words

Continued fractions, addition theorem, Riemann surfaces, elliptic theta functions, twisted cubic

Introduction

Dynamical systems 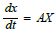are exactly integrable for X dimension X ≦ 4 on genus g ≦ 2 curves E_λ for continuous time 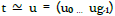where uniformization u and differential d_X describe a Riemann surface X_g of genus g in space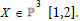

In distinction, det A=0 collinear involutions constitute singular systems. Dynamics of singular systems requires discrete iterated maps 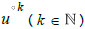with dynamical time k.

Weierstrass Sigma and Zeta functions σ(µ, L) and ζ(u, L) as well theta functions ϑ(u, L ) correspond to quantum states on X₁ or X₂ [3-5].

The present paper approaches quantum statistics on bifurcating, layered X embedded into projective space P³ , projective plane P² and projective line P¹ . Spacetime is set in context to hyperelliptic theta on X₂ where the lattice L is a sum L₀ ⊕ L₁ of tori X₁ [6]. The Weierstrass ℘-function ℘ (u, L) projects from torus T=C/(Z+Zω) for a Lattice L of period ω to foliations of a 2 sphere S² [7].

The Riemann-Hurwitz formula states that a curve of genus ≥ 2 does not admit rational self- maps of degree ≥ 2. A genus on curve in E_λ in P1 with legendre parameter λ is isomorphic to a plane curve E_a with Hesse parameter a. Rational self-maps f of x ∈ P² leave invariant E_a 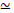E_λ [8]. Iterated x are on the entire sphere S² (Julia set).

Self- maps f of degree deg_x f = 2 are of particular interest. Here a subset γ_H ⊂ f is investigated where γ_H are rational Hermite substitutions as quadratic maps of a cubic polynomial.

Elliptic curves E_λ can be regarded as µ hyperelliptic curves with variable λ [9]. Eλ depends on uniformisers of modular groups, elliptic units, and modular units [10,11]. Period doubling is defined by multiplication of variable z with modular units (3.6) realizing the Kronecker Weber Hilbert Theorem (KWHT) by generating cyclic fields.

The paper proves equivalence between Poncelet closure, addition theorems of elliptic functions and the existence of a 2-power generator μ for involutions and quaternary continued fractions which result from cycles of quadruples k-1, k-2, k-3 and k-4. In the following a cycle describes a cyclotomic field whereas a period describes an elliptic field being two- periodic. In this sense the results of the present paper contribute to KHWT. A period of a continued fraction corresponds to a complex field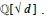

A Continued Fraction (CF) via unimodular collineations 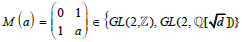is an abelian extension of a rational number field with periods {ā₁} of sequences {a₁ } . One cycle C_M(1) related to a given constant K₁ appears decomposing periods as follows {ā₁} → {ā₁ } {ā₁ } . Ternary continued fractions with unimodular collineations M(a₁, a₂) may exhibit two cycles CM(2) caused by periods {ā₁ } {ā₂ } ā of sequences {a₁ } and {ā₂} {ā₂} are called Bifurcating Continued Fractions (BCF) [12]. Hermite’s problem for describing a cubic irrationality ∂requires a BCF with at least two cycles CM(2). Periods {ā_i } of sequences (a_i ) are equivalent to a fraction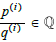

The Weierstrass function ℘µ is invariant with respect to the tent map Tc with c ∈ ℕ or µ₁ of (3.10) [13]. In the simplest case the sequence {ζ} is given by a Cantor string (3.13) which is chaotic. In distinction a relation is drawn between periods of sequences (a_i) and the existence of a constant K_i of a_i power cyclotomic field. Periods {ā_i} of sequences (a_i) are reflected in iterated sequences

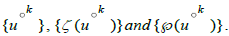
The continued fraction algorithm describes rational solutions via unimodular collineations. Quaternary continued fractions whose unimodular collineations via M(a₁, a₂, a₃) may exhibit three cycles CM(3) caused by periods {ā₁},{ā₂} and {ā₃} of sequences {a₁},{a₂} and {a₃} are called Chaotic Continued Fraction ( CCF ).

The paper relates quaternary continued fraction algorithms for unimodular collineations M (a₁, a₂, a₃) with det M=1 to four SE(3) rigid transformations. Cycles CM(2) and CM(3) allow a highlycomposite (MNT) as a fast decomposition algorithm.

Three points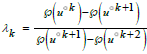 create elliptic units. The addition theorem (4.1) creates four pseudo random points (1,2,3,4) = (pk-1, pk-2, pk-3, pk-4) of a generalized Weierstrass function differing from ℘ by a Hermite transformation γ℘.

At the addition theorem, Poncelet involutions and CCF are isomorph to a SE(3) step. A cycle is equivalent to a cycle of quadruples s=0,1,0’,1’ or k-1 k-2, k-3, k-4 or i = 1,2,3,4 which corresponds to a Frobenius map x → x2

The power tower creates cycles at the third order 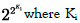is the number of algorithmic steps to catch a cycle {āi} via involutions

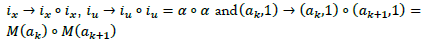
Periods of a 4-polytope formed from iteration steps 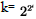are caused by periods {ā} of a cycle {a}, e .g. {11} has period 2. The inner structure of the 4-polytope is inaccessible (or SE(3) kinematics of four steps). Similarly, the inner structure of the surface δXs can be very complicated but four (three) ramification points exist.

At iteration steps 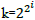(envelopes) a fast algorithm exists analogous to fast multiplication algorithm for large integers. A Discrete Fourier Transform (DFT) is a highly composite Mersenne Number Transform (MNT(k)) of modulus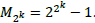

If ∃CM(3) with constants K1, K2, K3 a Signal Processing (SP) includes

• Binary representation for a Power Integral Base (PIB) Z and MNT(K₁)

• a decomposition via the Chinese remainder theorem (CRT(K₂ -1)) with K₂ -1 coprime divisors K of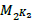

• Fermat Number Transform (FNT (K)) with Fermat number K of modulus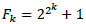

• Mersenne Number Transforms (MNT (K₃)) for highly composite 2- power cyclotomic fields [14].

One of the first algebraic spinor theories is based on hyperelliptic ϑ(u,L) and quaternions q which do not explain bi-spinor representations ψs [5]. Here ϑ(u,L) and quaternions q are embedded in subsequent μs2 foliations with imaginary units 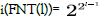which explain four independent complex components ψs.

1. Epipolar geometry and coordinates

A point in space X ∈ P³ imaged by n cameras Cⁱ (i =1,…, n) with x ∈ P² via projections X= Px having 4 rows and 3 columns has matching constraints in computer vision [15]. The joint image Grassmann tensor 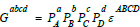forms fundamental, trifocal and quadrifocal tensors for n=2,3,4 cameras having 3ⁿ parameters. Epipolar geometry yields

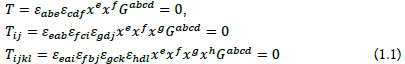
which must hold for each of the 3² and 3⁴ combinations ij and ijkl for n=3 and n=4, respectively. Repeated indices a, b and A, B etc. denoting homogeneous variables in P² and P³, respectively, imply summation. There are only 29 algebraically independent tensor components in total. Calibration of X scenes ∈P³ requires four cameras. An over constrained system T, T_ij, T_ijkl minimizes the vectorization vec G^abcd of the Grassmannian within a linear leastsquares algorithm [15,16]. A point AX depends on 32 parameters e. g. for a complex matrix A. Compared to 29 parameters of the Grassmannian G the question arises whether general X are determinable.

Linear fractional substitutions of x and X yield congruence relations in (1.1) with respect to

and with respect to

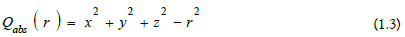
being calibrations in projective space. Thus, rational solutions for space points AX and AX’ are provided with systematic errors ε_focal

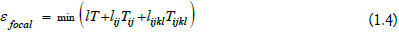
caused by optimizing calibration and currents X-X’.

A metric space calibrated in ℚ satisfies a triangle relation with a Cayley- Menger determinant of rank 3 [17]. A rationalized triangle leads to elliptic and hyperelliptic theta functions [18]. The differential domain with affine connection with torsion having no symmetries on its 43 indices must be separately discussed.

If detA≠0 the substitution X’ =AX is well defined for X ∈ P³ and for 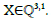Scene reconstruction is possible in computer vision, its complexity is high whereas the information current is low (unique solution).

If det A=0 critical configurations for projective reconstruction with ambiguous correlations X, X ’ , … ,X ∞ appear [19]. Scene reconstruction is not possible, its complexity is low (Gauss fluctuations) whereas the information current is high (∞ solutions). Thus, quantum states and matter with charge and mass are caused by ambiguous correlations of non- unique X with singular A where det A=0.

The error term ε_focal in AX=ε_focal with rational AX is expressed by theta functions. Kummer surfaces K with det K(x) =0 and Weddle surfaces �� with det WX=0 in §16 K(x) and W(X) have matrices linear in x=(x, t=1) and X, respectively [9].

Rational X∈ℚ of elliptic theta functions are iteratively determined via a self- consistent universal covering. u[K λ[gu, L] A one- dimensional uniformization parameter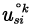 Weierstrass σ- relations 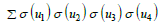depends on iteration index k, parameter i = 1,2,3,4 , index s= 1,2,3,4 of a branched covering δX of a genus 1 Riemann surface with quarter period K of the lattice L ,Legendre parameter λ , modular units g[u,L].

Addition step k, k+1 and k+2 with 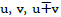can be visualized by a Poncelet polygon in space leading to u, v ε qML with qε ℚ². The idea is to iterate rational maps linear both in 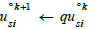where rational q are pseudo- random and would result from undecidable Diophantine equations.

Already a Lattès map as a doubling map 2u← u as an exactly solvable tent map T2 yields fourth order rational quotient functions and a sixth order polynomial . A tent map T_c can be chaotic [7,20-22].

An elliptic curve E_λ over a subfield K of C has complex multiplication (CM) if the ring of endomorphism of 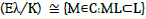≠Z is nontrivial. The multiplier M is understood as a complex constant or a fractional substitution which is not an integer multiple of a matrix in SL(2, Z).

CM of E_λ is singular if M ε ℚ[√d] for an imaginary quadratic field with class number h_d =1 with ed = (3; 2;1) and discriminant d= {-3;-4; - (7,1,19,43,67,163,49)}.

The imaginary quadratic field M ∈ ℚ[√d] describes the normal field ℕ [√d] = K K’ K’’ of a monogenic cubic field K(∂) with irrationality ∂ and its conjugates K’,K’’. For singular CM a lattice L ε K (∂) is homomorphic to an imaginary quadratic field M ∈ ℚ[√d].

Claim 1

One- dimensional interval 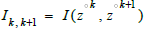and tangent spaces

Tangent spaces or asymptotic lines X ε P³, x ε P² are mapped to onedimensional intervals 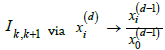with 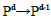homogeneous variables. A map 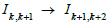of the interval to itself is chaotic if variables zi are on inflection tangents (flex lines) X ε P³, x ε P².

Proof

Let the interval [0,1] = I₀ ∪ I₁. Homogeneous variables X ε P₃, x ε P₂,z ε P₁ of corresponding polynomial equations F(X)=0, F(x)=0 F(z)=0 can be related to each other if Hessian matrices H(F)=0 vanish [23]. A vanishing Hessian H(F)=0 is related to asymptotic lines as lines of zero curvature and singular points and reduces d dimensions to d-1 dimensions. In case of d=1 for a cubic polynomial F(z) one gets an equianharmonic Eλ. Flex lines for binary variables z (asymptotic lines) are defined if three points i, j=1,2, 3 satisfy [24].

where 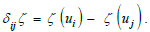Equation (1.5) holds also if the Weierstrass ℘-function ℘(u, L) is replaced by a fractional substitution γ_H ℘(u , L). Condition (1.5) is equivalent that three points z_k , z_k+1 , z_k+2 are on different sites of Eλ flex lines or equivalently, if a simplest cycle exists

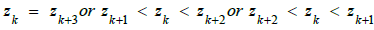for an interval I_k,_k+2. The existence of this simplest cycle yields a chaotic map [25]. Extending the matrix (1.5) denotes the addition theorem (4.1) below ∀k. As a consequence (1.5) is equivalent chaos for 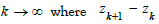is proportional to 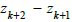giving Feigenbaum constants.

Claim 2 on cycle constants K₁, K₂, K₃

Where a cubic irrationality ∂ where 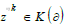requires two generators μ and μ’ of 2- power cyclotomic fields to describe z via BCF with M (a1,a2) [26]. Then z as a two- dimensional DFT of itinerary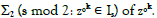

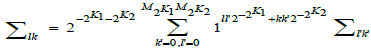
has cycles in the shift map: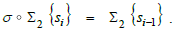

Congruences of cycles CM(n) yield 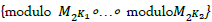for n= 1, 2 , 3. A subsequent map forms a multidimensional MNT with constants K₁,…,K_n.. For K_n ≦8 the map 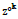is ambiguous.

Proof:

Ambiguous correlations X and X’: AX=0, AX’=0 obey a quadratic map of the interval 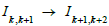where z=℘(u) transforms according to black- box map (2.8) or (2.9). Periods (2.8) of Hermite transformation 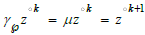and 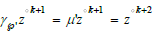are roots of the characteristic equation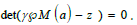

The z- degree of 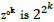three congruences CM(3) in a CCF matrix M(a₁, a₂, a₃) in (3.2) can be approximated as a direct product by abelian extensions of the rational number field. However,

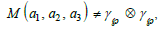
BCF and CCF in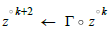 require a crossing term in the black box operator Γ with at least two CF periods. As a result Hermite’s problem for ∂ is ambiguous. However 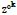is highly

composite and allows a CRT(K₁- 1) decomposition of 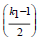pairwise coprime divisors and a fast FNT(K₁) followed by a fast MNT(K₂) in the limit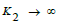

Whereas a multiplication of polynomials f requires deg2f steps a fast 2- radix DFT requires deg f log deg f steps.

Cycles imply the existence of elliptic units g(q_sω, L ) (3.6) with 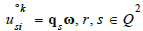as units of the modular group 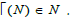Maps γ_℘ are as well quadratic and linear substitutions of cubic roots leaving (3.8) invariant. The Legendre module λ of E_λ depends on uniformisers of the modular group (N) enveloping (3.6) [10].

Weierstrass relations 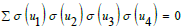are invariant if four parameters suffer substitutions 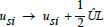with a matrix Û of two columns and four rows having 28 values 0 or 1[27].

Two iterates 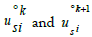differ by two ½ ÛL values.k iterations differ by 2^k values ½ ÛL which yields congruences, i.e. maps are ambiguous for CM(i) if Ki ≦ 8. Substitution matrix

Û _k→k+1 u have rank four. The itinerary 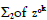is defined by Σ₂ {s 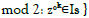[22] .

The shift map σ is defin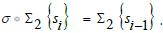ed by A DFT of a is defined by

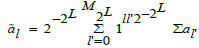
as a congruence module 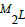Two congruence moduls 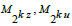yield 2D DFT,

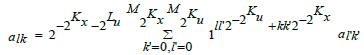
Power-2 cyclotomic fields allow a fast decomposition of 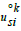in terms of congruence modules with Fermat number F_t via K₁ =8 in

A peculiarity is that 2-power towers of bases 3 and 2 are generators mod F_t. Number 2 and 3 are primitive roots of unity of FNT (t) for t≦4 which do not split within 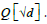Roots of unity correspond to ray class fields of lattices L establishing a connection between μ and μ’ and modular units 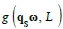in (3.6). 2- power cycles create the simplest cycle 1^⅓ [25].

A Lattès map 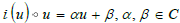is understood in terms of CM fields, i. e. 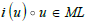. In distinction i(u) is identified with a Poncelet involution i²(u) = 1.

A chaotic map exhibits 2^k periodic cycles: ∃C_M(3). Pseudo- random number 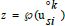of one-dimensional map γH are exactly solvable maps of Eλ within interval [0,1] [13]. CM transfers the endomorphism for a complex constant 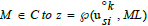implying existence of PIB [11, 28]. A PIB regularly maps I→ I’ of exactly solvable chaos.

A sum 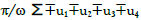corresponds to spherical triangles of S² [29]. The coefficient π/ω is irrational and depends on a ternary blackbox map for 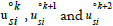as follows

with a black- box matrix 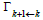of four columns and four rows.

An arithmetic-geometric mean algorithm of Gauss (agM) 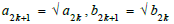BCF (Jacobi algorithm) with 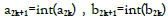depends on three or four columns. The agM limit 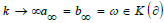yields the Dedekind eta function η(ω) and Weber- Schlaefli invariants f (ω), f₁(ω) as

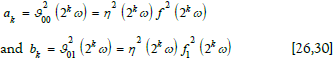
In dependence on initial a₀, b₀ values a limit is reached 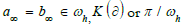where ω_e or ω_h are equianharmonic or harmonic (lemniscate) constants. A ternary BCF limit for 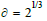yields period 2 sequences a = { 1 (1 2) } and b = { (1 0) }. A ratio 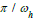calibrates 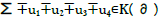between T and S² where Σ 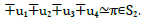The calculation π/ωh requires a 4- component algorithm (1.7) in case of harmonic E_λ and ω_h. An infinite expansion in (1.7) goes over 2-power maps of f(ω) which can be approximated by cyclotomic units μ.

Below this μ- expansion is confirmed by a hyperelliptic doubling map which relates spinor states to iterations of Weber- Schlaefli invariants f(ω).

According to (4.1) this expansion holds also for u,ζ(u) and��(u) ε K( ∂) [31]. For a fractional substitutio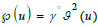 , one gets also 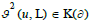[31].

Claim 3: Cyclotomic units and Riemann surfaces δX

Cyclotomic unit’s μ and μ’ couple hyperelliptic surfaces on layers

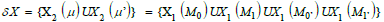
as elliptic curves E_λ and E_λ’ with variable Legendre module λ and λ’, CM multiplier Ms, and uniformization parameter us where s=0, 1, 0’, 1’.

Proof: Rational self- maps of the T = X1 to itself are constrained by the Hurwitz automorphism theorem [32].

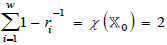
with Euler- Poincaré characteristic χ. The number of branch points w is identical to the number of generators as ri th roots of unity in δX. The branched covering δX are four layers as tori with four branch points {ri}={2,2,2,2} or three branch points {ri}={2,3,6} , {2,4,4} or {3,3,3} [33,7].

Conclusion

The elliptic addition theorem has a pseudo-random component used in cryptography. Here a pseudo-periodic component is investigated as a recurrent random walk in one and two dimensions.

C_M(1) cycles of u, ζ, ℘ on universal covering δX are related to SE(1) dynamics. The partition function (3.20) is in relation to coordinates and Euclidean number. Cycles C_M(2) have a longitudinal and a transverse component and are called bosons. Cycles C_M(3) have a longitudinal, transverse and rotatory component and are called spinor fields.

Processes (1.8), (1.11) and (4.13) describe an SP information current I whose equilibrium state is a sum of positive and negative rational values with I=0 ε Z. Fermions are bilinear idempotent n_l with congruences a, ā in C_M(3).

Generators μ, μ are roots of unity as one dimensional representations of the rotation group where is a direct product.

Binary invariants arise from Aronhold processes which are invariant with respect to fractional substitutions γ ε SL( 2, Z). δi is non-symbolic if a_i, b_i ε Q

A bilinear representation ℘ , ϑ or σ is a fast 2-power decomposition modulo and

As a result the Bethe- Salpeter equation (4.13) and Feynman diagrams obey a CM endomorphism for discriminant (4.9) with

Summation in (4.10) and (4.11) is over theta function characteristics (4.3) of one dimensional complex maps of ϑ(u) having cycles with an one-dimensional wave vector. The relevant function on sheets s = 0,1,0’,1’ of δX projects according to (1.20) from torus T to sphere S². The product of hyperelliptic σ(u) σ(u’) as a product of four elliptic theta (4.3) on δX leads to a 4 dimensional generator exp(ik_i x_i) with k_i x_i ( i=1,2,3,4) which corresponds to microstates where

Bloch states arrange themselves as reducible g=3 theta functions leading to hyperelliptic Weierstrass functions

Minkowski spacetime (x, ct) ε Q^3,1 with rational x , complex parameter c and complex continuous time is realized in the limit k →∞ where k ε C gets complex.

The addition theorem (4.1) for u, ζ and ℘ depends on bilinear compositions (4.11). The determinant (4.1) vanishes if and undergo unimodular collineations.

Due to the N th iterative of (4.1) yields a N th order determinant in terms of log g(q_sω,L) where q_s=(r, s)εQ² which is equivalent with the regulator R of the system of modular units (3.6) with ML. For modular groups Γ(N) the regulator R is given by a circulant matrix of elliptic units. The Slater determinant implies the presence of a power tower of generators g(u,L) as a product of sigma functions is equivalent to the regulator R of units in Q [√d] K [∂].

The square root √Δ is a limit of an expansion of quantum statistical scattering processes in terms of cyclotomic approximations of vertices Γ and states ψ.

Appendix 1 Poncelet theorem for quadrics in space

The Poncelet theorem for quadrics in P² and P³ and the addition theorem for elliptic functions (4.1) are equivalent. As a result indices s=0, 1, 0’, 1’ correspond to a quadruple k-1, k-2, k-3, k-4 in (3.3) on δX. The involution matrix αss’ depends on parameters a_k, b_k and c_k in (3.3) algebraically.

Rational quadrics (1.9) map θ ε P¹ to a point on the twisted cubic C_tw. A Weddle surface W(X) =Σx_iQ_i(X) as a pencil of 4 quadrics Qi(X) ε P³ is projected onto δX as 6 pencil of 2 quadrics Qi(X) ε ℙ³. A pencil of two quadrics Qi(X) ε P³ splits into four conics in ℙ². The Poncelet closure theorem states that infinity of rational solutions exists if a closed n- polygon in P² and a 4 polytope in P³ is formed. A partial line (P, T) of a closed 4-polytope of dimension s=0, 1, 0’, 1’ consists of points P and tangents satisfying (4.1). The closure condition is a periodic pair of involutions i_x(P,T) and i_x’(P,T)

The closure condition is an identity map on δX

The branched covering δX consists of sheets s=0, 1 and s=0’, 1’. Functions u, ζ and ℘ in addition theorem (4.1) with index quadruple (0 ,1 ,2 ,3 )= (0, k, k+1, k+2 ) on δX yield triples which arrange K=2 groups with κ=1,2.

Two involutions ix and iu yield four matrices α(κ), α(K +κ) which form a group G₃₂ of order 32. The elements of G₃₂ are

On a definite sheet of a quadruple {0, k, k+1, k+2} one has α = -1 ε R. A closure of the 4-polytope takes place if

leading to u= q_sωεML (r,s)εQ² which emphasizes that the Poncelet theorem and the addition theorem are closely related to modular units.

Each iteration k generates a Kronecker product A(M, u, ζ, ℘)→A(M, u, ζ, ℘) A(M, u, ζ, ℘) of matrix A(M, u, ζ, ℘) in (4.1) and of involution matrices αα → α.

Subsequent k generate imaginary units i(FNT(k)) via CRT, MNT and FNT decompositions and a complexification. The relevant group of order 32 for complex a, a⁺ consists of Gamma matrices and Dirac matrices Γ_μ . Individually u, ζ and ℘ reflect the symmetries of G₃₂. As shown in §18 and §44 of 32 places x, X of det K(x)=0 , det W(X)=0 and 32 tangents (2.3) constitute group of the order 32.

Appendix 2 Transition from robot dynamics to chaotic dynamics

CF, BCF and CCF matrices M(a), M(a₁, a₂) and M(a₁, a₂, a₃) with n=1,2,3 in (3.5) and (3.2) are given by

with a cyclic matrix of order zero matrix with n rows and m columns. One has

which contains one and two- dimensional collineations if {a_i=0 ∧ a_j=0} or {a_i=0} ∀i, j=(1,2,3). Even for chaotic collineations invariances exist. Firstly (1.5) is invariant with respect to Hermite transformations (2.4). Secondly a nilpotent N₀ exists for ∀M(a) which can be written as in terms of Dirac matrices Γμ. The idempotents are related to projection operators for four- component bases.

Variables x= (x, 1) transform under action of the special Euclidian group SE(n) for n- cycles shifted

For different rotation matrices Rk one has

Then M(a) corresponds to a quadruple of imaginary rotations R_k for position vector and ambiguous rotations R_k. The CCF matrix allows a fast with R a rotation matrix with R₄=1

The equation for the matrix S yields the following idempotent P₀, P₊, P- and the nilpotent N₀

as 4x4 matrices which are independent on a definite vector x. In dependence on P₀, P₊, P- and the nilpotent N₀ the matrix S reads