Logical necessity of Quantum Mechanics

Received: 11-May-2023, Manuscript No. puljmap-23-6421; Editor assigned: 13-May-2023, Pre QC No. puljmap-23-6421(PQ); Accepted Date: May 25, 2023; Reviewed: 16-May-2023 QC No. puljmap-23-6421(Q); Revised: 19-May-2023, Manuscript No. puljmap-23-6421(R); Published: 15-Jun-2023, DOI: 10.37532.2023.6.2.1-2

Citation: Cadeddu EPG. Logical necessity of quantum mechanics. J Mod Appl Phys. 2023, 6(2):1-4.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

From classical mechanics, in particular the motion in a straight line, together set theory and ordinal number theory we prove a not classical behaviour, a discontinuous motion and emission.

Key Words

Quantum; Ordinal numbers; First transfinite ordinal number; Uncertainty principle; Zeno discontinuous; Motion successor

Introduction

Quantum mechanics axioms imply the not-classical behaviour;mathematically, from Hilbert space and linear operators, it is deduced that only discrete spectrum of eigenvalues has a physical meaning. They are justified by specific physical observations such as the well-known black body radiation and wave behaviour of matter, in contrast with classical physics [1].

Zeno, with his paradoxes, stated the impossibility to reach all infinite parts of a segment, but not in a clear way, getting at the conclusion about the impossibility of motion.

We define more precisely the problem and with the help of the concept of the first transfinite ordinal number ω(see Cantor) we get the existence of discontinuous motion and emission, instead of stating the impossibility of motion [2,3].

Discontinuous motion and emission

Suppose to divide a finite segment into infinite N parts dx that is 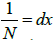is an infinitesimal part, with N an infinite hypernatural number. This correspond to a continuous x (space) eigenvalues spectrum.

Imagine a partdelimited by two points. We observe an object going from the first point to the second, third, fourth and so on. But it is not possible to observe the object crossing all infinite points. Inductively it is not possible to reach infinity from the finite, as follows.

With a proof by induction the well-known fact that each natural number is finite can be shown. Induction step is proved using the Dedekind definition of infinity and finite [4].

So if n is finite, then n + 1 is finite; because n + 1 doesn’t have an infinite subset.

Then the first transfinite ordinal number ω is not a successor of a natural number (the successor of a natural number is a natural number, a finite number), that is so, starting from the finite, one by one, the object doesn’t reach all infinite points.

But the object runs across the entire finite segment in a finite time!

But the object runs across the entire finite segment in a finite time! So the object has necessarily to cross a finite number of points and the motion of the object along the segment is discontinuous. This consideration is in concordance with Schrodinger equation, just think of a particle in a box; considering knots and maximums of probability it doesn’t have a continuous motion.

The same consideration is valid along a finite time interval. So a flow of energy or matter is observed discontinuous; it is not possible to count an “infinite number” of infinitesimal portions of energy or matter to go out a surface. In this way corpuscular theory of light and matter rises, in a qualitative manner.

But how many finite parts are there and, above all, how small is a part?

They may be so small to become infinitesimally; there is no limit in reducing a single part, except the previous consideration about finite number of points in a segment. It is necessary a law to avoid a contradiction (Δx cannot be infinitesimally and Δx can be infinitesimally).

A solution is the Heisenberg uncertainty principle, in particular 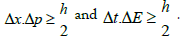So Δx = dx and Δx = dt only when Δp = ∞ and ΔE = ∞ but, at these conditions, p and E are not observable, being 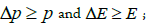we cannot describe the motion of an objectand then wedon ’ t observe a continuous motion.

Conclusion

Zeno didn’t define rigorously why it is not possible to reach all infinite parts of a segment, and over the centuries efforts were focused on proving reachability of infinite totalities, utilising series and integrals. It was believed that the paradoxes were solved, without to consider them in the general context (the entire path and motion).

Now we have obtained that the not-classical behaviour is essentially due to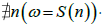

But incredibly this could have been discovered about 140 years ago, before Planck theory. So quantum behaviour looks very natural and classical mechanics has to be rejected. The classical limit h = 0 cannot exist.

References

1. Battaglia F. Classical and quantum physics lessons. CEDAM 1996.

   [Googlescholar]

2. Cantor G. Foundations of a general theory of manifolds, Collected treatises on mathematical and philosophical content . 1932

   [Googlescholar]

3. Guthrie WK, Guthrie WK. A History of Greek Philosophy,  The Presocratic Tradition from Parmenides to Democritus. Cambridge University Press; 1962.

   [Googlescholar]

4. Joyce DE. Notes on Richard Dedekind's what are numbers and what are they supposed to do. Preprint. 2005

   [Googlescholar]