Magnetic and hydrogen storage properties under the action of a sinusoidal electromagnetic field by the LaNi3.6Al0.4Co0.7Mn0.3 alloy
2 Department of physics, College of Science-Qassim University, Al molaydah Buraydah: 51452-P.O.Box: 6644, Saudi Arabia
Received: 11-Jun-2023, Manuscript No. puljpam-23-6524; Editor assigned: 15-Jun-2023, Pre QC No. puljpam-23-6524 (PQ); Accepted Date: Jul 09, 2023; Reviewed: 20-Jun-2023 QC No. puljpam-23-6524 (Q); Revised: 05-Jul-2023, Manuscript No. puljpam-23-6524 (R); Published: 31-Jul-2023, DOI: 10.37532/2752-8081.23.7(4).219-224.
Citation: Belkhiria S, Chaker B, Dhaou MH, et al. Magnetic and hydrogen storage properties under the action of a sinusoidal electromagnetic field by the LaNi3.6Al0.4Co0.7Mn0.3 alloy. J Pure Appl Math. 2023; 7(4):219-224.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
The detection of the response of an intermetallic compound to a magnetic field consists of a precession on the spin displacement and the associated damping. The displacement of the magnetic spin results in a change in the crystallographic structure and subsequently a change in the properties of hydrogen storage. Thus, in order to improve the performance of hydrogen storage within the LaNi3.6Al0.4Co0.7Mn0.3 intermetallic, and aware of their significant effect on the storage of hydrogen, we propose firstly, to consider an experimental study of the magnetic properties of the LaNi3.6Al0.4Co0.7Mn0.3 intermetallic compound. For this, a sensitive Vibration Sample Magnetometer (VSM) is used. Then, the mass of hydrogen absorbed / desorbed under the effect of a sinusoidal electromagnetic excitation has been presented.
Key Words
Magnetic hysteresis cycle; Virgin magnetization curve; Rayleigh calculation; Electromagnetic field; Hydrogen absorption; Hydrogen desorption
Introduction
The depletion of fossil fuels and the growing demand for energy have led researchers to develop new energy storage techniques. Among which, the storage of hydrogen in the form of metal hydrides in Metal-Hydrogen Reactors is recommended. The LaNi5 intermetallic and its derivatives are very attractive for the reversible storage of hydrogen since they are able to store hydrogen in moderate temperatures and pressures which gives them the safety advantage [1-10]. The study of the hydrogen storage properties in the LaNi5 intermetallic and its derivatives remains the interest of several experimental and numerical recent researches [11-14]. To improve the reversible hydrogen storage properties in the LaNi5 compound, researchers focused on the one hand on the study of the key operating and design parameters: initial experimental conditions, reactor configuration, heat exchanger [15-17]. In the recent years, the coupling of the hydrogen metal reactor with a Phase Change Material (PCM has been widely studied [18–20]. The found results showed that when the PCM is used the hydrogen storage process is faster and the reaction kinetics is improved. The effect of the incorporation of the natural graphite on the compacts LaNi5 hydrogen storage properties. The results showed that the heat transfer within the hydride bed and the hydrogen storage capacity are improved and the time reaction is reduced [21].
On the other hand, several researchers focused on the study of the effect of the controlled substitution on the enhancement of the reversible hydrogen storage by the LaNi5 [22-26]. The effect of Sn on the stability of the LaNi5-xSnx (0<x<0.5) was studied [27]. They observed high stability of the sample, which contains the element Sn. On the other hand, the absorption time is not strongly influenced by the addition of Sn, but desorption is delayed when the content of Sn is greater than 0.4. A comparative study of the storage properties of the LaNi5 compound and the LaNi5-xSnx compound showed that the parent compound has the higher hydrogen storage capacity [28]. The effect of Co doping on Ni sites on storage isotherms has been studied [29]. Results showed that the Co addition partially combines the phase β and γ and contributing to a higher cycle stability during long-term cycling. The substitution of Ni by Al and Co to combine their effects has been considered [30]. The results showed that the addition of Co renders the intermetallic resistant to decrepitation, while the addition of Al decreases the dislocation rate. The compound LaNi3.95Co0.75Al0.25 combines the two effects. The combination between Co, Mn and Al has also been considered in the study of the hydrogen storage properties by the LaNi3.6Al0.4Co0.7Mn0.3 compound [31-33]. The results showed that the hydrogen storage reaction is improved marked by an enlargement of the interstitial sites and the isotherms equilibrium plateau is lowered.
In this paper we propose in the first part, a study of the physical properties (structural and magnetic) at room temperature of the LaNi3.6Al0.4Co0.7Mn0.3 compound. In the second part the hydrogen absorption and desorption reactions by the LaNi3.6Al0.4Co0.7Mn0.3 compound under the action of a sinusoidal variable electromagnetic field as a function of initial temperature are studied. In previous published works, we have studied the hydrogen desorption by the LaNi5 compound under the action of an electromagnetic field and reversible hydrogen storage under the action of a magnetostatic field [34-35]. To our knowledge, the proposed work has not been done by considering these experimental conditions and the same doped compound.
Experimental Steps
Structural characterization
The X-ray technique is used to identify the crystalline phases present in the doped intermetallic compound and to determine its structural parameters. For this, an X’Pert diffractometer is used which uses a θ-θ arrangement in Bragg-Brentano geometry. All measurements are made by a copper anticathode. The acquisition of the diffracto-gram data is done in a step of 0.04.
Magnetic measurement
The intermetallic compound was prepared from the high-purity elements (99.9%), in a sample holder is made in a glove box, under an argon atmosphere to avoid any surface passivation of the material with other gas. It was mechanically crushed out using a ball mill until obtaining particle sizes around 50 μm.
A Vibrating Sample Magnetometer (VSM) is used. The principle of measurement is the following: The sample is placed into a uniform magnetic field (H) where it acquires a magnetization M. It is moved inside coils. The magnetic flux passing through these coils is disturbed. In a superconductive loop, the flux must remain constant and quantified: an electric current is then induced in the circuit. This current creates a local flux variation in the coupling coil. This variation induces an alternating current in the SQUID. The output voltage of the amplifier is proportional to the variation in the number of initial flux quantum. The sample is moved in successive steps, each measurement of the flow variation form a point on the extraction curve. This curve is filtered to obtain the value of the magnetization.
Hydrogen storage measurement
The experimental devices as well as the hydrogen storage steps have been described in our previous published works [34-35]. 30 g of the intermetallic was prepared and placed into a copper reactor. The reactor is surrounded by a coil powered by a variable voltage generator (f = 50 Hz) and it is connected to a hydrogen tank by connecting tubes. A pressure sensor is installed between the reactor and the hydrogen tank to control the pressure variation during the reaction. The voltage delivered by the generator has been adjusted so as to reduce the effect of the electromagnetic induction heating. This is done by minimizing the energy dissipated by Joule effect. Thus, the reactor was crossed by a voltage of 0.9 volt. This voltage does not produce electromagnetic induction heating which allows us to focus only on the effect of the electromagnetic excitation on the hydrogen storage reaction by the intermetallic. An oscilloscope and a digital multi-meter were used to control the voltage delivered by the generator during the experiment. The reactor is immersed in a cylindrical aluminum heat exchanger which guarantees the cooling and heating of the hydride bed during absorption and desorption reactions by heat transfer water coming from the thermostatic bath. The water circulation in the heat exchanger is via a water inlet/outlet in Figure 1.
Results and Discussion
XRD analysis and Ritveld refinement
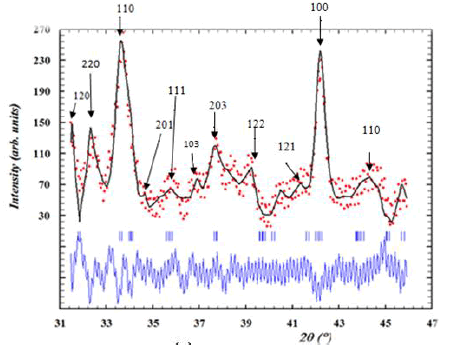
X-ray diffraction patterns of the LaNi3,6Al0.4 Mn0, 3 Co0,7 intermetalliccompounds is shown in Figure 2. The Rietveld refinement allows usto have a clear idea on the structure, the space group and theparameters of the parent and the doped intermetallic compounds(Table1). It is shown that the compound is a single phase with anorthorhombic crystal structure. The LaNi3,6Al0.4 Mn0, 3 Co0,7 crystallizesin a Pnma space group.
Table 1 presents the values of the crystallographic axes and the unit cell volumes obtained from the XRD data.
TABLE 1 Results of the Rietveld refinement
| Space group | a (Å) | b (Å) | c (Å) | α | β | δ | Chi 2 |
| Pnma | 74,57,698 | 74,61,279 | 85,66,137 | 90° | 90° | 90° | 3,49 |
Magnetic properties
Hysteresis cycle
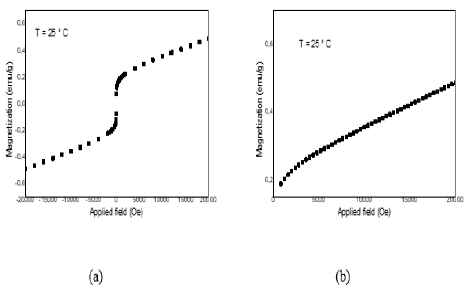
Figure 3a represents the magnetic hysteresis cycle intermetallic compound at 25°C. It illustrates the relationship between the magnetization of the material and the applied magnetic field. The curve has three distinct zones:
• First zone: it is a linear zone. In fact, when the field increases the magnetization increases also. However, the increase due to magnetization is very slow compared to the increase in the field.
• Second zone: This zone is characterized by a remarkablevariation of the magnetization against zero fields.
• Third zone: it is a linear zone which shows that parentcompound reached saturation, however for the dopedmaterial it is not reached at the tested conditions.
Results found in Table 2 showed that intermetallic is magnetically soft presenting weak coercive field Hc (field at which M=f(H) change sign) and weak ramanant magnetization Mr (M at H=0). It has a paramagnetic character marked by a positive magnetic susceptibility χ.
TABLE 2 Experimental magnetic parameters from hysteresis cycles
| Hysteresis parameters | Up | Down | Average | Definition |
|---|---|---|---|---|
| HC(Oe) | 38.486 | -38.637 | 38.561 | Coercitive field at which M/H changes sign |
| Mr(emu/g) | 7.47E-02 | -7.49E-02 | 7.48E-02 | Ramanent magnetization: M at H =0 |
| S | 0.144 | 0.136 | 0.14 | Squareness Mr/Ms |
| Permiability | 2.11E-06 | NaN | NaN | Permiability calculated from slope H2H3 in SI (H/m) |
| Ms(emu/g) | 517.420 E-3 | -552.459 E-3 | 534.940 E-3 | Saturation magnetization maximum M measured |
| M at Hmax (emu/g) | 517.420 E-3 | -552.459 E-3 | 534.940 E-3 | Magnetization at maximum field |
| Hmax(Oe) | 22000.773 | -24032.466 | 23016.619 | Maximum H measured |
| Slope at Hc (emu/g .Oe) | 0.002 | 0.002 | 0.002 | Slope at Hc |
| Slope (emu/g.Oe) | 28.096 E-6 | 28.252 E-6 | 28.174 E-6 | Slope of linear interpolation of all data points |
| Susceptibility (CGS) | 31.347 E-3 | 31.521 E-3 | 31.434 E-3 | Susceptibility calculated from solpe in CGS unitless |
| Susceptibility (SI) | 393.919 E-3 | 396.103 E-3 | 395.009 E-3 | Susceptibility calculated from solpe in SI unitless |
| Permiability CGS slope | 1.394 | 1.396 | 1.395 | Permiability calculated from slope in CGS unitless |
| Permiability SI slope (H/m) | 1.75E-06 | 1.754 E-6 | 1.753 E-6 | Permiability calculated from slope in SI (H/m) |
| Hk (Oe) | 327.642 | -345.872 | 336.757 | Anisotropy field calculated from intersection of slope at Hc and Ms |
| Hs (Oe) | 22201.2 | -22000.76 | 21110.98 | Saturation field at wich M reaches 0.95 Ms |
| Hn (Oe) | 22241.07 | 20204.25 | 21222.66 | Nucleation field: Field where M starts to drop saturation (M = 0.95Ms) |
| H1(Oe) | 19.39 | -19.57 | 19.48 | Field where M(H1) = 0.5 Mr |
Virgin magnetization curve
Figure 3b shows the virgin magnetization curves at room temperature (T=25°C). Starting from the demagnetized state (H=0, M=0) the magnetization increases with the applied H. In the virgin state H=0, the magnetic domains with positive magnetization combine with those with negative magnetization so that the total magnetization of the system is zero. As H increases, domains with magnetization oriented in the same direction of the exciting field increase in volume at the expense of domains with magnetization oriented opposite to the direction of the applied field. Finally, the magnetized domains in the opposite direction to the direction of H are eliminated, thus leading to saturation of magnetization. It is shown that the saturation of magnetization is not affected for the investigated compound.
Mathematical Rayleigh calculation
Rayleigh region is the first part of the initial magnetization curve, where low magnetizing fields are acting on the material. In this region, initial magnetization curve is a parabolic curve described by second order polynomial equation called Rayleigh law [36, 37]:

Where B is the magnetic flux density, H is the magnetizing field, μ0 is the magnetic permeability of free space, μi is the initial relative magnetic permeability, αR is called Rayleigh coefficient and M is the magnetization.
Linear dependence between relative magnetic permeability μ and magnetizing field is given [38]:

The magnetization can be expressed as a function of the applied field H according to the Raleigh law [37-38]:

Where M is the magnetization, H is the internal field, χ0 is the initial susceptibility and α is the Rayleigh constant. The initial magnetic susceptibility and Rayleigh constant are the parameters which depending on the properties of the materials (Table 3).
TABLE 3 Experimental magnetic parameters from the virgin curve
| Parameters from Virgin curve | Average | Definition |
|---|---|---|
| Hc(Oe) | 3520.582 | Corcitive field of virgin curve: H at M = 0.5Ms |
| Ms | 5.164 E-1 | Saturation magnetization: maximum M measured |
| Hs (Oe) | 20247.251 | Saturation field for the virgin curve: field at which M (H) reaches 0.95Ms |
| Area_vir (Oe*emu/g) | NaN | Area under the virgin curve |
| Perm_0 (emu/Oe) | 1.08E-06 | Initial permiability |
| M at H maximum | 5.164 E-1 | M at maximum field |
| M/Ms(%) | 0.63 | M/Ms (%) at H=0.00 |
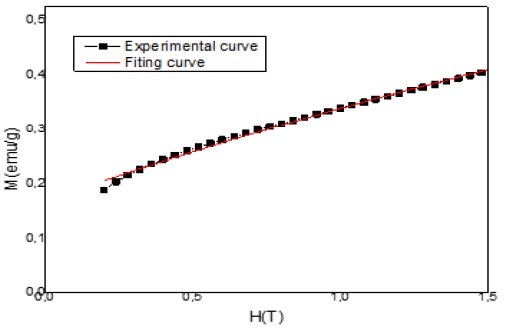
Figure 4 show the magnetization fitted curve according to the Raleigh law. The fitting parameters for the LaNi3.6Al0.3Mn0.4Co0.7 are summarized in Table 4. The value of the susceptibilities found from fitting is in good agreement with the experimental value.
TABLE 4 Calculated parameters from fitting of the LaNi5 and LaNi3.6Al0.4Co0.7Mn0.3 intermetallic compounds according to the Raleiyh law
| χ0(εμυ/γ) | χ0(εμυ/γ) | α(εμυ/γ) | |
| Experimental value | From fitting | From fitting | |
| LaNi3.6Al0.4Co0.7Mn0.3 | 0.39 | 0.3 | -0.01 |
In the present case, the value of the susceptibility of the intermetallic compound confirms that the intermetallic is paramagnetic.
The Rayleigh constant is negative at low temperatures. The negative value confirms that the two materials are magnetically soft [39]. This means that in each particle when the magnetization is reversed, there are no potential barriers for the motion of the domain walls of the initial multi-domain state of the particle [40].
Hydrogen storage reaction under the action of the electromagnetic field
The pressure sensor installed between the reactor bed and the hydrogen tank measures a voltage difference. This pressure difference is converted to a pressure using equation 5:
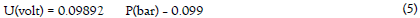
• Hydrogen absorbed / desorbed mass calculation
It is assumed that hydrogen behaves like an ideal gas in the temperature ranges (0°C-100°C) and at pressures below 15 bars.
A gram atom of hydrogen at temperature T (°K) and pressure P (atm) occupies the volume:

With T0=273°K, Patm=1.0133 bar, Va is the total volume of the buffer tank, pipes and free space in the reactor, Va is estimated equal to 11207 cm3.
The number of atoms gram of hydrogen in a volume V at a temperature T and a pressure P is given by:

During absorption, the number of gram atoms of hydrogen at time t = 0 s is given by:
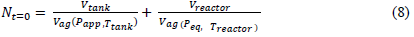
At a time t, the number of gram atoms of hydrogen in the two free volumes of the tank and the reactor is given by:

Where T0 is the initial temperature used in K, P (t) is the applied pressure in the tank.
The number of gram atoms of hydrogen absorbed and desorbed is given by:
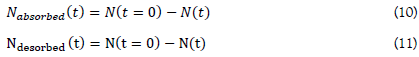
The absorbed and desorbed hydrogen concentrations are then given by:
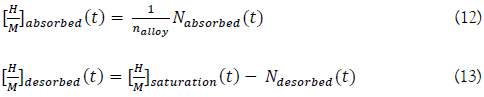
Finally, the mass of absorbed and desorbed hydrogen are given by:
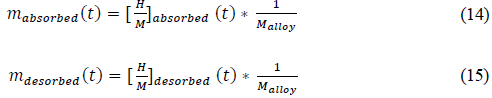
• Absorption reaction
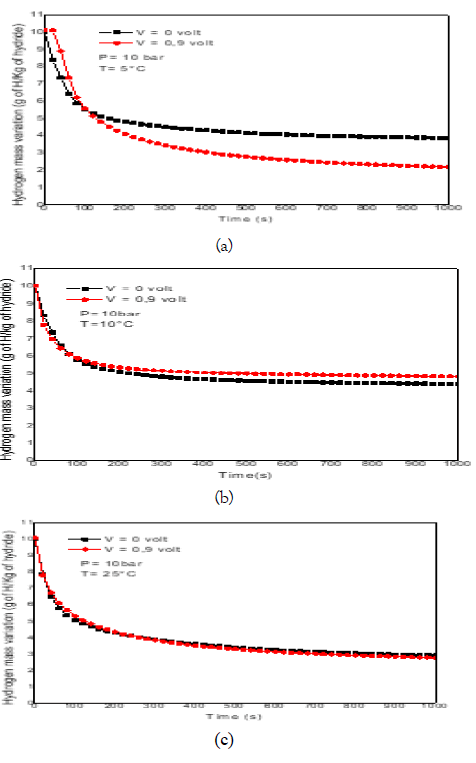
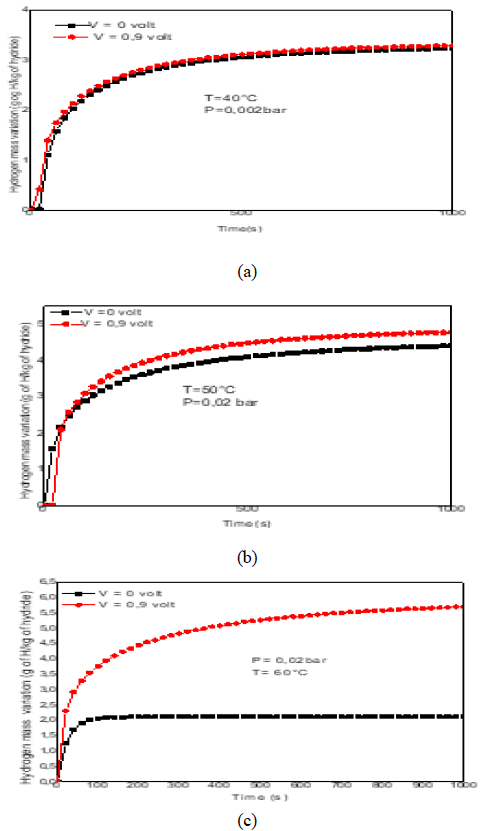
The hydrogen absorbed mass is calculated according to eq.14. Figure 5(a-c) represent the hydrogen mass variationduring absorption reaction as a function of initialtemperature and magnetic field. Results show that theapplied electromagnetic field does not promote theabsorption reaction. It is observed that in the case of lowtemperature (T=5°C), the mass of hydrogen absorbed isconsiderably affected by the applied field. The increase intemperature suppresses the electromagnetic effect. This isexplained by the fact that at low temperature, the magneticfield applied causes a disorder which blocks the reaction.
• Desorption reaction
The desorbed hydrogen mass is calculated using eq. 15.Figure 6(a-c) represent the hydrogen mass variation duringdesorption reaction. It is observed that the appliedmagnetic field does not affect the desorption reaction at40°C and 50°C. However, it promote the reaction at 60°C.
Conclusion
The magnetic properties of the LaNi3.6Al0.4Mn0.3Co0.7 at room temperature have been determinate and the magnetic parameters have been calculated. The hydrogen storage properties under the action of an electromagnetic field have been considered. Results showed that the compound is a paramagnetic compound. It is classified as magnetically soft. The applied magnetic field disfavor the absorption hydrogen reaction and promote the desorption reaction.
References
- Van V, Kuijpers F, Bruning H. Reversible room-temperature absorption of large quantities of hydrogen by intermetallic compounds. Philips res rep. 1970:25;133-40.
- Jose B, Jose RA, Jussara B, et al. Application of hydrides in hydrogen storage and compression: Achievements, outlook and perspectives. Int J Hydrog Energy. 2019:44(15);7780-808.
- Louis S, Andreas Z. Hydrogen-storage materials for mobile applications. Insight rev artic. 2001:414;338-44. Google Scholar]
[Crossref]
- Manmeet K,Kaushi k. Review on hydrogen storage materials and methods from an electrochemical viewpoint. J Energy Storage. 2019:23;234-49.
- Reilly JJ, Wiswall RH. Formation and Properties of Iron Titanium Hydride. Inorg chem. 1974; 13:218-22.
- Tan S, Ors T, Akyildiz H, et al. Synthesis of FeTi Hydrogen Storage Alloys for Stationary Applications. Proc 2nd Int Hydrog Energy Congr Exhib IHEC. 2007:13-15.
- Livramento V, Rangel CM, Correia JB, et al. Synthesis of FeTi hydrogen storage material via ball milling: effect of milling energy and atmosphere. Int Workshop Adv Fuel Cells Hydrog Econ. 2008.
- Liang G, Huot J, Schulz R. Hydrogen storage properties of the mechanically alloyed LaNi5-based materials. J Alloys Compd. 2001:320;133-39. [Google Scholar] [Crossref]
- Nahm KS, Kim WY, Hong SP, et al. The reaction kinetics of hydrogen storage in LaNi. Int J Hydrog Energy. 1992:17;333-38.
- Wallace WE, Karlicek RF, Imamura H. Mechanism of Hydrogen absorption by LaNi5. J Phys Chem. 1979:83:1708.
- Yang Y, Yi Y, Jianfeng L, et al. Enhanced hydrogen storage of a LaNi5 based reactor by using phase change materials. Renew Energy. 2021:180;734-43.
- Uday R, Satyasekhar B. Performance analysis of LaNi5 added with expanded natural graphite for hydrogen storage system. Int J Hydrog Energy. 2023:48;21466-75.
- Hongen Y, Yong W, Shunpeng C, et al. Pd-modified LaNi5 nanoparticles for efficient hydrogen storage in a carbazole type liquid organic hydrogen carrier. Appl Catal B: Environ. 2022:317; 121720.
- Atef C, Aissa D, Leila N, et al. Upscaling of LaNi5-based metal hydride reactor for solid-state hydrogen storage: numerical simulation of the absorption–desorption cyclic processes. Green Approach Altern Fuel Sustain Future. 2023:257-269.
- Dhaou H, Souahlia A, Mellouli S, et al. Experimental study of a metal hydride vessel based on a finned spiral heat exchanger. Int J Hydrog energy. 2010:35;1674-80
- Souahlia A, Dhaou H, Askri F, et al. Experimental and comparative study of metal hydride hydrogen tanks. Int J Hydrog energy. 2011:36;12918-22
- Satyaki C, Pratibha S, Sankara S, et al. Modeling and numerical simulation of a 5 kg LaNi5-based hydrogen storage reactor with internal conical fins. Int J Hydrog energy. 2020:45;8794-809.
- Yang Y, Yi Y, Jianfeng L, et al. Enhanced hydrogen storage of a LaNi5 based reactor by using phase change materials. Renew Energy. 2021:180;734-43.
- Yang Y, Jianfeng L, Jing D, et al. Performance improvement of metal hydride hydrogen storage tanks by using phase change materials. Appl Energy. 2022:320;119290.
- Busra A, Mustafa I, Selahattin C. Experimental analysis of hydrogen storage performance of a LaNi5–H2 reactor with phase change materials. Int J Hydrog energy. 2023:48;6010-22.
- Uday R, Satyasekhar B. Performance analysis of LaNi5 added with expanded natural graphite for hydrogen storage system. Int J Hydrog energy. 2023:48;21466-475.
- Fusheng Y, Xinxin C , Zaoxiao Z , et al. Assessment on the long term performance of a LaNi5 based hydrogen storage system. Energy Procedia. 2012:29;720-30.
- Jose J, Daniel R , Ricardo F, et al. Hydrogen storage in MgH2eLaNi5 composites prepared by cold rolling under inert atmosphere. Int J Hydrog energy. 2018:43;13348-55.
- Sakintunaa B, Lamari-Darkrimb F, Hirscherc M. Metal hydride materials for solid hydrogen storage: A review. c. 2007:32;1121-40.
- Sumita S, Kuldeep P. Effect of transition metals on ball-milled MmNi5 hydrogen storage alloy. J. Mater Renew Sustain Energy. 2015:4;19.
- Kwo hY, Jean N. The Current Status of Hydrogen Storage Alloy Development for Electrochemical Applications. J Mater. 2013:6;4574-4608.
- Borzone EM, Blanco MV, Baruj A, et al. Stability of LaNi5−xSnx cycled in hydrogen. Int J Hydrog energy. 2014:39;8791–96.
- Oliva G, Fuentes M, Borzone EM, et al. Hydrogen storage on LaNi5−xSnx. Experimental and phenomenological Model-based analysis. Energy Convers Manag. 2018:173;113-22.
- Zhida Z, Shuai Z, Haoqi L, et al. Stability of LaNi5-xCox alloys cycled in hydrogen — Part 1 evolution in gaseous hydrogen storage performance. Int J Hydrog energy. 2019:44;15159-72.
- Joubert JM, Cermy R, Latroche M, et al. A structural study of the homogeneity domain of LaNi5. J state chem. 2002:166;1-6.
- Dhaou H, Belkhiria S, Sdiri N, et al. Thermodynamic and electric study of the LaNi3,6Al0,4Co0,7Mn0,3 alloy. Int J Hydrog energy. 2016:42;2209-14.
- Briki C, Askri F, Jemni A, et al. Dynamic study of a new design of a tanks based on metallic hydrides. Int J Hydrog energy. 2018:43;1566-76.
- Briki C, Belkhiria S, Dhaou M, et al. Experimental study of the influences substitution from Ni by Co, Al and Mn on the hydrogen storage properties of LaNi3.6Mn0.3Al0.4Co0.7 alloy. Int J Hydrog energy. 2017:42;10081-88.
- Belkhiria S, Briki C, Dhaou H, et al. Experimental study of metal–hydrogen reactor behavior during desorption under heating by electromagnetic induction. Int J Hydrog energy. 2017:42; 16645-56.
- Belkhiria S, Briki C, Dhaou H, et al. Experimental study of a metal –hydrogen reactor behavior’s subjected under the action of an external magnetostatic field during absorption and desorption. Int J Hydrog energy. 2020:45;4673-84.
- Maciej K. Measurement system for investigating magnetic characteristics of soft magnetic materials in Rayleigh region. Inst Metrol Biomed Eng. 2015.
- Kachniarz M, Szewczyk R. Study on the Rayleigh Hysteresis Model and its Applicability in Modeling Magnetic Hysteresis Phenomenon in Ferromagnetic Materials. Acta Phys Pol Ser. 2017:131;1244-50. [Google Scholar] [Crossref]
- Kachniarz M, Salach J, Roman S. Investigation of Magnetic Properties of Amorphous Fe-Based Alloy Magnetized in Rayleigh Region. Int Conf Mechatron. 2018. [Google Scholar] [Crossref]
- Andrii V, Alexander B, Viktor M, et al. Temperature-dependent magnetic properties of a magnetoactive elastomer: Immobilization of the soft-magnetic filler. J Appl Phys. 2018:123;115118.
- Bodnaruk A, Brunhuber A, Kalita M, et al. Temperature-dependent magnetic properties of a magnetoactive elastomer: immobilization of the soft-magnetic filler. J Appl Phys. 2018:123;115118.