On the Bell Experiment and Quantum Foundation

Received: 17-May-2023, Manuscript No. puljmap-23-6446; Editor assigned: 19-May-2023, Pre QC No. puljmap-23-6446(PQ); Accepted Date: May 28, 2023; Reviewed: 22-May-2023 QC No. puljmap-23-6446(Q); Revised: 25-May-2023, Manuscript No. puljmap-23-6446(R); Published: 01-Jun-2023, DOI: 10.37532/ puljmap.2023.6(2);01-05

Citation: Helland IS. On the bell experiment and quantum foundation. J Mod Appl Phys. 2023; 6(2):1-5.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

The Bell experiment is discussed in light of a new approach towards the foundation of quantum mechanics. It is concluded from the basic model that the mind of any observer must be limited in some way: In certain contexts, he is simply not able to keep enough variables in his mind when making decisions. This has consequences for Bell’s theorem, but it also seems to have wider consequences.

Key Words

Accessible variables, Bell experiment, CHSH inequality, Conceptual variables, Inaccessible variables, Mathematical models, Mind of an observer, Quantum foundation.

Introduction

The Nobel Prize in Physics for 2022 for performing different versions of the Bell experiment was well deserved. But despite an enormous literature on the subject, a real understanding of the result of the experiment is still lacking. The purpose of this article is to propose a solution, not by being a Bell denier, and not by assuming some action at a distance, but simply by departing from a general realist view of the world. In my opinion, every description of a physical phenomenon must be from the point of view of an observer or from the point of view of a group of communicating observers.

Let me mention briefly my background. I am not a physicist, I am a statistician, and my main aim has been to find some basis for the quantum theory that I am able to explain to my fellows, the statisticians. As a step towards doing this, I published on Springer in 2018 the book ’Epistemic Processes’. Later I discovered that Chapter 4 in that book was incomplete and even contained an error in the discussion of spins. These errors are now been corrected in a revised 2021 edition of the book. I have also published a number of articles related to my views on quantum foundations; some of these articles are collected in the book [1]. All the mathematical arguments are now gathered in the article Helland [2].

However, the main problems of quantum mechanics are not simply related to mathematics, but to what mathematics describes.

Central notions for me are the questions that we ask nature. As long as we are very small children, we approach nature only by way of our interaction with other people, say our parents. But as we grow older, we start to ask questions. There seem to be some adults who have stopped asking questions and only have opinions. These opinions may be based on their free will, but also perhaps upon looking up to certain authorities. I tend to look up to Einstein and some other similar authorities. I see Albert Einstein as a great genius, but I do not agree with his opinions about quantum mechanics. There are still physicists that wanted to abolish the whole of quantum mechanics, but I strongly disagree with such views.

The whole of empirical science is in reality the field of asking questions to nature and trying to obtain answers. The purpose of statistics is to help empirical science in this process. In some way, I feel that there should be a connection between theoretical sciences whose purpose is related to the study of nature on the one hand and statistical theory on the other hand. This is one point of departure from my books and papers.

To me, it is also natural that an ultimate quantum theory should be related to asking questions about nature. The first problem raised in my note is whether this is the case with the existing quantum theory [3]. And the answer to this seems largely to be affirmative. For spin components in the spin 1/2 case, the one-to-one correspondence between quantum states on the one hand, and question-and-answer pairs on the other hand seems to be quite clear. This is proved more generally [1,4,5].

This is the way I try to approach quantum theory in my books and in my papers: Through accessible conceptual variables. The basic notion is that of conceptual variables, which are related to the mind of an observer or to the joint minds of a group of communicating observers.

It is really simple: In a spin 1/2 situation, for instance, an accessible conceptual variable is nothing but the spin component in a given direction as perceived by an observer (or by communicating observers). But the full spin vector is inaccessible to any observer. Having a purely epistemic approach towards quantum mechanics, it seems possible to understand so-called paradoxes like Schrödinger’s cat, Wigner’s friend, and the two-slit experiment. I have my own solutions, based on a version of quantum mechanics where the only allowable pure-state vectors are those which are eigenvectors of some physically meaningful operator [2].

In my approach to the born formula, I assume that the actor in question has an authority that can be said to be perfectly rational [4]. Understanding this more properly seems to be a more interesting task than continuing the discussion around the Bell inequalities, which we now know are violated by nature. But I will try to summarize my views on the latter issue here. In my view, seeking a theory that covers reality in all situations - whatever that means, seems to be impossible. We are not gods. Instead, in my opinion, we should be looking for a theory that is related to our knowledge of reality. Any process of seeking knowledge can be called an epistemic process.

Quantum theory should be seen as a mathematical model, a model related to the mind of an observer, or to the joint minds of a communicating group of observers.

Consider the Bell situation. To an observer Charlie, receiving data from both Alice and Bob, there are two accessible conceptual variables: The spin component as perceived by Alice, and the spin component as perceived by Bob. Alice and Bob are not communicating. Alice has free will to choose the direction in which she wants to measure the spin component, and so has Bob. Then they achieve their responses. Quantum theory is related to these perceived responses. Bell’s inequality has to do with a hypothetical reality behind these measurements, and this, in my opinion, is a reality that we do not seem to be able to cover completely with any ordinary human-made model. As I see it, this is in some way all there is to it.

This article can be seen as a shorter and improved version [6].

The bell experiment

Two observers Alice and Bob are space likely separated at the moment when they observe. Midways between them is a source of entangled spin 1/2 particles, one particle in a pair is sent towards Alice, the other towards Bob. In concrete terms, the joint state of the two particles is given by

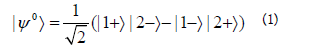
Here and in the following the spin component in any direction is normalized to ±1. In (1) |1u⟩ means that the spin component of particle 1 in some fixed (z) direction is u, while| 2vâ?ª means that the spin component of particle 2 in the z-direction is v. This state expresses that the total spin of the two particles is 0. One can imagine that these particles previously have been together in some bound state with spin 0.

Alice is given the choice between measuring the spin component of her particle in one of two directions a or a’. If she measures in the adirection, her response (± 1) is called A, and if she measures in the a’ direction, her response is called A’. Similarly, Bob can measure in one of two directions b (giving a response B) or b’ (giving a response B’). The whole procedure is repeated n times with different entangled particle pairs and with different directions/ settings chosen by Alice and Bob.

We now temporarily take the point of departure that all these response variables exist in some sense. This can be seen as an assumption of realism. At the very least, we will assume that this point of departure is meaningful for some observers or for a group of communicating observers.

Since all responses then are ±1, we then have the inequality

The argument for this is simply: B and B’ are either equal to one another or unequal. In the first case B− B' = 0 and B + B'=±2 ; in the last case B− B' =±2 and B + B' = 0 .Therefore, AB+A’B +AB’ −A’B’ is equal to either A or A’, both of these being ± 1, multiplied by ± 2.

All possibilities lead to A+ A^'B+ AB^'+ A^'B^'− B =±2

From this, a statistician will argue: Assume that we can consider A, A^',B and B^' as random variables, defined on the same probability space (Ω,F, P,) . Then by taking expectations over the terms in (2),

we find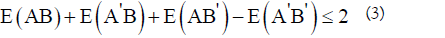

A physicist will have a related argument: Assume that there is a hidden variable λ such that 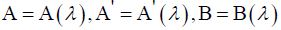and ' B' = B'(λ ). The assumption that such a hidden variable exists, is called local realism in the physical literature.

By integrating over the probability distribution ρ of λ, this gives

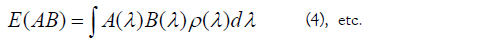
Thus, by integrating the term for the term in (2), we again find (3). Of course, the above two arguments are equivalent; it is just a question of using either the notation (ω,P) or (λ,ρ).

There are different traditions here. These arguments are reviewed and discussed in detail [7].

The inequality (3) is called the CHSH inequality after the authors and has been the source of much controversy [8]. First, it is known that if we use quantum mechanics to model the above experiment, one can find settings such that the CHSH inequality is violated. Secondly, recent loophole-free experiments, taken together with the experiments done by the 2022 Nobel laureates in physics) have shown that the CHSH inequality may be violated in practice [9-14].

Thus, the simple assumptions sketched above for (3) cannot hold.

The Hilbert space formulation from two different maximal accessible variables

A completely new approach toward quantum foundations is proposed [4,6,11,1,2]. The basis is a model of an observer’s mind when this observer is in some physical situation. In this situation, there are physical variables, and the observer will have at least some of these variables, say θ,λ,η, in his mind. Some of the variables are accessible to him, that is, it is, in some future, in principle possible to obtain as accurate values as he wishes on the relevant variable. Others are inaccessible. Examples of the latter are the vector (position, momentum) of a particle at some time, or the full spin vector of a spin particle.

The main assumption in the new model is as follows: Related to the mind of an observer A, there is an inaccessible variable φ such that all accessible variables can be seen as functions of φ. In the two examples above one can take φ=(theoretical position, theoretical momentum) and φ = full spin vector. In the last example, in the spin 1/2 case, one can model the discrete spin component in the direction an assign (cos(a,φ)), and let φ have a uniform distribution on the sphere. Here these variables are physical variables, but following every description of reality must be seen relative to the mind of some observer [12,13]. Hence we can assume that the variables also exist in the mind of A. In these two examples, there are also maximally accessible variables

In the first example either position or momentum, in the second example the spin component θ and in some direction a. In general, an accessible variable θ is maximal for an observer at time t if there is no other accessible variable λ at this time for the observer such that θ = f(λ) for some non-invertible function f.

Two accessible variables θ and η are said to be related if there is a transformation k in φ-space and a function f such that θ = f (θ) and n = f (kθ ) . In it is shown that if both θ and η are maximal and take r values, then φ can be constructed in a natural way such that θ and η are related with respect to this φ. In particular, two spin components θ_a and θ_b are related with respect to the total spin vector [2].

If no such transformation k can be found for a given φ, we say that θ and η are essentially different with respect to this φ.

In the present paper, we will concentrate on accessible variables that take a finite number of values. Then the following is proved in the above papers: Given a situation with two related maximal accessible variables, there corresponds to every accessible variable a self-adjoint operator in some Hilbert space H. Under some weak technical assumptions it can be proved that the eigenvalues of this operator are the possible values of the variable, say θ, and that the eigenspaces are in one-to-one correspondence with questions ‘What is θ?’ together with sharp answers ‘θ = u’. A variable is maximal if and only if all eigenspaces of the corresponding operator are one-dimensional.

The proof of this result relies on constructing a group N acting upon ψ = (θ,η), where θ and η are assumed to be related maximal accessible variables, and a certain representation W(·) of this group which is proved to be irreducible.

This is the first step in a new proposed foundation of quantum theory.

The second step is more technical. One must define a group of actions K upon the φ-space. The function f in ϕ = f ( θ) is said to be permissible with respect to this group if 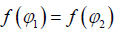implies 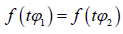. Assume that the two related variables θ and η both are defined by permissible functions. Let T (·) be a multivariate unitary representation of the group K such that the coherent states T ( t ) |v ⟩ for some vector | v⟩; in the actual Hilbert space are in one-to-one correspondence with t ∈ K. Then one can show that if A^θ is the operator corresponding to θ = f (tϕ), then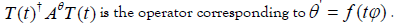

It is shown that in the finite-dimensional case, one can construct group K in such a way that the technical assumptions above are satisfied [2]. One can also show the following If k is the transformation connecting two related variables θ and η, then there is a unitary transformation W(k) such that

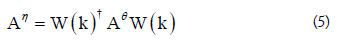
On the other hand, if (5) hold between two operators, then the corresponding variables θ and η are related. This is proved by the following lemma [2].

Lemma: Consider two maximal accessible finite-dimensional conceptual variables θ and λ. If there is a transformation s of Ωψ such that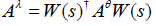

Proof: By equation (26) the relation implies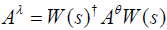

that

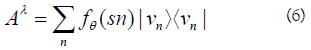           [2]

for an orthonormal basis 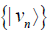for which we also have

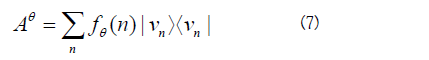
But by the spectral theorem, we also have

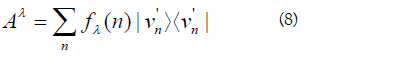
for some orthonormal basis. Since all the accessible variables are maximal, the eigenspaces are one-dimensional by Theorem A2 of [12]. In particular, this means that since Aλ has a spectral decomposition in one basis in (6), the same basis must be used in (8). This also implies

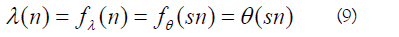
so θ and λ are related with respect to the group N. Since by the model, each variable is a function of the inaccessible variable φ, they must also be related with respect to φ.

Given the results above, a rich theory follows. The set of eigenvalues of the operator A^θ is identical to the set of possible values of θ. The variable θ is maximal if and only if all eigenvalues are simple. In general, the eigenspaces of A^θ are in one-to-one correspondence with questions ‘What is θ’/‘What will θ be if we measure it?’ together with sharp answers θ = u.

This points at a new foundation of quantum theory and suggests a general epistemic interpretation of the theory: Quantum theory is not directly a theory about the world, but a theory about an actor’s knowledge of the world. From this conclusion also a number of socalled ‘quantum paradoxes’ can be solved (assuming a version of quantum theory in which the only acceptable pure states are those which are eigenvectors of some physically meaningful operator), see [11].

Limitation in the mind of an observer in some context

Let an observer O be in some physical context. In agreement with his observations and planned observations, he will have several physical variables θ,η,λ, in his mind. I will assume here that all these variables are finite-dimensional. According to my general model, these variables can all be seen as functions of a fixed inaccessible variable φ. Then we have the following

Theorem 1: Assume that O has two related maximal accessible variables θ and η in his mind at some fixed time t. Then he cannot simultaneously have in his mind another maximally accessible variable that is related to θ, but essentially different from η.

Proof: Denote the new variable by λ. Let the transformation relating θ and η be k, and the transformation relating θ and λ be s. Then by (5) we have 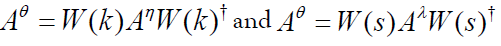. But this implies that 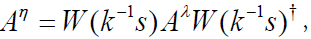so we conclude from the Lemma of the previous Section that η and λ are related, which leads to a contradiction with the assumptions made.

Note: It is essentially here that a fixed context is assumed, and that the time t is kept fixed. If we allow time to vary, O can have in mind a large number of variables, also essentially different ones. Also, note that O here can be any person

Limitations in the mind of Charlie

Assume that Alice and Bob have made n independent repetitions of the Bell experiment, each time choosing their settings either by their own free will or by some random mechanism. After this, they leave all their data to a statistician Charlie, who will try to make a statistical model of the experiment.

To this end, he thinks of a typical experiment, with setting either a or a’ chosen by Alice, giving corresponding responses A or A’, each either -1 or +1, and similar settings b or b’ chosen by Bob, with responses B and B’. As a good statistician, he relies on the conditionality principle and wants to condition his model upon all the settings, only modelling the possible responses [14].

The inaccessible variables, in this case, are the full spin vector φ_A of Alice’s particle and the full spin particle φ_B of Bob’s particle. To Charlie, both these are inaccessible, but at the same time, he knows from other experiments that if Alice and Bob measure spin in the same direction, then their spin components are opposite. Thus, in his mind, he may think of a model where ϕ_B = −ϕ_A , in the sense that any measured components are opposite. For a precise statement and proof based upon the entangled state vector (1), see the next Section.

The goal of Charlie is to formulate a model for the possible responses A, A’, B and B’. Each of these variables takes the values -1 or +1, and each is maximal as a variable that is accessible to respectively Alice and Bob. For Charlie, we will see that the variables are pairwise related under the model. During his modelling attempts, he is able to communicate with Alice and Bob. The term ‘accessible’ will be defined with respect to this whole set of communicating actors, meaning that a variable is called accessible if it at the outset also has been accessible either to Alice or to Bob. In this sense, each of the variables A, A’, B, and B’ must be seen as maximal accessible.

Theorem 2: Under these assumptions, in relation to Charlie’s model of the variables A, A’, B, and B’, the following hold:

• All the pairs of variables are related under his model.

• Given two such pairs which share one variable, the fourth variable will be related to the variables of both pairs, but essentially different from another variable, a function of the variables in the two pairs

Proof:

1) Look first at a pair associated with the same primitive observer, say, Alice, so the variables are A and A’. These are spin components in different directions, and Charlie can have, as an inaccessible part of his model, the projection λ of Alice’s spin vector upon the plane spent by these two directions.

Let k be a suitable rotation of λ in this plane. Then for some value of λ and for some function f, we have A = f(λ) and A’ = f(k λ). Explicitly, the function f can be taken as f(λ) = sign(cos(a, λ)).

Then look upon a pair of variables from both primitive observers, which possibly can be measured in the same run, say A and B. Then by what has been proved above, A is related to a hypothetical variable A”, measured by Alice in the Bob-direction b, which is known to her. But, by Charlie’s mental model, he must conclude that A”= −B, hence A and B are related.

2) Say that the two pairs are (A,B) and (A,B’) so that the fourth variable is A’. Then A’ is related to both variables in the first pair, and to both variables in the second pair by 1 above. Now look at the variableC= A ( B+B'). This variable takes the value 0 if B = −B’, and the values ±2 if B = B’. This variable is determined by the joint values of A, B, and B’, but is quite unrelated to the value of A’. Thus, we must conclude that C and A’ are essentially different; they cannot be coupled by any transformation in Charlie’s φ-space.

Corollary 1: Charlie is not able to keep all four variables A, A’, B, and B’ in his mind at the same time t during the modeling process. Note that Charlie may be a statistician, and he may be able to communicate with any person. This person may be interested in the Bell experiment, and he may after the experiment have had contact with Alice and Bob, and have listened to their experiences.

Corollary 2: For any communicating person there may exist situations where he is not able to keep in hIn particular, this seems to happen for any person trying in practice in a concrete context to reproduce the simple argument leading to (3) in Section 2 above in a way that can be communicated to all people, including the actors Alice and Bob at a time when they make Bell experiments, taking into account their limitations at such times.is mind all the variables that he is exposed to.

The state of Charlie

Consider two spins 1/2 particles, originally in the state of total spin 0, then separated, one particle sent to Alice and one particle sent to Bob. This can be described by the entangled singlet state (1).

As in David Bohm’s version of the EPR situation, let Alice measure the spin component of her particle in some direction, and let Bob measure the spin component of his particle in the same direction. As has been described in numerous papers, there seemingly is an action at a distance: The spin components are always opposite.

I want to couple this with the philosophy of Convivial Solipsism: Every description of the world must be relative to the mind of some actor. So let us introduce an actor, Charlie, observing the results of both Alice and Bob. Charlie’s state during this observation is given by (1).

Let us try to describe all this in terms of accessible and inaccessible variables. The unit spin vectors φ_A and φ_B of the two particles are certainly inaccessible to Charlie, but it turns out that their dot product η = φ_A · φ_B is accessible to him. In fact, Charlie is forced to be in the state given by η=−3.

Mathematically this is proved as follows. The eigenvalues of the operator Aη corresponding to η are 1 and -3. The eigenvector associated with the eigenvalue -3 is just |ψ0 ⟩ of (1), while the eigenspace associated with the eigenvalue 1 is three-dimensional [15]. (See for instance exercise 6.9. page 181 in Susskind and Friedman, 2014.)

What does it mean that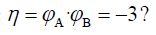

It means that for the components in the x, y, and z directions, we have 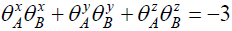and since all components here are either -1 or +1, this is only possible if 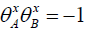etc. which implies

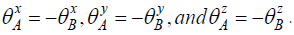It follows that 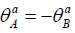in every direction a

Note that Charlie here can be any person. So we conclude: To any observing person, the spin components as measured by Alice and Bob must be opposite in this situation. This is a necessary conclusion, implied by the fact that the person, relative to his observations, is in the state given by (1).

Bell’s theorem

There are many variants of Bell’s theorem in the literature, and the theorem has led to several rather complicated discussions among theoretical physicists [16]. According to Wikipedia, the theorem has two components: Physical variables exist independently of being observed or measured (sometimes called the assumption of realism); and second, that Alice’s choice of action cannot influence Bob’s result or vice versa (often called the assumption of locality).

Bell’s theorem then says that these two assumptions imply that the Bell inequality/ CHSH inequality hold whenever a Bell experiment is performed. So when we now know for sure that this inequality may be violated in practice, one of the assumptions must be abandoned.

From the discussion above, it seems that it is the assumption of realism which must in some way be given up. My own point of departure is Hervé Zwirn’s Convivial Solipsism. Every description of reality must be relative to the mind of an actor (or relative to the joint minds of a communicating group of actors) [1,13]. To be in agreement with observations, we seem to be forced to the conclusion that the minds of these actors must be limited in certain contexts.

Result

So assume in general that Alice and Bob belong to different groups of people that do not communicate, and they both make a series of decisions, say dichotomous ones, and these decisions have consequences, which are accessible to Alice and Bob, respectively, in the situation, and in a certain sense maximally so. Later, the consequences may be accessible to outsiders.

Such general descriptions may seem to be relevant to certain political and social situations. An outsider may try to make deep enough scientific models of the whole situation, models that also can be explained to both parties in the relevant context. According to the theory of this paper, such endeavors will be demanding: The outsider may have difficulties keeping enough variables in his mind.

I will not here go further into which political and social situations I am thinking of. It is well known that quantum theory may be used to model the process of making decisions, see for instance [17].

Conclusions

Let us try to recapitulate. The Bell experiment has to do with two actors Alice and Bob who cannot communicate during the experiment. They both make dichotomous decisions on their settings of some apparatus, and they both observe dichotomous responses. For any actor who tries to understand these responses, according to the theory, his mind must be limited: He is simply not able to keep enough variables in his mind at the same time

If this is true, it also must have consequences for other situations.

References

1. Helland, I.S. On the Foundation of Quantum Theory. 2023.
2. Helland IS. An alternative foundation of quantum mechanics. ArXiv. 2023.

   [Google scholar] [Crossref]

3. Helland IS. When is a set of questions to nature together with sharp answers to those questions in one-to-one correspondence with a set of quantum states? ArXiv. 2019.

   [Google scholar] [Crossref]

4. Helland IS. Epistemic processes. Springer International Publishing; 2021.

   [Google scholar]

5. Höhn PA, Wever CS. Quantum theory from questions. Physical Review A. 2017; 95(1):012102.

   [Google scholar] [Crossref]

6. Helland IS. The Bell experiment and the limitations of actors. Foundations of Physics. 2022; 52(3):55.

   [Google scholar] [Crossref]

7. Gill RD. Statistics, causality and Bell’s theorem. 2014; 20 (4): 512-528.

   [Google scholar] [Crossref]

8. Clauser JF, Horne MA, Shimony A, et al. Proposed experiment to test local hidden-variable theories. Physical review letters. 1969; 23(15):880.

   [Google scholar] [Crossref]

9. Giustina M, Versteegh MA, Wengerowsky S, et al. Significant-loophole-free test of Bell’s theorem with entangled photons. Physical review letters. 2015; 115(25):250401.

   [Google scholar] [Crossref]

10. Shalm LK, Meyer-Scott E, Christensen BG, et al. Strong loophole-free test of local realism. Physical review letters. 2015; 115(25):250402.

    [Google scholar] [Crossref]

11. Helland IS. On reconstructing parts of quantum theory from two related maximal conceptual variables. International Journal of Theoretical Physics. 2022; 61(3):69.

    [Google scholar] [Crossref]

12. Zwirn H. The measurement problem: Decoherence and convivial solipsism. Foundations of Physics. 2016; 46:635-67.

    [Google scholar] [Crossref]

13. Zwirn H. Nonlocality versus modified realism. Foundations of Physics. 2020; 50(1):1-26.

    [Google scholar] [Crossref]

14. Cox DR. Some problems connected with statistical inference. Ann. Math. Statist. 1958; 29(2):357-72.

    [Google scholar]

15. Susskind L, Friedman A. Quantum mechanics: the theoretical minimum. Basic Books; 2014.
16. Bell JS. On the einstein podolsky rosen paradox. Physics Physique Fizika. 1964; 1(3):195.

    [Google scholar].

17. Busemeyer JR, Bruza PD. Quantum models of cognition and decision. Cambridge University Press; 2012.

    [Google scholar]