On the riemann hypothesis and the complex numbers of the riemann zeta function

Received: 11-Jun-2023, Manuscript No. puljpam-23-6494; Editor assigned: 15-Jun-2023, Pre QC No. puljpam-23-6494 (PQ); Accepted Date: Jun 26, 2023; Reviewed: 20-Jun-2023 QC No. puljpam-23-6494 (Q); Revised: 05-Jul-2023, Manuscript No. puljpam-23-6494 (R); Published: 30-Sep-2023, DOI: 10.37532/2752-8081.23.7(5).227-228.

Citation: Yoon TC, Yoon Y. On the Riemann hypothesis and the complex numbers of the Riemann zeta function. J Pure Appl Math. 2023; 7(5):227-228.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

The Riemann product formula is provided with the function ζ(s) for all complex numbers from 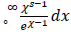by substituting –x only partly for x in the numerator, which is incorrect, because we can find even negative factorials at the same place instead of the so called trivial 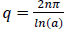from the complex variable z = ±(p + iq) of the Riemann zeta function, which is applicable for all positive and negative planes and complex space including .

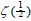Key Words

Riemann Product Formula, Riemann Hypothesis, Riemann Zeta Function, Euler's Delta Function, Negative Factorial

Introduction

The Riemann formula, Bernhard Riemann (1826-1866) suggested the following equation in his paper in 1859 [1].

Where Π(s)=s ! . This Π , named by Gauss (Johann Carl Friedrich Gauss, 1777-1855), has a relationship that Π(s - 1)=Δ(s)=(s- 1) ! with the Euler delta function mentioned below.

This was not something new because Leonhard Euler (1707-1783) presented the following in his paper published after his death in 1794 [2].

Adrien-Marie Legendre (1752-1833) named it Γ function in his paper in 1811 [3].

Riemann has named 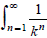as the zeta function. Since the equation (2) is a general formula for n, Riemann’s formula (1) can be indeed expressed as

Euler derived a complex solution for k = p+iq in the equation (2) above, and Riemann attempted to derive a solution for n= p+ iq of (2).

However, Euler’s equation Δ(n) becomes (0 − 1)! at n = 0, and thus has a flow since it is not defined at n = 0. In other words, the below equation is not defined,

and it is the same for Δ(−n). This is to say that the negative factorial is not defined [4].

Therefore, the below equation suggested by Riemann is not correct as well,

It was derived using –x instead of x in the negative domain in calculating s = p + iq

This would be possible under the condition that the negative space is a complex space, but since the complex space also exists in the positive space, it is wrong to derive the equation (7) from the equation (6) where the negative factorial or negative domain is not defined.

If we use the newly defined Euler Y function to rearrange equations including Euler’s Δ function, Gauss’ Pi function, Legendre’s Gamma function, and negative factorial, it will be the following [5].

By using the above, the Riemann equation (1) can be rearranged as the below,

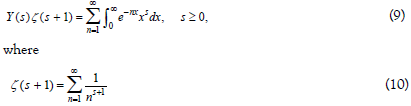
This is effective in the positive area where the domain of s is equal to or greater than zero, and is not effective when using a negative factorial in the negative area.

Although the domain of Riemann zeta function will be greater than 1, since it is indeed effective in all domain, we can change the above equation applying ζ(−s) at the negative domain of −s as below

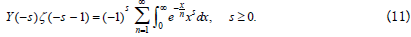
The Riemann equation (6) can be explained with the above equation (11). The complex space for s where s = p + iq, can be derived from the equations including (9), the solutions cannot be found since the 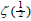which is claimed by Riemann cannot be found in the above formulae (9) and (11).

But, this can be simply drawn from Riemann zeta function.

Complex Numbers of Riemann Hypothesis

As shown above, even Riemann’s formula is effective for all real plane, we are unable to figure out 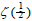from the above. However, we may obtain complex numbers of the Riemann zeta function as follows by using Taylor series. The complex number is defined as

z = ±(p + iq) where p is a real number, q≠0 and i is the imaginary unit. So we obtain,

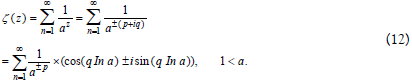
In case a = 1, ζ(z) = 1 denotes the asymptotic line of ζ(z) axis. Even though cosine function of the above is located at −1 ≤ cos(q ln a) ≤ 1, we define q as below, so that q may have always positive value. So far we deal with the Riemann zeta function on the premise so that the complex does not have any impact on the process as if it is always be equal to one. Therefore, we obtain

where, n is an arbitrary integer running from 1 to ∞. This means that at z = ±(p + iq), q exists everywhere independently and innumerably at the same rate for all z of the Riemann zeta function ζ(z). This is effective even if p is equal to zero, i.e., z = iq at ζ(0).

References

1. Riemann B. On the Number of Prime Numbers less than a Given Quantity. 1998  [Google Scholar] [Crossref]
2. Euler L. On the values of integrals extended from the variable term x = 0 up to x = ∞*. 2008  [Google Scholar] [Crossref]
3. Legendre AM. Exercices de calcul intégral sur divers ordres de transcendantes et sur les quadratures. Courcier. 1816.

   [Google Scholar] [Crossref]

4. Davis PJ. Leonhard euler's integral: A historical profile of the gamma function: In memoriam: Milton abramowitz.  Amer Mathe Mon. 1959:1;66(10):849-69

   [Google Scholar] [Crossref]

5. Yoon TC. On the Euler Integral for the positive and negative Factorial. 2020

   [Google Scholar] [Crossref]