How many points are there in a line segment? – A new answer from Discrete-Cellular Space viewpoint

Received: 27-Nov-2017 Accepted Date: Jan 31, 2018; Published: 02-Feb-2018, DOI: 10.37532/2752-8081.18.2.2

Citation: Christianto V, Smarandache F. How many points are there in a line segment? – A new answer from Discrete-Cellular Space viewpoint. J Pur Appl Math. 2018;2(1):1-4.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

While it is known that Euclid’s five axioms include a proposition that a line consists at least of two points, modern geometry avoid consistently any discussion on the precise definition of point, line, etc. It is our aim to clarify one of notorious question in Euclidean geometry: how many points are there in a line segment? – from discrete-cellular space (DCS) viewpoint. In retrospect, it may offer an alternative of quantum gravity, i.e. by exploring discrete gravitational theories. To elucidate our propositions, in the last section we will discuss some implications of discrete cellular-space model in several areas of interest: (a) cell biology, (b) cellular computing, (c) Maxwell equations, (d) low energy fusion, and (e) cosmology modelling.

Keywords

Discrete-cellular space; Discrete cosmology models; Lattice universe; Cellular automata; Cell biology; Cellular computing

So many students from all ages have asked this question: how many points are there in a line segment? And a good math teacher will answer politely: in the circumference of a circle there are infinite number of points [1]. Similarly one can also ask: how many lines are there in a rectangular? The answer again is known: there are infinite number of lines in given rectangular.

But a careful student will ask again: but what is the definition of point and line? Teacher will answer again: a point is a circle with zero diameter, and line is composed of infinite points.

If our beloved student persists, he/she will continue to ask: but teacher, if a circle has zero diameter, then an infinite number of zeroes will not make a finite line, isn’t it?

At this time, there is fair chance that the teacher feel upset and say: “shut up and calculate!”

That is what usually happens in most primary school mathematics classroom, and the situation is not getting better in undergraduate classroom. Only in graduate math class, then the students are allowed to ask numerous questions, such as foundations of mathematics etc. A more serious debate among mathematicians over this notorious continuum problem has been recorded [2].

Here we will offer a simpler solution of the above posed question from a discrete-cellular space (DCS) viewpoint, with wide implications, including more clarity over distinction between quantization and discretization.

Solution: the space consists of circles with finite diameter (discrete cellular model)

The obvious paradox that we set in the introduction section can be simplified as follows:

0+0+0+….ad infinitum=0

Therefore the basic postulate that a line segment consists of circles with zero diameter is contradictory by itself.

Our proposed solution is to assume that the space consists of circles with small but finite diameter (z), therefore if a line segment consists of circles like that, we have:

z+z+z+…ad infinitum=finite line

One implication of this proposition is that we should better consider the geometry of space not as continuum, but as a discrete-cellular space. And we must remember that discretization of space is much more fundamental than quantization.

Moreover, we can consider the following:

a. It can be shown that similar indeterminacy problem plagues the very definition of differential calculus, as no one knows that actual size of dx [3]:

I turn now to a difficulty which necessarily arises in any attempt to set up an infinitesimal calculus which takes the differential as fundamental concept, namely the indeterminacy of differentials.

The first differential dx of the variable x is infinitely small with respect to x, and it has the same dimension as x. These are the only conditions it has to satisfy, and they do not determine a unique dx, for if dx satisfies the conditions then clearly so do 2dx and ½ dx and in general all adx for finite numbers a. That is, all quantities that have the same dimension and the same order of infinity as dx might serve as dx.

Moreover, there are elements not from this class which satisfy the conditions for dx; for instance dx²|a and √adx, for finite positive a of the same dimension as x. dx²|a is infinitely small with respect to dx and √adx is infinitely large with respect to dx, so that there is even not a privileged class of infinite smallness from which dx has to be choosen; there is no “first” class of infinite smallness adjacemt to finiteness. Thus first-order differentials involve a fundamental indeterminacy.

b. Boyer has shown that Planck blackbody radiation can be derived from discrete charge assumption (without partition as assumed by Planck [4]).

c. Lee Smolin has described three approaches to quantum gravity in his book [5]. But considering our proposition above, it seems that the notion of quantum gravity may be not necessary. Instead, we should consider discrete gravity theories.

d. Gary W. Gibbons and George F.R. Ellis have considered a discrete Newtonian cosmology. That is a good start [5].

e. Gerard ‘t Hooft has proposed a discrete deterministic interpretation of QM [6]. But it seems the use of both discrete and quantum language are superfluous. We need to let go the quantum terminology with its own excess baggage.

f. At astronomical scale, Conrad Ranzan has proposed a cellular universe, which is essectially a Newtonian Steady-State model but with a discrete cellular space model [7]. In our view, such an approach needs to be explored and investigated further. See also our recent paper, where we suggest an ultradiscrete KdV as model of cosmology [8]. Lindquist-Wheeler model [9,10]. We discuss this approach in the last example of last section of this paper.

g. It may be possible for certain conditions, to consider a partially continuum and partially discrete space. In other words, we may have a hybrid space. But we do not investigate it yet.

A bit of philosophical considerations

According to Miguel Lorente, in order to understand better these models it would be useful to consider three levels of human knowledge in the comprehension of the physical world [11]:

Level 1: Physical magnitudes, such as distances, intervals, force, mass, charge, that are given by our sensation and perceptions.

Level 2: Mathematical structures, that are the result of metrical properties given by measurements and numerical relations among them.

Level 3: Fundamental concepts, representing the ontological properties of physical world given by our intelligence in an attempt to know the reality. This level of knowledge is not accepted by some philosophical positions like logical positivismus, conventionalismus, neokantismus.

There must be some connections between the three levels. In QM the theoretical models of microphysics in level 2 are related to observable magnitudes in level 1 by correspondence laws. If we accept level 3 it should be connected to level 2 and to level 1 (through level 2). In fact, the rules governing the constructions of theoretical models in level 2 must be grounded in some fundamental (ontological) properties of the physical world.

It is also worth noting that there are different interpretations of the concepts of space and time. They are usually divided in three classes, as follows [11]:

a. Dualistic theories: Space is a container where the particles and waves are moving. Time is also a separated entity with respect to which the motion takes place. Therefore space and time are absolute and can be thought of in the absence of particles (Newton).

b. Monistic theories: Spacetime is identified with some properties of matter and can not be concevible without the existence of the later. The field of forces and also the sources are nothing more that geometrical deformations of the Spacetime (Einstein, Kaluza-Klein, Wheeler).

c. (c) Relational theories: Spacetime consists of the set of relations among some fundamental objects: monads (Leibniz), units (Penrose), processes (Weisaecker, Finkelstein), preparticles (Bunge, Garc´ıa Sucre), objects (Hilbert).

In the present paper, following our argument in the previous section, we assert that the space consists of discrete cells with finite dimension, which is the most realistic model to the best of our knowledge. Next we will discuss some implications in different areas of interest.

Proof of concept: A few implications of discrete-cellular space

To elucidate our propositions, in this section we will discuss some implications of discrete cellular-space model in several areas of interest: (a) cell biology, (b) cellular computing, (c) Maxwell equations, (d) low energy fusion, and (e) cosmology modelling.

a. Cell biology: The mathematical modeling of cell populations can be, broadly speaking, split into two categories: continuum and discrete models. Discrete models treat cells as individual entities and hence provide a natural framework within which to make use of an increasing amount of experimental data available at the cellular and subcellular scales. There are now many different types of discrete cell-level models used to describe cell populations, e.g., cellular automata, cellular Potts models, cell-vertex, and off-lattice cell based model [12].

While continuum models have their own advantages, they also have certain limitations, as follows [13]: Continuum models of the cell aim at capturing its passive dynamics. In addition to the limitations mentioned above, current models do not yet typically account for active biology: deformations and stresses experienced as a direct consequence of biochemical responses of the cell to mechanical load cannot be predicted by current continuum models. However, by contrasting the predicted purely mechanical cell response to experimental observations, one could isolate phenomena involving active biology, such as cell contraction or migration, from the passive mechanical response of the cell. Alternatively, continuum models might be envisioned that account for active processes through time-dependent properties or residual strains that are linked to biological processes. Another limitation of continuum models stems from lack of description of cytoskeletal fibers. As such, they are not applicable for micromanipulations of the cell with a probe of the same size or smaller than the cytoskeletal mesh (∼0.1–1.0 μm). This includes most AFM experiments. In addition, the continuum models exclude small Brownian motions due to thermal fluctuations of the cytoskeleton, which would correspond to fluctuations of the network nodes in a continuum model and have been shown to play a key role in cell motility (Mogilner and Oster, 1996). Finally, continuum models have so far employed a limited number of time constants to characterize the cell’s behavior. However, cells have recently been shown to exhibit behaviors with power-law rheology implying a continuous spectrum of time scales (Fabry et al., Desprat et al.,). In the meantime, models involving a finite number of time constants consistent with the time scale of the experimental technique can be used, recognizing their limitations [13].

b. Cellular computer: Around 18 years ago, Sipper described a number of interesting features of cellular computer. He began his article by noting that von Neumann‘s architecture—which is based upon the principle of one complex processor that sequentially performs a single complex task at a given moment—has dominated computing technology for the past 50 years. Recently, however, researchers have begun exploring alternative computational systems based on entirely different principles. Although emerging from disparate domains, the work behind these systems shares a common computational philosophy, which can be called as cellular computing [14]. Those cellular computers are supposed to have three principles in common. Combining these three principles results in the definition cellular computing = simplicity + vast parallelism + locality. Because the three principles are highly interrelated, attaining vast parallelism, for example, is facilitated by the cells’ simplicity and local connectivity. Changing any single term in the equation results in a different computational paradigm. So, for example, foregoing the simplicity property results in the distributed computing paradigm. Cellular computing has been placed further along the parallelism axis to emphasize the “vastness” aspect [14]. What specific application areas invite a cellular computing approach? Research has raised several possibilities: [1] Image processing. Applying cellular computers to perform image-processing tasks arises as a natural consequence of their architecture. For example, in a two-dimensional grid, a cell (or group of cells) can correspond to an image pixel, with the machine’s dynamics designed to perform a desired image-processing task. Research has shown that cellular image processors can attain high performance and exhibit fast operation times for several problems. [3] Fast solutions to NP-complete problems. Even if only a few such problems can be dealt with, doing so may still prove highly worthwhile. NP-completeness implies that a large number of hard problems can be efficiently solved, given an efficient solution to any one of them. The list of NP-complete problems includes hundreds of cases from several domains, such as graph theory, network design, logic, program optimization, and scheduling, to mention but a few. [4] Generating long sequences of high-quality random numbers. This capability is of prime import in domains such as computational physics and computational chemistry. Cellular computers may prove a good solution to this problem. [5] Nanoscale calculating machines. Cellular computing’s ability to perform arithmetic operations raises the possibility of implementing rapid calculating machines on an incredibly small scale. These devices could exceed current models’ speed and memory capacity by many orders of magnitude [6]. Novel implementation platforms. Such platforms include reconfigurable digital and analog processors, molecular devices, and nanomachines [14].

c. Maxwell equations: While X.S. Wang [15] was able to derive the above mentioned Maxwell’s equations in vacuum based on a continuum mechanics model of vacuum and a singularity model of electric charges, in the meantime Krasnoholovets has managed to show quite remarkably that the very definition of charge can be modelled from the viewpoint of tessellatice space. He argued that the Maxwell Equations are the manifestation of hidden dynamics of surface fractals [16]. He also concludes that James Clerk Maxwell was right when he involved imaginary cogwheels constructing the equations of motion of the electromagnetic field [16].

d. Low energy fusion: Since the early years of Condensed Matter Nuclear Science (aka. LENR/Cold fusion), Robert W. Bussard from Energy/Matter Conversion Corporation has argued in favor of internal nuclear fusion in metal lattice to explain the low energy reaction as reported by Pons and Fleischmann [17]. Subsequently, there are a number of researchers who have explored the implications of lattice vibration and lattice structure models from solid state physics in order to explain CMNS process. Such approaches seem to be quite promising and they are worthy to continue further [18-20]. For a recent discussion on discrete and continuum modelling, see for instance [21].

e. Cosmology modeling: Many physicists and philosophers alike have debated a long standing puzzle: whether the space is continuous or discrete. It has been known for long time that most of the existing cosmology models rely on pseudo-Riemannian metric as the cornerstone of Einsteinian universe. But the metric itself is based on continuum theory. It is known that such models have led us to too many (monster) problems, including dark matter and dark energy etc. Now what if the universe is discrete? Then perhaps we can solve these problems naturally. Philosophically speaking, the notion of discrete space can be regarded as basic question in definition of differential calculus and limit. If it is supposed that space is continuous then we can use standard differential calculus, but if we assume it is finite and discrete, then we should use difference equation or finite difference theories. This problem is particularly acute when we want to compute our mathematical models in computers, because all computers are based on discrete mathematics. Then we can ask: is it possible that the discrete mathematics can inspire cosmology theorizing too? Despite majority of cosmologists rely on such a Standard Model which is called Lambda CDM theory, we will explore here the redshift theory based on a few of lattice-cellular models, including Lindquist-Wheeler theory and beyond it. We will also touch briefly some peculiar models such as Voronoi tessellattice and also Conrad Ranzan’s cellular model of the Universe.

a. Lindquist-Wheeler’s theory: In this model, the matter content is assumed to be discrete; identical spherically symmetric islands uniformly distributed in a regular lattice. This attempt was first introduced in 1957 by Lindquist and Wheeler (LW) in a seminal paper. While LW suggested that their global dynamics is similar to Friedmann universe for closed dust dominated universe, Shalaby has shown that LW-model can be extended to yield a redshift equation, as follows: [9]

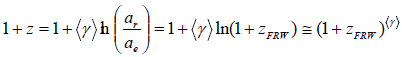[1]

It can be shown, that the value of ⧼γ⧽ approximates geometrically to be 2/3, however, numerically its value was estimated to be 7/10. Liu [22] also analyzed LW model, and he concludes that the LW redshifts can differ from their FLRW counterparts by as much as 30%, even though they increase linearly with FLRW redshifts, and they exhibit a non-zero integrated Sachs-Wolfe effect, something which would not be possible in matter-dominated FLRW universes without cosmological constant [10].

b. Voronoi Tessellation model: Rien van de Weygaert describes a novel model based on Voronoi tessellation. The spatial cosmic matter distribution on scales of a few up to more than a hundred Megaparsec displays a salient and pervasive foam-like pattern [23]. Voronoi tessellations are a versatile and flexible mathematical model for such weblike spatial patterns. Cellular patterns may be the source of an intrinsic geometrically biased clustering. However, so far we do not find a redshift equation from this model [24].

c. Non-expanding cellular universe: Conrad Ranzan [25] suggests a DSSU cellular cosmology (dynamics steady state universe), which he claims to be problem-free. The cosmic redshift is shown to be a velocity-differential effect caused by a flow differential of the space medium. He obtains the cosmic redshift equation in its basic form [8]:

[2]

There are of course other cellular cosmology models, some of them have been reviewed by Marmet, but this paper is not intended for such an exhaustive list of redshift models [26].

Concluding remarks

An old question and paradox in Euclidean geometry may be resolved consistently, once we accept and assume a discrete space instead of continuum model which is full of indeterminacies [27].

Many implications and further developments can be expected both in particle physics realm and also in cosmology theorizing. More observation and experiments are recommended to verify whether the space is discrete, continuous, or hybrid.

In retrospect, it may offer an alternative of quantum gravity, i.e. by exploring discrete gravitational theories. To elucidate our propositions, in the last section we discuss some implications of discrete cellular-space model in several areas of interest: (a) cell biology, (b) cellular computing, (c) Maxwell equations, (d) low energy fusion, and (e) cosmology modelling.

Acknowledgement

The first author (VC) would like to thank to participants of 3^rd Conference on Theoretical Physics and Nonlinear Phenomena, held in Bandung at 1^st August 2017, whose discussions have inspired this paper. And special thanks to Prof. (Em.) Thee Houw Liong from Bandung Institute of Technology (ITB) for encouraging advises, and also to anonymous reviewer for suggesting improvement of this paper. We also gratefully appreciate Dr. Volodymyr Krasnoholovets for sending his new book describing tessellation model of space and its physical implications.

REFERENCES

1. https://math.stackexchange.com/questions/1799125/how-many-points-in-a-line-segment
2. https://www.ias.edu/ideas/2011/kennedy-continuum-hypothesis
3. Bos HJ. Differentials, higher-order differentials and the derivative in the Leibnizian calculus. Archive for History of Exact Sci. 1974;14:1-90.
4. Boyer TH. Connecting blackbody radiation, relativity, and discrete charge in classical electrodynamics. Foundations of Physics. 2007;37:999-1026.
5. Smolin L. Three roads to quantum gravity. Basic books, 2008.
6. Ellis G, Gibbons G. Discrete Newtonian Cosmology. Classical and Quantum Gravity. 2013;31:025003.
7. Gerard ‘t H. A Deterministic Interpretation of Quantum Mechanics Fundamental Theories of Physics 2016; 185.
8. Ranzan C. The Large Scale Structure of the Dynamic Steady State Universe. Am J Astronomy and Astrophysics. 2016;4:65-77.
9. Christianto V, Smarandache F, Umniyati Y. An Outline of Cellular Automaton Universe via Cosmological KdV Equation. Prespacetime J. 2017;8:1-24.
10. Shalaby M. Dynamics and Light Propagation in a Universe with Discrete Matter Content. arXiv preprint arXiv:1205.6877. 2012.
11. Liu RG. Lindquist-Wheeler formulation of lattice universes. Physical Review D. 2015;92:063529.
12. Miguel L. A realistic interpretation of lattice gauge theories. 2003.
13. Murray PJ, Edwards CM, Tindall MJ, et al. From a discrete to a continuum model of cell dynamics in one dimension. Physical Review E. 2009;80:031912.
14. Mofrad MR, Karcher H, Kamm RD. Continuum elastic or viscoelastic models for the cell. 2006;21:29.
15. Sipper M. The emergence of cellular computing. Computer. 1999;32:18-26.
16. Wang XS. Derivation of Coulomb's Law of Forces Between Static Electric Charges Based on Spherical Source and Sink Models of Particles. arXiv preprint physics/0609099. 2006.
17. Krasnoholovets V. Structure of Space and the Submicroscopic Deterministic Concept of Physics. CRC Press. 2017;118:145.
18. Bussard RW. Virtual-state internal nuclear fusion in metal lattices. Fusion Technology. 1989;16:231-6.
19. Steven E. Jones, Palmer EP, Czirr JB, et al. Observations of Cold Nuclear Fusion in Condensed Matter. Nature 1989;338:737-40.
20. Fleischmann M, Pons S, Hawkins M. Electrochemically induced nuclear fusion of deuterium. J Electroanalytical Chem. 1989;261:301-8.
21. Arata Y, Zhang YC. Formation of condensed metallic deuterium lattice and nuclear fusion. Proceedings of the Japan Academy, Series B. 2002;78:57-62.
22. Kuzkin VA, Krivtsov AM, Podolskaya EA, et al. Lattice with vacancies: elastic fields and effective properties in frameworks of discrete and continuum models. Philosophical Magazine. 2016;96:1538-55.
23. Kirillov AA, Turaev D. Foam-like structure of the Universe. Physics Letters B. 2007; 656 1-8.
24. Van De Weygaert R. Voronoi tessellations and the cosmic web: Spatial patterns and clustering across the universe. InVoronoi Diagrams in Science and Engineering, 2007. ISVD'07. 4th International Symposium on 2007;230-239.
25. Conrad R. Large scale structure of the Dynamic Steady State Universe. Am J Astronomy and Astrophysics. 2016;4:65-77.
26. Louis Marmet. On the Interpretation of Red-Shifts: A Quantitative Comparison of Red-Shift. 2013.
27. Conrad R. Cosmic redshift in the non-expanding cellular universe: velocity-differential theory of cosmic redshift. Am J Astronomy and Astrophysics 2014;2:47-60.