Pre-service and In-service primary teachers' generic and subject-specific skills on Geometric understanding of symmetry: A case study

Shiva Mafakheri

doi:10.37532/2752-8081.22.6.3.1-3

Shiva Mafakheri^*

Science department, Farhangian University, Kurdistan, Iran, Email: sh.mafakher@gmail.com

^*Correspondence: Shiva Mafakheri, Science department, Farhangian University, Kurdistan, Iran, Tel: +00989188729856, Email: sh.mafakher@gmail.com

Received: 10-Mar-2022, Manuscript No. puljpam-22-4458; Editor assigned: 14-Mar-2022, Pre QC No. puljpam-22-4458(PQ); Accepted Date: Apr 29, 2022; Reviewed: 07-Apr-2022 QC No. puljpam-22-4458(Q); Revised: 21-Apr-2022, Manuscript No. puljpam-22-4458(R); Published: 04-May-2022, DOI: 10.37532/2752-8081.22.6.3.1-3

Citation: Mafakheri S.Pre-service and In-service primary teacher's generic and subject-specific skills on Geometric understanding of symmetry: A case study. J Pure Appl Math.2022;6(3):1-3

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

According to the curricula all over the world symmetry plays an important role in the teaching geometry at primary levels. Geometry is one of topics that have the most problematic content knowledge for the prospective primary teachers. This paper studies the understanding of the symmetry of shapes among pre-service and in-service teachers to find out their visual perception of the geometric shapes symmetry and the symmetry axis. The aim is to create a symmetrical pattern with symmetry axis of the shapes. Evidence that only content-oriented professional development coursework taken by primary school math teachers appears effective, suggests that relatively more resources ought to be put into content focused training for teachers and that changes are warranted at the elementary level and in pedagogical in-service training generally. The primary teacher needs to be able to modify some proposed problems in order to get a richer mathematical activity, being aware of their mathematical benefits. It should be part of growing the capacity of analyzing didactically the mathematics activity.

Key Words

Pre-service teachers; in-service teacher; mathematics education, symmetry; symmetry axis

Introduction

Teaching geometry is in fact translations, rotations and reflections but oriented towards drawing and the recognitions of basic plane figures. Therefore primary pre-service teachers need a lot of activities about geometrical transformation during their education [1].

Reform documents such as The Curriculum and Evaluation Standards for School Mathematics (NCTM, 1989), Principles and Standards for School Mathematics (NCTM, 2000) describe the best practices of highquality mathematics instruction[2,3]. Many teacher education programs have integrated research-based reforms suggested by these documents into their curriculums. According to the Iran curriculum for primary level, mathematics is an abstract system, which must be presented to the children via concrete manipulative activities creating basic concepts of mathematics about: numbers, counting, size, shapes, quality of objects and their place in space and time[4]. The main goal of curriculum is creating thinking, modeling, space orientation, geometry, probity and problem solving. A problem is how to articulate theoretical notions of onto semiotic perspective of constructing mathematical objects and processes with problem posing in teacher training courses in order to produce good mathematical and didactical problems promoting professional development.

As a result, primary education in Iran holds more importance. The main aim of learning mathematics in primary school is for the pupil of acquire the knowledge that they will need for development of their skills in the course of further education and daily life [5].

Nowadays the educational software’s have an important role in learning symmetry. Another important role of symmetry is about manipulative verification of equivalence in the primary school textbooks [6].

This paper shows a descriptive study of pre-service and in-service teacher’s ability for symmetry. Symmetry patterns are varying in Persians’ art as carpet patterns, tile templates. Children have more experiences in their real-life activities. Symmetry in Iran’s curriculum is an important part of mathematics education at primary level. Farhangian University in Kurdistan, Iran prepares future primary teachers. Most of student has no positive approach to mathematics and geometry particular, while they are going to teach math in primary school.

Students of primary teacher training are mostly having only small number of hours dedicated to teaching mathematics in their curriculum. Part of them graduated of high school on mathematics field, yet most of them were at other fields with less mathematics ability [7].

For this reason, they have a lesser understanding of mathematics notions and aren’t then taking a compulsory course in geometry with didaction as a part of their university study program [8]. Research reveals that the most problematic content knowledge for the prospective elementary teachers is geometry [9].

The aim of this is to answer the question that “How good pre-service and in-service teachers in knowing and finding are construct symmetry in patterns?”

Method

Participants

Pre-service teachers bring perspectives of, and beliefs about, mathematics teaching from their own schooling and are presented with opportunities to refine their perspectives as they progress through teacher preparation programs. Many in-service teachers have had additional opportunities to refine their perspectives with classroom experience along with textbooks, curriculum documents, and professional development activities.

Examining the differences in perspectives in practice, held by pre-service and in-service teachers might reveal which perspectives of high-quality mathematics instruction need further support. Therefore, sample was selected from both of them. 103 Pre-service primary teachers of Kurdistan Farhangian University take part in this study and 20 in-service primary teachers that have more than 15 years’ experience of teaching elementary school mathematics.

Measuring Tool

Teacher’s knowledge can be established from the analysis and description of the activities needed to plan, manage and evaluate a mathematics lesson. Thus, the problem of the teacher’s knowledge can be considered as the integration of knowledge, abilities and attitudes for action.

Instead of thinking on what the teacher should know, what they should be able to do in a specific context of students’ learning is important. Therefore, Participants were given a practical task on symmetry.

This task was chosen from textbook, Training of Teacher students By J.L.Martin [10].

They have the same time for thinking and doing this task. This task is part of their activity of their University mathematics course [11].

Task

Axis of symmetry is a line that divides an object into two equal halves, thereby creating a mirror-like reflection of either side of the object.

The word symmetry implies balance[12]. Symmetry can be applied to various contexts and situations. Symmetry is a key concept in geometry which cuts the figure into two halves that are exact reflections of each other, as shown in the figure given below

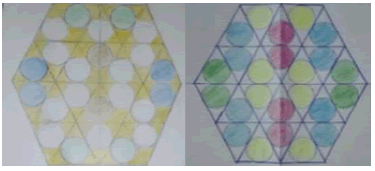
1. Draw a regular hexagon and explain the way that you used.

2. After drawing the sides and diameters, connect the middle of sides, till obtained 24 equal triangles in figure 1.

Figure 1: 24 Equal Triangles in hexagon shape.

3. Draw the circurnference of each triangle, as shown in the figure 2.

Figure 2: Paint all triangles according just following patterns.

Find the symmetry axis of the shape. Then paint another shape that has 1 or more symmetry axis, try another way just with the above paint patterns.

Result and Discussion

Overview and Qualitative results for the task

Most of participants can draw the regular hexagon shape by using enclosing circle. In the diagnosis of color patterns some of them have difficulties. Horizontal or vertical axis of symmetry in the shape is not according expectations of them. The data in table 1 shows that there are some students who identify incorrect axis.

TABLE1 Frequency& percentage of results for pre-service teachers

		Frequency(N=103)	Percent%
Correct drawing		89	86.4
Correct painting (follow pattern)		63	61.2
	1	63	61.2
Find symmetry axis	2	42	40.3
	3	36	35
	More	21	20.3

Most of the pre-service teachers, as it shows in table1, have a weak knowledge about symmetry axis. They use their own schooling geometry and are presented with opportunities to refine it through teacher preparation programs in university.

According to table 2, most of in-service teachers don’t be able to do correctly. It shows that their teaching experiences just help them in the drawing the shapes, and it’s not enough to solve the task.

TABLE2 Frequency& percentage of results for in-service teachers

		Frequency(N=103)	Percent%
Correct drawing		20	100
Correct painting(follow pattern)		12	60
	1	11	55
Find symmetry axis	2	7	35
	3	5	25
	More	2	10

Then the results were measured with a chi-square test to compare the results of both of them. A chi-square (χ² ) statistic is a measure of the difference between the observed and expected frequencies of the outcomes of a set of events or variables. χ² depends on the size of the difference between actual and observed values, the degrees of freedom, and the samples size. χ² can be used to test whether two variables are related or independent from one another or to test the goodness-of-fit between an observed distribution and a theoretical distribution of frequencies.

The results of the Chi-square test for comparing the correct answers of pre-service and in-service teachers are presented in Table 3. For each of the 6 sections of the task presented to the subjects, in columns 3 and 5, the number of correct answers and columns 4 and 6, the number of incorrect answers in each group can be seen. There was no significant difference between the two groups in drawing the correct shape (χ2 (1)=3.07, P>0.05). The performance of the two groups of teachers in coloring was not different (χ² (1) = 0.01, P> 0.05). There was no difference between the teachers in the four Chi-square tests related to the axis of symmetry (P>0.05).

TABLE3 Chi-Square test of results

		Pre-service		In-service
		correct	Wrong	correct	wrong	df	Chi-Square
Correct Drawing		89	14	20	0	1	3.07ns
Painting(follow pattern)		63	40	12	8	1	0.01 ns
Find symmetric axis	1	63	40	11	9	1	0.27 ns
	2	42	61	7	13	1	0.23 ns
	3	36	67	5	15	1	0.75 ns
	more	21	82	2	18	1	1.19 ns

Overview and qualitative results for the task

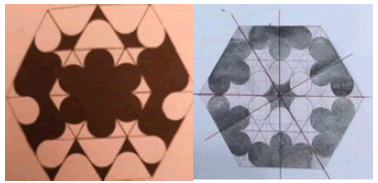
The results were qualitatively classified into four types, which named codes. These categories were examined in the total answers and the type of response of the participants, regardless of their category (pre-service or in-service). Based on the detection of staining and the correct measurement of the axis of symmetry, these categories were defined in figure 3-6. Following the patterns and finding the right answer and complete conclusion were the main materials of these categories.

Figure 3: Participants donâ??t understand the template patterns for painting; therefore have misunderstanding on doing task. Most of in-service teachers did in this way. It shows that Experience alone is not enough for teaching the concepts.

Figure 4: They understand patterns and do it in correct way, yet finding the symmetry axis shows that they donâ??t have correct idea about it. In this code both of two groups of participants exist.

Figure 5: Most of pre-service teachers that take part in this study imagine that there is just horizontal and vertical symmetry axis.

Figure 6: They found a correct and deep understanding and perspective about the task and did their homework in the best way.

Code 1

Losing the pattern and don’t understand what symmetry is in shape, most of them don’t know how can follow the painting patterns.

Code 2

Participants who follow the painting pattern in correct way but can’t develop finding right numbers symmetry axis.

Code 3

Participants who follow the painting pattern in correct way and develop finding right symmetry axis just in horizontal and vertical.

Code 4

They do it in correct way. The correct painting followed and specified axis in right way.

Conclusion

The mathematization of ordinary human ideas is an ordinary human enterprise. This is possible because concepts like change, proportion, size, symmetry, rotation and hundreds of others are both everyday ideas and ideas that have been mathematicized.

In this research, the effects of teacher training have been unable to overcome challenges in estimating the effects of training on teacher quality. When no significant differences are found in the results, the conclusion is that education or experience alone is not enough, but a correct and in-depth perspective about the content is necessary.

The goal of this research is to create a symmetrical pattern, not just to find the symmetry axis of the shapes, which need for a deep understanding of the concept of symmetry and symmetry axis in any shape. In both preservice and in-service teachers, it was observed that the results of the task are not effective on the personal teaching experience and the emphasis on content is more fundamental in the concept of symmetry. It is difficult to isolate productivity, especially in teaching where a teacher’s own ability, the influences of other characteristics also affects measured outcomes. There is an inherent selection problem in evaluating the effects of education and Training on teacher productivity.

It is difficult to obtain data that provide much detail about the various types of training teachers receive and even more difficult to link the training of teachers to the achievement of the students they teach.