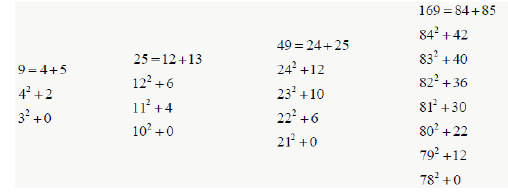Prime numbers

Received: 02-Dec-2023, Manuscript No. puljpam-23-6878; Editor assigned: 03-Jan-2024, Pre QC No. puljpam-23-6878 (PQ); Accepted Date: Mar 27, 2024; Reviewed: 15-Jan-2024 QC No. puljpam-23-6878 (Q); Revised: 31-Jan-2024, Manuscript No. puljpam-23-6878 (R); Published: 31-Mar-2024, DOI: 10.37532/27528081.24.8(2).01-02

Citation: Saadi AA. Prime numbers. J Pure Appl Math. 2024; 8(2): 01-02.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

Prime numbers, the building blocks of arithmetic, have fascinated mathematicians for centuries due to their unique properties and elusive nature. This abstract delves into the captivating realm of prime numbers, presenting an overview of their significance, characteristics, and mathematical properties. We explore the fundamental definition of prime numbers as integers greater than one, possessing only two positive divisors: one and themselves. From the ancient Greeks to modern mathematicians, prime numbers have remained a subject of intense study, with their distribution, patterns, and unpredictability continuing to intrigue and challenge researchers. Through various theorems, conjectures, and mathematical proofs, mathematicians have unveiled numerous mysteries surrounding prime numbers, yet many questions remain unanswered, fueling ongoing research and exploration. Additionally, prime numbers play a crucial role in cryptography, number theory, and various fields of science and technology, underscoring their practical importance beyond pure mathematics. This abstract provides a glimpse into the captivating world of prime numbers, inviting further exploration and inquiry into one of mathematics' most enduring puzzles.

Key Words

Prime numbers; Economic growth; Causality; Vector error correction model; Positive divisors

Introduction

In this work consists of showing whether a number is prime, or not. Let’s take examples to explain this:

Example 1: the number 17, we write this number as the sum of two consecutive numbers, one even, the other odd: 37=18+19

Note 1: in this sum, the even number 18 is smaller than the odd number which is 19.

We proceed as follows: we divide our work in two columns C₁ and C₂

In the column C₁ we form a decreasing arithmetic sequence of reason 1, its terms we square them

In the column C₂ we form a descreasing sequence of reason -2n.

37=18+19, we divide the even number 18 by 2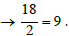

C₁ and C₂

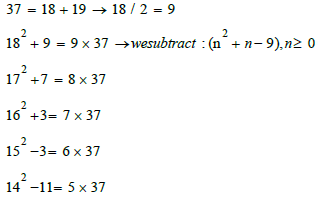
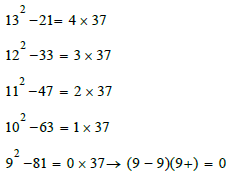
So the number 37 is prime because we find the form: a² - b² = 0

Note(A): In the first line we have: 18² + 9 = 9 × 37; in the last line we have 9² - 81. We have the number 9 at the beginning and at the end

Example 2: The number 59. We write this number as the sum of two consecutive numbers. One even and the other odd

59 = 29 + 30

Note 2: in this example the even number (30) is greater than the odd number (29). We proceed as follows: we divide our work into columns C₁ and C₂.

In the column C₁ we form a decreasing arithmetic sequence of reason 1.Its terms we square them.

In the column C₂. we form a decreasing sequence of reason -2n

C₁ and C₂

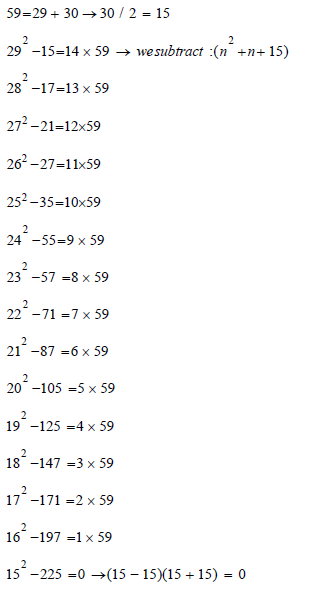
Note(B): in the first line we have: 292 - 15 = -14 × 59; in the last line we have 15² - 225. we have the number 15 at the beginning and at the end.

So the number 59 is prime because we find the form a² - b² = 0

If the number is prime then impossible to find: a² - b² ≠ 0

But if we then find a² - b² ≠ 0 the number is not prime.

Note 4: for the 1st example (number 37=18+19) we added between 18² and 9

18² + 0 = 9 × 37

Because the even number 18 is smaller than the odd number 19.

For the second example (number 59=29+30) we subtract between 29² and 15, 29² - 15 = 14 × 59

Example 3: in this case the even number 26 is greater than the odd number 25.

We proceed as in example 2.

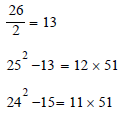
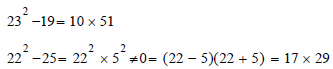
So 51 is not prime number, it is a multiple of 17, and a² - b² ≠ 0

Example 4: 91=45+46; in this case even number 26 is greater than the odd number 25. We proceed as in example 2.

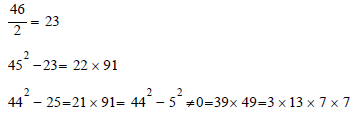
So 91 is not prime, because it is in the form a² - b²≠ 0

91 = 7 × 13 Values that we find in our calculation

Example 5: 21=10+11

10² + 5 = 5×21

9² + 3 = 4 × 21 So 21 is not prime number

8² - 1 = 8² - 1² = 3 × 21 = (8-1)(8+1) = 7 × 9

Note 5: if the number is a perfect square, then we find: a² + 0 (Figure1).

Figure 1: Perfect square