Program to calculate the 15 first mersenne’s primes numbers and further perharps

Received: 02-Apr-2024, Manuscript No. puljpam-24-7044; Editor assigned: 06-Apr-2024, Pre QC No. puljpam-24-7044(PQ); Accepted Date: May 29, 2024; Reviewed: 25-Apr-2024 QC No. puljpam-24-7044(Q); Revised: 30-Apr-2024, Manuscript No. puljpam-24-7044(R); Published: 31-May-2024, DOI: 10.37532/2752- 8081.24.8(3).01-02

Citation: Strainchamps D. Program to calculate the 15 first mersenne’s primes numbers and further perharps. J Pure Appl Math. 2024; 8(3):01-02.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

This article present an algorythm to calculate the 15 first Mersenne’s Primes Numbers with the knwoledge of the 2 first 3 and 5.

Key Words

Mersenne; Primes; Algorithm

Introduction

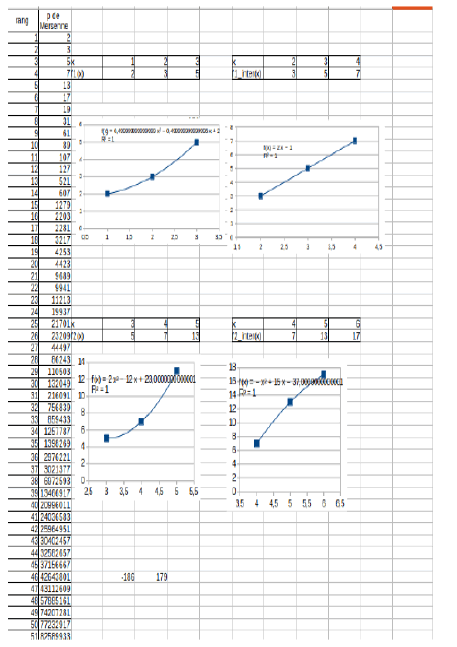
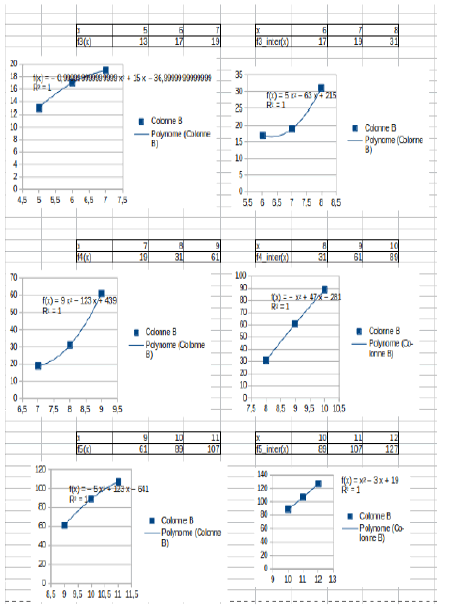
First I see second degree polynomial structure and second I see: if you know the coeffecient a of the second degree polynom you can calculate the future prime’s Mersenne (Figures 1 and 2).

Figure 1: Polynomial structure

Figure 2: Second polynomial structure

Second I see: If you know the coeffecient a of the second degree polynom you can calculate the future prime’s Mersenne

Theorem 1: If a= 2 * [0, 2, -1, -1, 5, 9, -1, -5, 1, 187, -154, 293, 126, -423, 429, 50, -433, 2548, -2507, 510, 3726, -3480, -128, 9890, 10229, -8740, -1357, 31248, 228353, - 219077, 147880, -128936, 718735, -766398, 1953030, 1271554, 517385, -2244261, -556102, 1254569, -1128653, 1196905, 456562, -2509163, 7151872, 774784, -6648242, 1165690] then m[i+2] = a + 2 * m[i + 1] - m[i] with M[1] = 3 and M[2]= 5

Proof. Proofed with an algorithm and the verification that all 51 known Mersenne’s Primes are found.

Algorithm to find the 15 first Mersenne’s primes numbers

the script is here

Conclusion

This algorithm allow to find the 15 first Mersenne’s primes but is limited by the condition

gmpy2.is_prime(mpz(’2’)** abs(m3)-1)

It will be for further research interesting to replace this condition by a Lucas Lehmer test.