Sigmoid functionization of magnetization in the spin-glass Ising model.
Received: 16-May-2024, Manuscript No. puljpam-24-7053; Editor assigned: 17-May-2024, Pre QC No. puljpam-24-7053 ; Accepted Date: May 27, 2024; Reviewed: 19-May-2024 QC No. puljpam-24-7053; Revised: 20-May-2024, Manuscript No. puljpam-24-7053; Published: 31-May-2024, DOI: 10.37532/2752- 8081.24.8(3).01-02
Citation: Saito A. Sigmoid functionization of magnetization in the spinglass Ising model. J Pure Appl Math. 2024; 8(3):01-02.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
The magnetization of the spin-glass Ising model can be expressed using a sigmoid function. In the ground state, the magnetization is determined by solving a set of nonlinear simultaneous equations, each corresponding to a magnetization. As the magnetization of the ground state in the spin-glass Ising model constitutes an NPcomplete problem, the P=NP problem can be reformulated as solving these nonlinear simultaneous equations. If practical computation yields result that are feasible, it can be essentially considered as P=NP. Furthermore, all interacting systems in nature can be represented by sigmoid functions, and the ground state can be obtained by solving nonlinear simultaneous equations.
Key Words
Sigmoid function; Interacting systems; Ground state; Practical computation; Magnetization
Introduction
The Ising model is the simplest and most fundamental interactionmodel. Each spin (node) interacts with each other, taking states of either -1 or 1, and evolves continuously at temperature T, eventually converging to a state called the ground state at T=0. This ground state has the lowest energy in the system, with each state's expected value being the order parameter taking -1 or 1. It represents how the system settles due to interactions. In complex systems, the resultant states of interactions serve as solutions to combinatorial optimization problems (NP problems). In the real world, solutions to interaction systems and combinatorial optimization problems have wide applications across various fields. The spin-glass Ising model is a variant of the Ising model where interactions include both positive and negative components individually. It can model various interaction systems and combinatorial optimization problems. Now, the magnetization of this spin-glass Ising model has been represented using a sigmoid function. Furthermore, in the ground state, magnetization can be expressed by a set of nonlinear simultaneous equations for each magnetization. Combinatorial optimization problems (NP problems) and interacting systems can be reduced to solving these nonlinear simultaneous equations. Below, we present the derivation of these equations.
Results
At all temperatures, the following results were obtained.
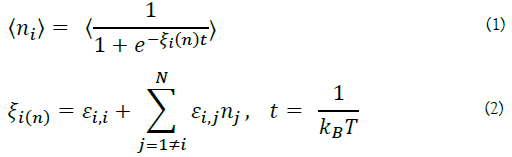
Also, at the ground state (T=0), the following results were obtained.
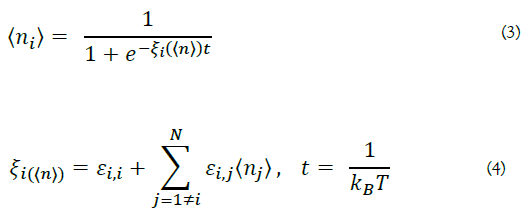
Theory
Let there be state variables for each node i = 1 to N, each with the following states.

The model, represented by the following Hamiltonian of the system, is called the Ising model [1]. (Although the Ising model is generally characterized by n = -1 or 1, it can be simplified for calculations as n = 0 or 1.)

However, εij can take any value within the specified range (spin-glass Ising model) [2].

The order parameter <ni> is determined by the following.
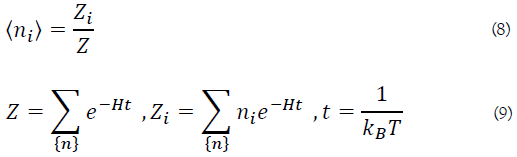
From equations (5), (8) and (9)
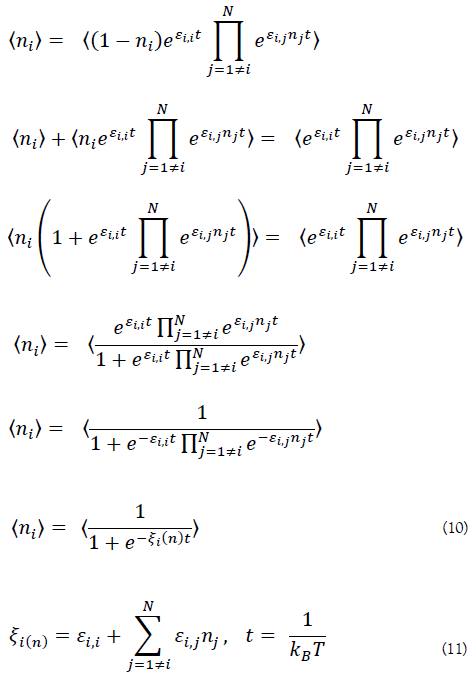
Based on the above, equations (1) and (2) are obtained. Equation (10) (equivalent to equation (1)) is a sigmoid function.
Furthermore, at t=∞, From <n>=0 or 1
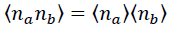
From the above, using the relations in equation (10)'s expansion, equations (11) and (12) are obtained.

This constitutes a set of nonlinear simultaneous equations for <ni>. In other words, the problem of finding the order parameters <ni> of the ground state reduces to solving these nonlinear simultaneous equations.
Discussion
In mathematics, there exists an unresolved problem known as the P vs NP problem. This problem, in the field of computer science, raises the question of whether if a solution to a problem can be efficiently verified, can it also be efficiently found? Here, "efficiently" means that the solution can be computed in polynomial time with respect to the size of the problem. "Polynomial time" refers to an algorithm that takes time proportional to n raised to a constant power (where n is the size of the problem). In essence, the P vs NP problem asks whether all problems for which solutions can be quickly verified (NP) are also problems for which solutions can be quickly found (P). Now, about this problem, the ground state of the spin-glass Ising model has been reduced to a solution of a set of nonlinear simultaneous equations. Since finding the ground state of the spin-glass Ising model is equivalent to NP-complete problems, which can be converted to all NP problems, if the solution to these nonlinear simultaneous equations can be obtained through numerical computation, it can be said that P=NP within a practical range.






