The effect of selection of initial values on finding the root of a multiple roots–polynomial equation
Received: 22-Sep-2022, Manuscript No. PULJPAM-22-5392; Editor assigned: 26-Sep-2022, Pre QC No. PULJPAM-22-5392 (PQ); Accepted Date: Mar 27, 2023; Reviewed: 10-Oct-2022 QC No. PULJPAM-22-5392; Revised: 20-Feb-2023, Manuscript No. PULJPAM-22-5392 (R); Published: 31-Mar-2023, DOI: 10.37532/2572-8081.23.7(2).1-7
Citation: Batarius P. The effect of selection of initial values on finding the root of a multiple rootsâ??polynomial equation. J Pure Appl Math 2023;7(2):1-7.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
This study aims to determine the effect of selecting the initial value on the root of a polynomial equation that has multiple roots. There are three methods used, namely the Brent method, the bisection method and the modified secant method. The Brent method is a combination of the bisection method, the IQI (Interval Quadratic Inverse) method and the secant method. Therefore, it is necessary to know the performance of the Brent method in finding the multiple roots of polynomial equations. The search for multiple roots reaches convergence faster when using the modified Newton-Raphson method or the modified secant method. There are 2 types of polynomial equations used. One equation has 3 roots and two of them have multiple roots (multiple roots). One other equation is a polynomial which has 4 equal roots and 3 of them have multiple roots with an odd number of roots. The analysis was carried out by selecting the same initial value for the three methods. The same lower bound is a=xl=xi-1 for the Brent method, the modified bisection method and the modified secant method, respectively. Likewise for the upper bound a=xu=xi. The selection of the initial value affects the final result of the root search, for the Brent method, the bisection method and the modified secant method. The comparisons made refer to the results of the root value and the speed of convergence as seen from the number of iterations of each method. From the simulation results, we propose the use of a modified secant method because it is more efficient in finding multiple roots in polynomial equations. For the Brent method, it needs to be further modified in order to get the multiple root value in the polynomial equation.
Keywords
Polynomial; Brent method; Bisection method; Modified secant method; Root finding
Introduction
The root of f(x)=0 is the value of x that satisfies the equation, where f(x) is a function of x. The form of the function can be varied, such as polynomial, exponential or a combination of two or more forms of equations. The form of these equations is not only found in mathematics, but also in other engineering fields.
We know that many methods are used to find the roots of an equation that make the function zero. Some of the basic methods used, based on the selected initial guess, include the bisection method and the wrong position method (which are included in the closed method). In addition, there are also open methods such as the Newton-Raphson method and the secant method. The closed method always succeeds in finding the root because it has enclosed the root first, but the convergence process is very slow. Unlike the open method, there is no need to enclose the root in the initial guess.
Various methods have been developed to find the root of the equation of a function f(x). This development intends to be more efficient in the root search process. The measurement of the efficiency of a method is characterized by the number of iterations used less, the resulting error value close to zero and faster convergence. Like the hybrid algorithm between the bisection method and the Newton-Raphson method, convergence is faster in finding the roots of non-linear equations [1].
The hybrid algorithm process between the bisection method and the modified Newton-Raphson method, converges faster on the nth positive real root search. The root search process is influenced by the initial value given. Initial values need to be considered in finding the real roots of an equation [2]
The secant method is the most effective method of the bisection method, and the Newton Raphson method with the function used is f(x)=x-cos x. The secant method has a level of convergence that is close to the Newton- Raphson method, but only requires the evaluation of a single function per iteration [3].
The secant method has the fewest iterations to get the optimal Photovoltaics (PV) parameter value compared to the bisection method. This numerical solution was obtained in the research applied to the non-linear function of a PV cell that has one diode. The bisection method and the secant method were applied, with the result that the secant method was more efficient and more accurate [4].
The search for the simple roots of non-linear equations is to apply a new approximation correction technique to the second and third order Taylor series to obtain an iterative method. This correction technique does not affect the number of functional evaluations but on the convergence [5]. Iterative schemes are also used in finding the multiple roots of non-linear equations. The computation time is less with the iterative scheme in finding multiple roots, because of the consistent convergence [6].
Implementation of several methods such as the secant method is used to calculate the optimal path length of the microwave from point to point. The secant method is quite stable in the calculation process even in rainy weather conditions [7]. In addition to the secant method with two initial guesses, the development of the secant method also uses one initial guess. The results converge faster in computing than the conventional secant method [8].
One method that is widely used today in various fields of science is the Brent method. The Brent method is a combination or hybrid of several methods, both closed and open methods. The Brent method is a combination of 3 methods. Sometimes called the Brent-Dekker method. The three methods are the bisection method, the secant method and the IQI (Interval Quadratic Inverse) method. The implementation of the Brent method includes calculating the approximate value of Rs precisely at every fine-tuned point n. As a result the related parameter once the estimate of Rs is known, all other parameters can be determined. The proposed Brent method outperforms some of the computations proposed to mine the parameters of a single diode model for solar cells [9].
The Brent-Dekker algorithm is also used to facilitate real-time deflection control in the Computer Numeric Control (CNC) kernel by sampling and filtering the cutting force signal. This method is applied to the control of cutting deflection in milling blade sections, real time strategic control of feed rate scheduling in a modular CNC architectural system [10].
Although the Brent method combines 3 methods, it needs modification. The results of these modifications are applied to several forms of equations to find the roots of these equations. In addition, it is also applied to several other application fields. In finding the root of the equation, for example, the Brent method is modified by replacing the secant method with the wrong position method. The Brent-Deker method is a combination of the wrong position method, the IQI and the bisection method. The performance of this modified method is better than the Brent-Dekker method, seen from the execution time on several types of equations being tested [11]. The Brent method is also modified in solving the type-3 fuzzy polynomial interval problem. The Brent method is used to find the roots of the previously modified polynomial. The modified Brent method shows that the number of iterations is smaller than the regular Brent method. The resulting error is also smaller and computationally shorter in getting the solution [12].
The Brent method was also improved to control the bridge balance system. These improvements correct the weaknesses of the traditional Brent method. The results show a more stable accuracy with a higher response speed. The bisection method in the Brent method can only be used in real numbers and cannot be used in the domain of complex numbers. The Brent method is modified by an iterative method with extrapolation [13].
Linear Multi Method (LMM) based root search has convergence value that does not exceed the number of +2 derivatives. The Brent method in terms of efficiency is preferred even though the index value is still higher. However, based on the value of convergence, the LMM based method is a better choice [14].
One of the methods used in the Brent method is the Secant method. The secant method itself has been modified in several studies for various implementations. Among them, the modified secant method proposed by Babaie-Kafaki et al, is used in a new approach to the spectral conjugate gradient method in infinite optimization. The new method is more efficient than the classical conjugate gradient method [15]. The modified secant method is also used to achieve higher order accuracy in approaching approximation errors with high accuracy. The use of the modified secant method is more efficient and significantly computationally efficient in the training process on artificial neural network [16].
The modified secant method is also used to determine the stress-strain relationship for Particle Reinforced Metal Matrix Composites (PMMCs), in a nonlinear manner using the Modified Secant Homogenization method. With the application of the methodology, the modified secant method predicts that the PMMC outcome criteria depend on mises and hydrostatic macroscopic pressure [17].
From the description of the research above, the Brent method has not tried to find the multiple root of an equation in the form of a polynomial. Both the conventional Brent method and the modified Brent method have not been able to find the multiple root value of an equation that has multiple roots. The selection of the initial value as proposed by Phinkam greatly influences the speed of convergence. In this study, the performance of the Brent method needs to be tested in finding the multiple root of an equation in the form of a polynomial. The Brent method is a hybrid of three methods, bisection, IQI and secant. The Brent method is considered better than other methods as described in previous studies.
The modified secant method is a more suitable method in calculating the search for multiple roots in polynomial equations [18]. In addition, the modified Newton-Raphson method is also more suitable in the search for multiple roots. The modified Newton-Raphson method and the modified secant method converge faster than the two conventional methods.
Materials and Methods
Research material
This study uses five types of multiple root polynomials.
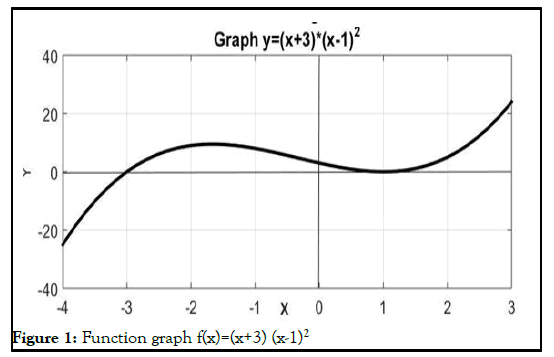
Function 1: f(x)=(x+3) (x-1)2
This equation has three roots and two of them have even multiple roots. The graph of the above function is illustrated in Figure 1;
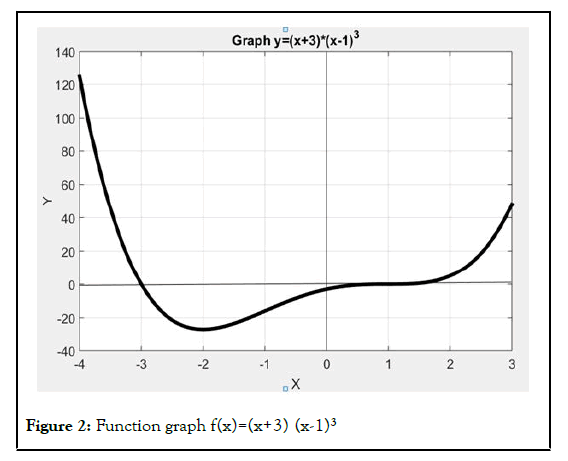
Function 2: f(x)=(x+3) (x-1)3
This function has four roots and three of them have multiple roots. The graph of the function is shown in Figure 2.
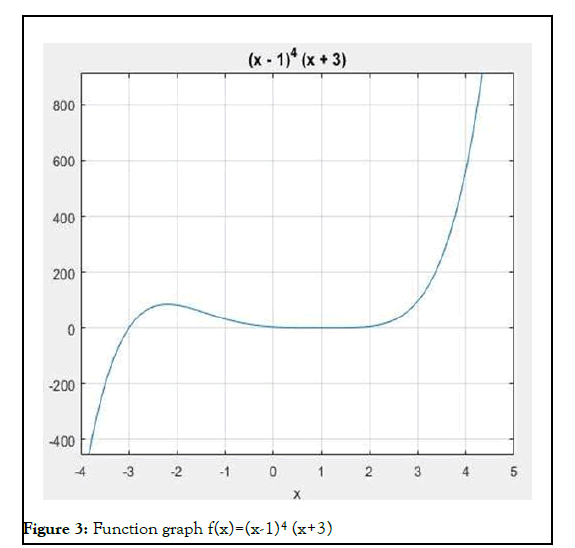
Function 3: f(x)=(x-1)4 (x+3)
This equation has five roots and four of them have multiple roots. The graph of this equation is shown in Figure 3.
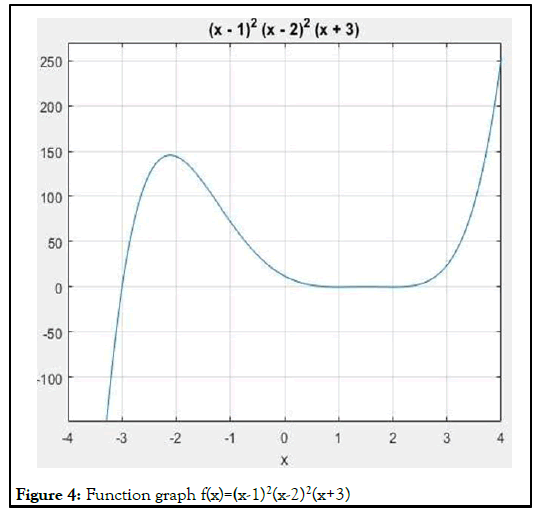
Function 4: f(x)=(x-1)2 (x-2)2 (x-3)2
The 4th equation has five roots and four of them have multiple roots with 2 pairs of different multiple roots each. The graph of the 4th equation is shown in Figure 4.
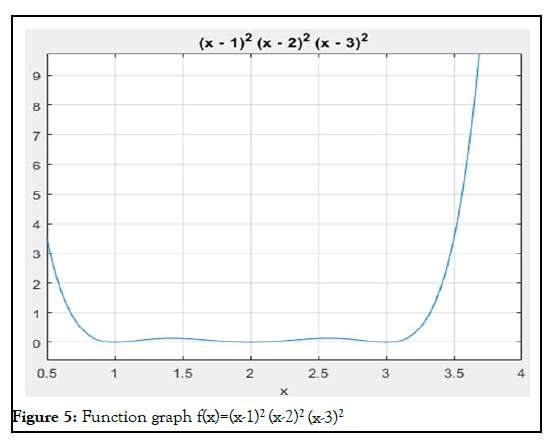
Function 5: f(x)=(x-1)2 (x-2)2 (x+3)
Equation (5) has six roots with three different pairs of multiple roots. The graph of the 5th function is shown in Figure 5.
Methods
The polynomials used are solved by 3 methods of finding roots. The three methods are the Brent method, the bisection method and the modified secant method.
Brent method algorithm
Input a, b: real; var c: real
Calculate f(a)
Calculate f(b)
If f(a) f(b)>=0 then error-exit end if
if |f(a)|<|f(b)| then swap (a, b) end if
c := a
set mflag
repeat until f(b or s) = 0 or |b−a| is small enough /* convergence */
if f(a) ≠ f(c) and f(b) ≠ f(c) then
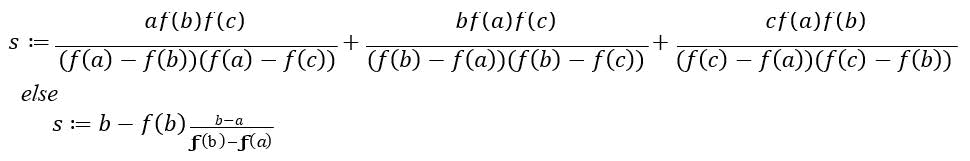
end if
if (condition 1) s is not between (3a + b)/4 and b
or (condition 2) (mflag is set and |s−b| ≥ |b−c|/2)
or (condition 3) (mflag is cleared and |s−b| ≥ |c−d|/2)
or (condition 4) (mflag is set and |b−c|<|δ|)
or (condition 5) (mflag is cleared and |c−d|<|δ|) then
s:=(a+b)/2 set mflag else
clear mflag end if calculate f(s)
d:=c
c:=b
if f(a)*f(s)<0 then b:=s else a:=s end if
if |f(a)|<|f(b)| then swap (a,b) end if end repeat
output b or s
Bisection method algorithm
• Specify the values of xl and xu to enclose the root, and make sure that the value of f(xl) × f(xu)<0, if it is greater than the root does not lie between the intervals xl to xu.
• Calculate the roots with the formula:.......l.ko xr=xl+xu/2
• Calculate the value of f(xl) × f(xr). If f(xl) × f(xr)<0, the root lies in the first sub interval, then xu=xr,go to step 4. If f(xl) × f(xr)>0, the root lies in the second sub interval, then xl=xr, go to step 4. If f(xl) × f(xr)=0, root=xr omputation is stopped.
• Calculate the new root with the equation: xr=xl+xu/2 • If the new root is accurate enough, stop computing, otherwise return to step 3.
Modified secant method
The equation of the modified secant method is obtained from the following process:
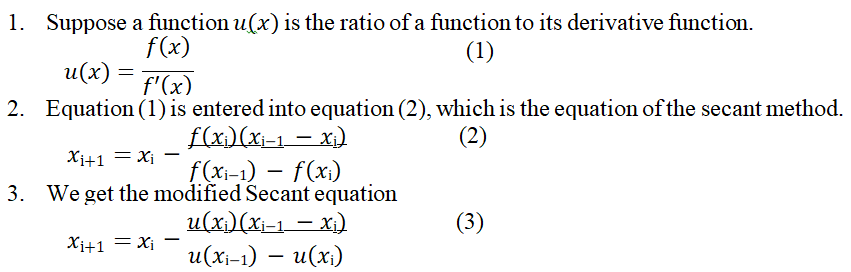
Equation (3) is a modified secant equation. The algorithm for the modified secant method is as follows:
• Determine initial value xi-1 and xi
• Determine the derivative of f (x)
• Calculate u(x) and u(x-1)
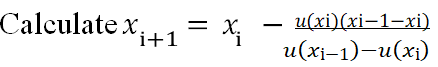
• The criterion stops on the secant method if the value of ���� (error approximation) is close to or equal to zero.
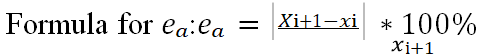
Results and Discussion
Root search results and number of iterations for each method
There are three methods used to solve the 5 polynomial equations above. The selection of initial values from the 3 methods is the same, both the lower and upper limits for the bisection method and the Brent method. The same value for the secant method for both xi-1 and xi values. In accordance with the algorithm of each method, the iteration stop criteria for the Brent method are if the value is f(s)=0.0000, the bisection method is f(xl) × f(xr)=0.00000 or ea=0.00000 value. The secant method, the iteration process is stopped if the approximation error value ea=0.00000.
Tables 1 to 5 show the calculation results of the three methods for each polynomial used.
Function 1: f(x)=(x+3) (x-1)2
| No | Initial Value | Searched root value | Iteration Number | |||||
|---|---|---|---|---|---|---|---|---|
| a=xl=i-1 | b=xu=xi | Brent | Bisection | Modified Secant | Brent | Bisection | Modified Secant | |
| 1 | 0.5 | 4 | Stop iteration | Stop iteration | 1 | - | - | 5 |
| 2 | -1 | 2.5 | Stop iteration | Stop iteration | 1 | - | - | 6 |
| 3 | -4 | 1.5 | 1.0039 | -3 | 1 | 10 | 16 | 6 |
| 4 | -4 | -2.5 | -3 | -3.00002 | -3 | 5 | 13 | 5 |
| 5 | -5 | 4 | -3 | -3.00008 | 1 | 9 | 11 | 7 |
Table 1: Comparison of the results of the modified Brent, bisection and secant methods for equation f(x)=(x+3) (x-1)2
Function 2: f(x)=(x+3) (x-1)3
| No | Initial Value | Searched root value | Iteration Number | |||||
|---|---|---|---|---|---|---|---|---|
| a=xl=xi-1 | b=xu=xi | Brent | Bisection | Modified Secant | Brent | Bisection | Modified Secant | |
| 1 | 0.5 | 4 | 1.047 | 1.1562 | 1 | 7 | 5 | 5 |
| 2 | -1 | 2.5 | 1.0404 | 1.0781 | 1 | 7 | 5 | 5 |
| 3 | -4 | 1.5 | Stop iteration | Stop iteration | 1 | - | 5 | - |
| 4 | -4 | -2.5 | -3 | -3 | -3 | 6 | 14 | 6 |
| 5 | -5 | 4 | Stop iteration | Stop iteration | 1 | - | - | 6 |
Table 2: Comparison of the results of the modified Brent, bisection and secant methods for equation f(x)=(x+3) (x-1)3
Function 3: f(x)=(x−1)4 (x+3)
| No | Initial Value | Searched root value and | Iteration Number | |||||
|---|---|---|---|---|---|---|---|---|
| a=xl=xi-1 | b=xu=xi | Brent | Bisection | Modified Secant | Brent | Bisection | Modified Secant | |
| 1 | 0.5 | 4 | Stop iteration | Stop iteration | 1 | - | - | 4 |
| 2 | -1 | 2.5 | Stop iteration | Stop iteration | 1 | - | - | 5 |
| 3 | -4 | 1.5 | -3 | -3 | 1 | 9 | 13 | 5 |
| 4 | -4 | -2.5 | -3 | -3 | -3 | 7 | 15 | 7 |
| 5 | -5 | 4 | -3 | -3 | 1 | 9 | 17 | 5 |
Table 3: Comparison of the results of the modified Brent, bisection and secant methods for equation f(x)=(x−1)4 (x+3)
Function 4: f(x)=(x−1)2(x−2)2(x+3)
| No | Initial Value | Searched root value | Iteration Number | |||||
|---|---|---|---|---|---|---|---|---|
| a=xl=xi-1 | b=xu=xi | Brent | Bisection | Modified Secant | Brent | Bisection | Modified Secant | |
| 1 | 0.5 | 4 | 1.047 | 1.1562 | 1 | 7 | 5 | 5 |
| 2 | -1 | 2.5 | 1.0404 | 1.0781 | 1 | 7 | 5 | 5 |
| 3 | -4 | 1.5 | Stop iteration | Stop iteration | 1 | - | 5 | - |
| 4 | -4 | -2.5 | -3 | -3 | -3 | 6 | 14 | 6 |
| 5 | -5 | 4 | Stop iteration | Stop iteration | 1 | - | - | 6 |
Table 4: Comparison of the results of the modified Brent, bisection and secant methods for equation f(x)=(x−1)2(x−2)2(x+3)
Function 5: f(x)=(x−1)2(x−2)2(x−3)2
| No | Initial Value | Searched root value and | Iteration Number | |||||
|---|---|---|---|---|---|---|---|---|
| a=xl=xi-1 | b=xu=xi | Brent | Bisection | Modified Secant | Brent | Bisection | Modified Secant | |
| 1 | 0.5 | 4 | Stop | Stop | 2 | - | - | 6 |
| iteration | iteration | |||||||
| 2 | 0.5 | 1.5 | Stop iteration | Stop iteration | 1 | - | - | 11 |
| 3 | -1 | 1.5 | Stop iteration | Stop iteration | 2 | - | - | 6 |
| - | - | 1 (there is a division by 0 for | ||||||
| 4 | 1.5 | 2.5 | Stop iteration | Stop iteration | 2 | the next iteration) | ||
| 5 | 1.5 | 3.5 | Stop | Stop | 3 | - | - | 5 |
| iteration | iteration | |||||||
| 6 | 2.5 | 4 | Stop | Stop | 1 | - | - | 13 |
| iteration | iteration | |||||||
| 7 | 2.5 | 3.5 | Stop iteration | Stop iteration | 3 | - | - | 8 |
Table 5: Comparison of the results of the modified Brent, bisection and secant methods for equation f(x)=(x−1)2(x−2)2(x−3)2
Discussion
From the results of the 2 Tables above, several things need to be explained as follows:
• The initial value selected to enclose the multiple roots, the Brent method and the bisection method could not find the search root. This happens because the bisection method algorithm cannot be continued if (a) × (b)>0, or Brent method if (a) × (b)>0, iteration process could not be contined. The process of finding the roots that are not found occurs in polynomial equations that have an even number of multiple roots such as polynomial equations f(x)=(x+3)(x−1)2, function f(x)=(x−1)4(x +3), function f(x)= (x−1)2(x−2)2(x+3) and function f(x)= (x−1)2(x−2)2(x− 3)2. In Table 1, Table 3, Table 4 and Table 5 it can be seen that by selecting the initial value that encloses the multiple root of the Brent method and the bisection method, it cannot find the root you are looking for.
• It is different if the initial value is selected in the polynomial equation mentioned in point a) above, the selected initial value encloses one of the roots that are not multiple roots or encloses all roots of the Brent method and the bisection method will produce the root you are looking for. The value of the root to be sought is one root not multiple roots for the polynomial equation f(x)=(x+3)(x−1)2, function f(x)=(x−1)4(x+3), function f(x)=(x−1)2(x−2)2(x+3).
• Despite selecting the initial value that encloses all the roots in Table 5, the Brent and bisection methods could not find the root we were looking for, (data in Table 5), for the polynomial with equation f(x)=(x-1)2(x−2)2(x−3)2.
• In contrast to polynomials that have an odd number of multiple roots,f(x)=(x+3) (x−1)3, Brent and Bisection methods can find multiple roots. The selection of initial values that confine the multiple roots, both the bisection method and the Brent method, the search for the roots obtained the results of the multiple roots. Meanwhile, if the determination of the initial value encloses all the roots, the Brent method and the bisection method cannot determine any of the roots being sought. According to the algorithm, the two methods cannot be continued because the multiplication value of the value function of the selected initial value is greater than 0.
• In contrast to the modified secant method, determining the initial value chosen for an even or odd numbered twin-rooted polynomial equation, the results of the root search will be obtained. The initial value that encloses one of the multiple roots or all multiple roots always produces the searched root. Seen in table 1 to table 5.
• The modified secant method, even though the selected xi-1 and xi values enclose one root instead of a multiple root, the results obtained from the modified secant method remain multiple roots. Likewise, if the initial value selection does not enclose multiple roots or one of the roots, the modified secant method still produces multiple roots.
• There are similarities between these three methods in generating the sought root. All three methods produce the same root value if the specified initial value encloses all roots, both multiple roots and one of the other roots. The result obtained is a root that is not a multiple root. It can be seen in Table 1, Table 2, Table 3, Table 4 and Table 5, which are polynomial equations that have other than multiple roots but also one other root.
• In terms of the speed of convergence, in Table 1, for the function f(x)=(x+3) (x−1)2, the Brent and secant methods converge faster th an the bisection method. The root searched from both methods.
Conclusion
Comparison of the results of the Brent, bisection and secant methods can be seen in the trials of polynomials which have multiple roots. Several conclusions can be drawn from this research as well as suggestions that need to be developed for the search for polynomial roots that have multiple roots
• The Brent method and the bisection method cannot find the roots of a polynomial whose roots are all multiple roots.
• The Brent method and the bisection method can find the multiple root of a polynomial on the condition that the polynomial, apart from having multiple roots, also has one other root. In addition, the number of multiple roots that the polynomial has is odd. The selection of the initial value of the bisection method and the Brent method must enclose the multiple root of the polynomial. If you confine all the roots it produces one other root.
• Root search using the modified secant method is very effective and the speed of convergence is higher than the bisection method and the Brent method. The secant method can produce a multiple root search with a random selection of initial values.
• The problem with the secant method is that it is necessary to find the derivative of the polynomial function. It will be difficult and will not result in finding the root, if there is a division by zero.
• For further research, the use of the Brent method, especially the search for multiple roots of a polynomial, it needs to be modified again. As discussed earlier, the Brent method cannot produce a root search because the algorithm conditions are f(a) × (b)>0. It is necessary to develop a new formulation, so that these conditions can be eliminated. Thus the multiple roots of a polynomial can be found using the Brent method.
Data Availability
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
Conflict of Interest
The authors declare that they have no conflict of interest.
References
- Kim T, Noh W, Oh S, et al. An improved hybrid algorithm to bisection method and Newton-Raphson method. Appl Math Sci. 2017; 11(56):2789–97.
- Pinkham S, Sansiribhan S. A new hybrid algorithm of bisection and modified Newton’s method for the nth root-finding of a Real Number. In Journal of Physics: Conference Series 2020; 1593(1).
- Ehiwario JC, Aghamie SO. Comparative study of bisection, Newton-Raphson and secant methods of root-finding problems. IOSR J Engineer. 2014;4(4):01-7.
- Rasheed M, Shihab S, Rashid T, Ounis TD. Determination of PV model parameters using bisection and secant methods. J Math Comput Sci. 2021;13(1):43.
- Gemechu T. Root finding for nonlinear equations. Math. Theory Model. 2018;8(7):1-0.
- Sharma JR, Kumar S. An excellent numerical technique for multiple roots. Math Comput Simul. 2021;182:316-24.
- Ezenugu AI, Onwuzuruike VK. Analysis of secant algorithm for optimal path length of point-to-point microwave link. Int J Sci Res Eng. Trends. 2019;5(1):146-50.
- Etin-Osa BF, Noah CT. On a one fixed point improved secant method for solving roots of polynomials. J Math Sci. 2020;3(1):83-93.
- Muhammadsharif FF, Hashim S, Hameed SS, et al. Brent’s algorithm based new computational approach for accurate determination of single-diode model parameters to simulate solar cells and modules. Solar Energy. 2019;193:782-98.
- Han Z, Jin H, Fu Y, et al. Cutting deflection control of the blade based on real-time feedrate scheduling in open modular architecture CNC system. Int J Adv Manuf Technol. 2017;90(9):2567-79.
- Vakkalagadda SSP. A better root finding method using false position and inverse quadratic interpolation methods. Int Researh J Eng Technol. 2020;7(4):4178–80.
- Rahman NA, Abdullah L, Ab Ghani AT, et al. Modified Brent’s method for solving interval type-2 fuzzy polynomials. Far East J Mathem Sci. 2017;102(6):1099-113.
- Yuanzheng L, Shufa L, Jiang H, et al. A New Auto-balancing algorithm based on brent's method for impedance measurements. In Proceedings of the 2019 2nd International Conference on Algorithms, Computing and Artificial Intelligence 2019;73-7.
- van LBS, Ten TBJH, IJzerman WL. Full linear multistep methods as root-finders. Appl Math Comput. 2018;320:190-201.
- IE Livieris, Pintelas P, “A new class of spectral conjugate gradient methods based on a modified secant equation for unconstrained optimization,” J Comput Appl Math, 2013;239(1):396–405.
- Livieris IE, Pintelas P, “A new conjugate gradient algorithm for training neural networks based on a modified secant equation,” Appl Math Comput, 2013;221:491–502.
- Vinuela JZ, Perez-Castellanos JL. A particular implementation of the Modified Secant Homogenization Method for particle reinforced metal matrix composites. Composite Structures. 2014;109:260-7.
- Chapra SC, Canale RP, Numerical methods for engineers, second edition, SIXTH. The McGraw-Hill Companies, Inc, 2006.