The generating function technique and algebraic ordinary differential equations

Robert Lloyd Jackson

doi:10.37532/2752-8081.23.7(2).65-69.

Robert Lloyd Jackson^*

Independent Researcher, Stilwell, Kansas 66085, USA, Email: rljacksonmd@gmail.com

^*Correspondence: Robert Lloyd Jackson, Independent Researcher, Stilwell, Kansas 66085, USA, Email: rljacksonmd@gmail.com

Received: 13-Jan-2023, Manuscript No. puljpam-23-6177; Editor assigned: 14-Jan-2023, Pre QC No. puljpam-23-6177 (PQ); Accepted Date: Mar 10, 2023; Reviewed: 16-Jan-2023 QC No. puljpam-23-6177 (Q); Revised: 17-Jan-2023, Manuscript No. puljpam-23-6177 (R); Published: 31-Mar-2023, DOI: 10.37532/2752-8081.23.7(2).65-69.

Citation: Jackson RL. The generating function technique and algebraic ordinary differential equations. J Pure Appl Math. 2023; 7(2):65-69

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

In the past, theorems have shown that individuals can implement a (formal) power series method to derive solutions to Algebraic Ordinary Differential Equations, or AODEs. First, this paper will give a quick synopsis of these “bottom-up” approaches while further elaborating on a recent theorem that established the (modified) Generating Function Technique, or mGFT, as a powerful method for solving differentials equations. Instead of building a (formal) power series, the latter method uses a predefined set of (truncated) Laurent series comprised of polynomial linear, exponential, hypergeometric, or hybrid rings to produce an analytic solution. Next, this study will utilize the mGFT to create analytic solutions to a several example AODEs.Ultimately, one will find mGFT may serve as a powerful "top-down" method for solving linear and nonlinear AODEs.

Keywords

Algebraic Ordinary; Differential Equation; Generating Function Technique; Power Series

Introduction

The AODEs use differential algebra to define differential equations with only one independent variable [1]. Numbers theory and computer-based algebra are extensively utilized and supported by this field. Finally, AODEs have many formulations, such as differential Galois theory and modules (i.e., M, D, etc.).

Most methods for solving AODEs involve a “bottom-up” approach regarding a formal power series. In other words, an individual tries to establish an analytic solution by finding a pattern within the leading coefficient of a solitary power series [2]. If the value turns out to be a combinatorial number, then the power series becomes formal [3]. This process often involves enacting many iterations, making the "bottom-up" means of acquiring an analytic solution very time-consuming [2-3].

This article will consider a new “top-down” approach for finding solutions to AODEs. It is well-known that (formal) power series can form a new analytic function [4]. For instance, GFT, which incorporates a set of Laurent series of product ring-based formal power series or generating functions, can be used to discover analytic solutions to both linear and nonlinear partial differential equations [5]. This method might be the pinnacle of power series methods to develop new functions; hence, mGFT is viewed as a “top-down” means for solving differential equations, such as AODEs, since it uses preformed generating functions to find analytic solutions.

There are several sections in this paper. Section two will have a more thorough discourse on methods and theorems which implement a "bottom-up" basis for deriving analytic solutions to AODEs. On the other hand, the theorem explaining why mGFT, an effective “top-down” instrument in solving nonlinear partial differential equations, will be further elucidated and expanded upon (in regard to Ring Theory) to show it as a method for finding solutions AODEs in section three. Section four will show the application of mGFT on a few examples of AODEs. Finally, the conclusion, or section five, will gleam a terse description and beneficial facets of mGFT.

(Formal) Power series and their solutions to AODEs

Consider the following power series, also known as a Taylor series:

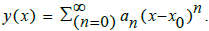
equation

If x_0, or the center of the series, was equal to null or zero, then the above expression is considered a Maclaurin series. Some coefficients an of a power series incorporated a division by factorial n. It was the main purgative for an individual to define the value of this coefficient for each serial term [6]. Also, the Cauchy-Hadamard theorem stated that power series converged at specific values: when a series was deemed convergent, it formed an analytic function [7-9].

There were many algorithms and methods for establishing power series solutions to various differential equations via iterative or “bottom-up” means. For instance, N. Thieu Vo and associates devised an algorithm that helped an individual iteratively access each coefficient of a prospective power series solution to an AODE [10]. Building an analytic solution via single power series is generally time-consuming, but others in the field are finding ways to accelerate the process [11].

The generating function technique revisited

The central theorem that established the GFT as a method for solving (nonlinear) PDEs claimed that a (truncated) Laurent series of formal power series derived analytic solutions to many (nonlinear) differential equations [5]. The theorem suggested that formal power series within the set of (truncated) Laurent series are polynomial rings. Upon applying the polynomial rings within a differential equation, an individual would form a free ideal ring whose generators were necessary to form algebraic equations. Setting these algebraic equations to zero, then solving for as many coefficients and constants as possible would allow the individual to establish analytic solutions to many differential equations.

Definition 1

The predefined set of (truncated) Laurent series of generating functions served as the general solution to an AODE of interest and was a symmetric (Lie) algebra.

Definition 2

The auxiliary function f_l, in the primary expression defining the general solution y, was a polynomial ring based upon the dependent variable, or intermediate, x. The dependent variable x was linearized, exponentiated, or hypergeometric transformed.

Definition 3

The multiplication of auxiliary functions f_l established a polynomial product ring.

The general solution y of mGFT was defined as follows:

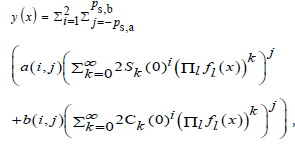
equation

where is the l-th auxiliary function, and were the square root of the Fibonacci and Chebyshev U combinatorial numbers about zero, respectively. Note:

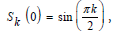
equation

and

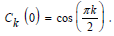
equation

The other coefficients accompanying each formal power series or generating function were a(i, j) and b(i, j). The set of Laurent series, which was truncated by the specific powers p_s,a and p_s,b, of formal power series or generating functions were used in the general solution were "complete" polynomial rings.

Note: the general solution y with a Frobenius adjustment was:

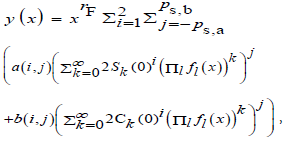
equation

For this paper's purpose, we defined the auxiliary function as a linearized, exponentiated, or hypergeometric transformed polynomial ring . The polynomial ring was defined as:

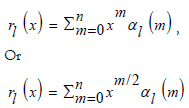
equation

where α_l was a coefficient/constant and 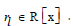equation (Note: theformer auxiliary function f₁ was used in the rest of this section and for deriving solutions to the example AODEs given in the next section of this study since it possessed a significantly lower computational cost than its counterpart.) The auxiliary function f₁ of the predefined formal power series or generating function was either linearized (l=1), exponentiated (l=2), transformed (l=3),or a combination of at least two of the three last states [12-13]. Thus:

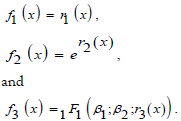
equation

If the auxiliary function f₁ was only in the predefined formal power series, then the resultant general solutions would be comprised of polynomial linear rings. If the auxiliary function f₂ was only in the predefined formal power series, then the resultant general solution would be made of polynomial exponential rings. It was important to note that the paper introducing GFT only considered (a variation of) the auxiliary function f₂ with a truncated polynomial ring r₂(x) [5].If the auxiliary function f₃ was only in the predefined formal power series, then the resultant general solution would consist of polynomial hypergeometric rings. Finally, if at least two of the three auxiliary functions f₁, f₂, and f₃ were in the predefined formal power series, then the resultant general solution would be comprised of polynomial hybrid rings. Since one considered the composition of formal power series as a set of polynomial rings, could claim each completed polynomial ring was a symmetric algebra [14].

For clarification purposes, regular GFT is when an individual considers at least one of the three auxiliary functions with the "primary" ansatz transform variable in the general solution while modified GFT is when an individual incorporates the Frobenius and/or other correction, such as an exponentiated additional ansatz transform variables, into the general solution via simple multiplication. One should also consider GFT has undergone some form of modification when additional ansatz transform variables exist within at least one of the three auxiliary functions.

Lemma and definition 4

Plugging the set of (truncated) Laurent series of polynomial rings described above into an AODE of interest and possibly considering some hypergeometric function contiguous relations established Hopf algebras.

Lemma 5

Multiplying the Hopf algebras with the multiplicative inverse of the greatest common (zero) divisor, followed by parsing the resultant principal integral/ideal domain or free ideal ring by the generators of the transformed AODE of interest that were associated with auxiliary functions f₁, f₂, and f₃, produced algebraic equations.

Substituting the general solution into AODEs established Hopf algebras known to be skewed polynomial rings called noncommutative principal ideal rings, or R_PI [15]. Sometimes the Hopf algebras did not become apparent until an individual considered hypergeometric function contiguous relations. When an individual multiplied the transformed AODEs with its common denominator/multiplicative inverse of the greatest common (zero) divisor, or (R_GCD)⁻¹, (s)he obtained a particular product ring, calleda principal integral/ideal domain, or R_PID [16]. In other words, the numerator of a principal ideal ring was a principal ideal domain.

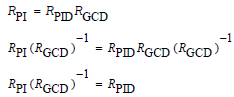
equation

A principal integral/ideal domain was also known as a free ideal ring or fir [17]. Also, it was necessary to note that if one considered the auxiliary function f₃ was present in the general solution, they had to include the contiguous relations of the hypergeometric function after plugging in the general solution into the AODE. For example, the derivatives of 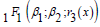equation in the transformed AODE wereconverted to expressions involving 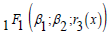and 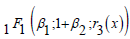before proceeding.

A set of generators parsed the principal integral/ideal domain or free ideal ring into many symmetric algebraic equations. The gathering of linearized, exponentiated, and/or hypergeometric transformed polynomial ring of variable/intermediate x, like

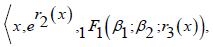
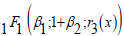equation

equation may serve as the generator set for the R_PID produced from some AODEs. (For instance, the parsing of a R_PID may have only used part of the entire possible generator set, like 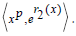It was important to state the generator 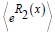was able to be expanded to its individual exponential terms and itself.

For instance,

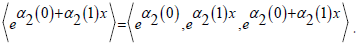
equation

The generator set was used to derive more algebraic equations by parsing the product ring R_PID [5]. These algebraic objects were also likely symmetric.

Corollary

By setting the algebraic equations derived from the product ring discussed above to null or zero, an individual should be able to define at least one set of coefficients/constants properly. After plugging these coefficients/constants into the set of (truncated) Laurent series of polynomial rings described in definition 3.1, the last item may become an analytic solution to the AODE of interest.

One exploited the algebraic equations for the values of the coefficients/constants and possiblyFr whenever possible after setting all the algebraic equators equal to null or zero. Using computer mathematics software, like Mathematica®, individuals derived sets of known coefficients/constants that yielded analytic solutions to AODEs.

It was important to note that when the AODE contained variable coefficients and inhomogeneous components that were either exponential or trigonometric functions, an individual had to limit the auxiliary function f_l as an exponentiated expression of the independent variablex, or let l=2.

Mathematica was used to derive solutions to the following AODEs. Thus, one was able to follow most of the work in this paper by examining the Mathematica spreadsheet

Examples

This study section will consider and solve three examples AODEs found within the Kamke set [18]. The first equation, ODE No. 29, in the paper is as follows:

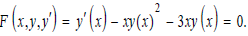
equation

By setting the domain of ps of the general solution between (0, 2), then plugging it into the above equation, one obtains a significant expression involving the variable x. Next, times the common denominator/multiplicative inverse of the expression's greatest common (zero) divisor with the original equation/principal ideal ring to derive a product ring or free ideal ring. The following generator set,

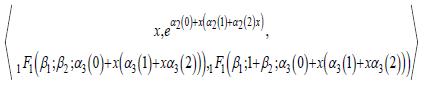
equation

creates one hundred fourteen algebraic equations, or:

equation

After setting these algebraic equations to null or zero, one derives nineteen sets of coefficients/constants, thus possible analytic solutions. The expression below is an example of an analytic solution derived for AODE given above:

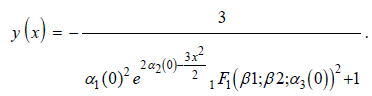
equation

Another AODE from the Kamke set is ODE No. 1115:

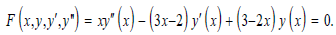
equation

By setting the domain of ps of the predefined set of (truncated) Laurent series consisting of formal power series also between (-1, 0), then plugging it into the above equation, one obtains a significant expression involving the variable x. Again, times the common denominator/multiplicative inverse of the expression's greatest common (zero) divisor and the equation itself to derive a product ring or free ideal ring. The following generator set,

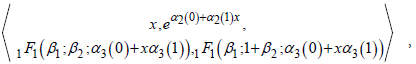
equation

yields 57 algebraic equations. After solving for the coefficients/constants, one derives one hundred 86 sets of possible solutions. The following is an example of an analytic solution derived by mGFT for the above AODE:

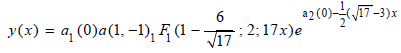
equation

Next, the ODE No. 1700 from the Kamke set is considered:

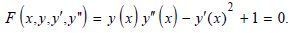
equation

By setting the ps domain of the general solution again between (-1,0), then plugging it into the above equation, one produces a significant expression involving the variable x. Again, multiplies the common denominator/multiplicative inverse of the greatest common (zero) divisor of the expression and the equation itself to derive a product ring or free ideal ring. The following generator set,

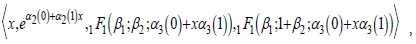
equation

establishes fifty-two algebraic equations. After solving for the coefficients/constants, one generates forty-six different results. An example of an analytic solution derived by [m]GFT for the above AODE is as follows:

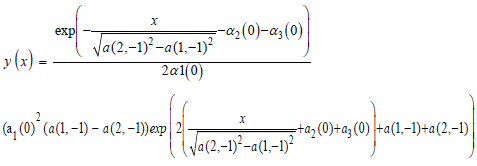
equation

The final AODE from the Kamke set is ODE No. 1483:

equation

By setting ps of the general solution with the Frobenius correction to negative unity or -1, then plugging it into the above equation, one produces a significant expression involving the variable
x. Again, (s)he multiplies the common denominator/multiplicative inverse ofthe greatest common (zero) divisor of the expression and the equationitself to derive a product ring or free ideal ring. The followinggenerator set,

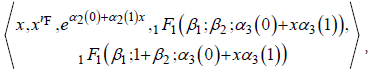
equation

creates 29 algebraic equations. After solving for the coefficients/constants, an individual generates 61 different results. An example of an analytic solution derived by [m]GFT for the above AODE is as follows:

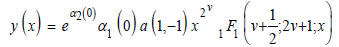
equation

Conclusion

Unlike many "bottom-up" methods that build analytic solutions from solitary (formal) power series, mGFT uses a set of (truncated) Laurent series of predefined polynomial linear, exponential, hypergeometric, or hybrid rings to establish analytic solutions to differential equations. Finally, mGFT is not only a powerful tool for solving (nonlinear) partial differential equations but also possesses excellent potential to find analytic solutions to many linear and nonlinear differential equations, unlike other methods.