The K-equivalent, function equivalence in sense of Kamtchueng

Received: 12-Nov-2023, Manuscript No. puljpam-24-6960; Editor assigned: 15-Nov-2023, Pre QC No. puljpam-24-6960 (PQ); Accepted Date: Jan 29, 2024; Reviewed: 18-Nov-2023 QC No. puljpam-24-6960 (Q); Revised: 21-Nov-2023, Manuscript No. puljpam-24-6960 (R); Published: 31-Jan-2024, DOI: 10.37532/2752-8081.24.8(1).01-02

Citation: Kamtchueng C. The K-equivalent, function equivalence in sense of Kamtchueng. J Pure Appl Math. 2024; 8(1):01-02.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

An open question relative to the definition domain of a polynomial function given by the following expression push us to define new relation between functions. By simple element
decomposition, one could find but even if intuitively the functions are equivalent, the first one is not defined for in order to avoid the denominator to be null. In this short paper, we want to find the intuition back by defining a new relationship between two functions.

Key Words

Polynomial; Equivalence

Introduction

This article is based on a reflexion from an exercice, I asked to my students if the two following function were equivalent.

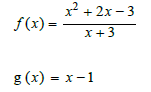
We consider two new types of functions: g_a(x) equal to x-1 if x≠−3 and a otherwise 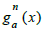equal to x-1 if x≠−3 | and 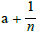otherwise

The point of this article is to introduce the Kamtchueng Equivalence of the two functions.

K-Equivalence

Theorem: f is K-equivalence to g under D_f∪{x₀} if and only if for all x₀ where f is not defined there is a compact centered in x₀ such as for all x ≠x₀ within the compact, limit of f(x) when x tends x˙ equal to
g(x˙).

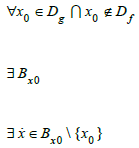
By definition of the K-Equivalence, one domain should be included strictly to the other, which is not the case for D_g.

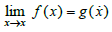
With B_x0 a compact centered in x₀ no empty and different of the singleton.

This definition can be extended to function domain with a countable number of not included points.

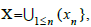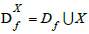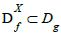Theorem: Set is K-equivalent to g under with if and only if

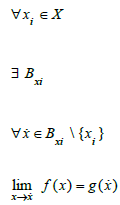
The K-Equivalence is not commutative.

f K-Equivalent to g does not imply that g K-Equivalent to f under D

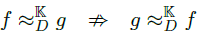
Demonstration: by considering the two functions f and g defined in Introduction, we have f Kequivalent to g but g is not K-Equivalent to f. Indeed the definition domain of g not included in the domain of f.

The K-Equivalence is transitive.

f K-Equivalent to g under and g K-Equivalent to h under imply that f K-Equivalent to h under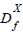

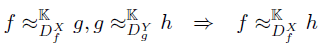
Demonstration:

Set 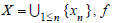is K-equivalent to g under D = D_f ∪X with D ⊂ D_g if and only if

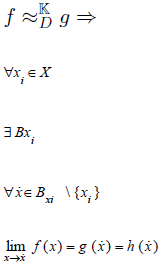
Indeed 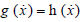the because of the 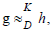therefore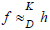

Conclusion

Lets focus on the function defined in Introduction f and g but also:

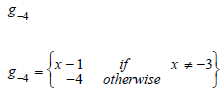
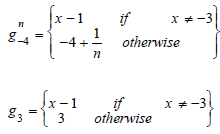
In one hand, g = g_-4 but f ≠g because of the apparent definition domain of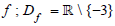

In another hand 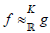therefore 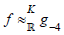It is interesting to note that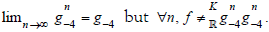

In addition, 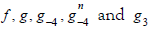are equals in D_f

Firstly, what happen to the K-Equivalence when the non-defined set is not countable? Secondly is this definition really necessary? Are these functions really differents? what about all the

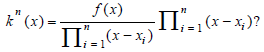
Lets imagine two students look at a car, one say that the car is blue but the other one say that the car is green. The first one state that he believed it was green before but the builder of car state that the car is blue. If the builder say it but it is not so obvious, the second decide to create a color green blued which is very similar to green. At the end, maybe the car builder has done a mistake in fact one of the painting machine was leaking micro test of blue. Therefore even if it is neglieable the autochecker was telling the color blue instead of green... If it is the case, we create a new color especially for it! Would it have been better to just consider it as a mistake?