The Michelson-Morley experimentΖs proper formulas
Received: 06-Jan-2023, Manuscript No. PULJPAM-22-6024; Editor assigned: 09-Jan-2023, Pre QC No. PULJPAM-22-6024 (PQ); Reviewed: 23-Jan-2023 QC No. PULJPAM-22-6024; Revised: 22-Mar-2023, Manuscript No. PULJPAM-22-6024 (R); Published: 30-Mar-2023, DOI: 10.37532/PULJPAM.2023.7(3).140-142
Citation: Akram L. The Michelson-Morley experiment's proper formulas. J Pure Appl Math 2023;7(3):140-142.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
When the light photons bounce off a moving mirror, they react with its atoms to be reflected, consequently, the photons change their velocity vector after each impact depending on the velocity vector of the mirror and thus of the atom. The Michelson-Morley experiment was the event that changed the modern science about "the light" by leading to Lorentz and Einstein's theories about time. I made the formulas of the michelson-morley experiment by considering the effects of the reflection on the light and the rate (percentage) of fringe shift calculated by the formulas which I demonstrated is perfectly null. As a result, not all physics must be wrong, but only a principle that Einstein and Lorentz stated by fixing the light speed for all observers, which makes us study light in a very difficult way. The formulas demonstrated in this work allow us to study the light as a normal wave and to understand easily all the other light effects without being obliged to use any relativity of the time.
Keywords
Michelson; Morley; Light photon; Interferometry; Mirror; Reflection; Absorption; Emission; Null result; Reference frame; Speed of light; Relativity
Introduction
The speed of light has been calculated by maxwell after fixing the electric and magnetic characteristics of the source and of the empty space [1-3]. However, the special relativity considers that the speed of light can only be constant for all observers thanks to the Michelson-Morley experiment [4-7]. It is a theory that has been tested by Kennedy-Thorndike experiment, Ives- Stilwell experiment and many others [8-11]. This theory is also used when dealing with moving light clocks [12]. And when performing experiments by using lattice clocks [13].
Many works still try to present this theory as a correct theory by daring to curve theoretically the space time while other rational thinkers stay aware that our space is obviously the Euclidean space and they prove it by their realistic physics works [14,15].
Literature Review
Some researchers refuse both the special relativity and the general relativity and try to disprove their mathematical tools or to prove that the luminiferous aether exists or that the relativistic demonstrations can be replaced by easy Newtonian demonstrations.
The steps explained in this work when dealing with the light reflection give correct answers and should help to avoid the complicated relativity of time especially in Michelson’s interferometer. In this work, we will prove formulas that predict the null result of Michelson-Morley experiment.
Since we are verifying the experiment results of michelson-morley, we are free to change the light velocity vector when it is reflected.
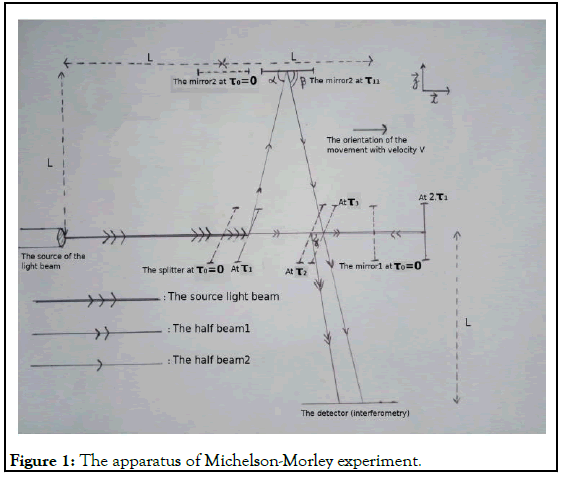
We consider that T1 and T2 are the two times needed by the two half beams to reach the captor starting from the source, and that the splitter doesn’t influence the light when it passes without any deviation through it, otherwise we will have to use compensating plates to correct that.
When a light photon bounces off a moving mirror, it reacts with one of the mirror’s atoms to be reflected through the absorption then the emission. Consequently, the photon gets also an additional velocity vector. It is the velocity vector of the atom during the emission and thus of the mirror. This phenomenon is similar to a ping pong ball bouncing without slipping inside a box that is moving side wards. In this case the ping pong ball gets the box velocity as a side wards component of its velocity vector after it bounces and thus the ball seems to accompany the box in its movement.
Discussion
In this work, v is the velocity vector of the mirrors and C1 is the speed of the light directly after the source. We can consider that: C1=C if the source of the light is fixed during the experiment, where C is the famous speed
constant of the light. And we can consider that: C1=C+V if the source of the light moves during the experiment with the velocity V. However, the detector (interferometry) is considered always fixed during the experiment.
The proposed approach
The Figure 1 describes the paths taken by the light beams in Michelson- Morley experiment. In this figure we considered arbitrarily that α=ϐ but γ different. Also τ2 and τ3 are arbitrarily considered different until this work makes the investigation.
The half beam 1 is the one reflected from the mirror 1 and the half beam 2 is the one reflected from the mirror 2.
For half beam 1
We can prove that:
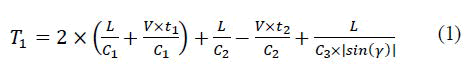
(Each term is explained down)
By considering that:
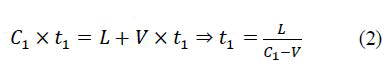
where t1 = τ1
C2 is the speed of the light returning after being reflected from the mirror 1.
During the reflection operation of the light, the speed of the light photon absorption by the reacting atom of the mirror is C1-V. Consequently, the photon will be emitted with the same speed (same energy at the absorption) relatively to the reacting atom along the same axis ī . However, since the atom is moving during the emission with a speed V × ī then: C2 = C1 – 2 × V (3)
By considering also that:
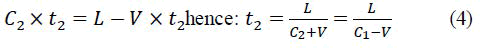
where: t2=τ2−2 × τ1
And that C3 is the speed of light after being reflected from the splitter and before reaching the detector. The speed of the light photon absorption by the reacting atom of the splitter is: C2+V=C1-V consequently, the photon will be emitted perpendicularly along the axis j with the same speed (same energy at the absorption) relatively to the reacting atom. However, since the reacting atom moves during the emission along the axis ī with the speed V, then V × ī will be in this case a component of the emitted photon velocity vector. In the end, the velocity vector will become:
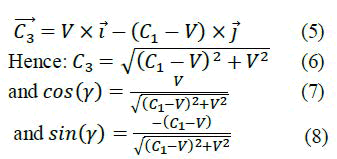
And by considering that t3 is the time needed by the light to reach the detector after being reflected from the splitter, we have:
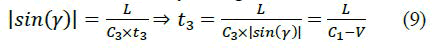
We deduce that:
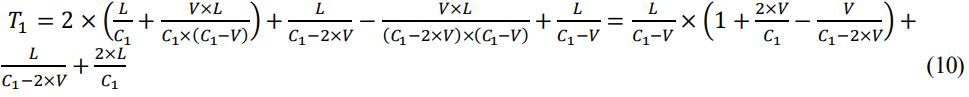
For half beam 2
By following the same steps, we can prove that:
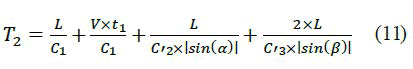
(Each term is explained down)
By considering that: C'2 is the speed of the light after being reflected from the splitter and before reaching the mirror 2.
Consequently:
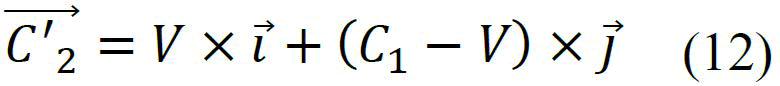
(Similar to the case of C3 with half beam 1)
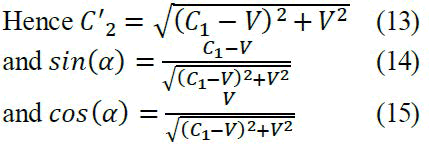
And also by considering that: C'3 is the speed of the light after being reflected from the mirror 2 and before reaching the captor. The speed of the light photon at the absorption is:
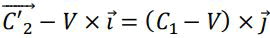
Consequently, the photon will be emitted with the same speed (same energy at the absorption) relatively to the reacting atom. However, since the reacting atom moves during the emission along the axis ī with the speeds V.
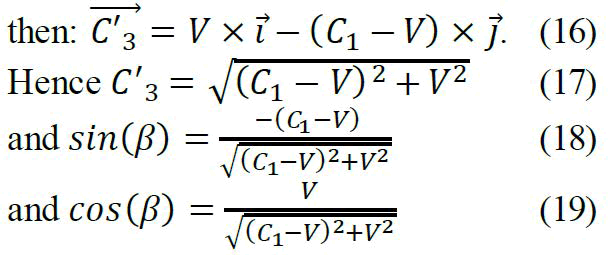
We deduce that:
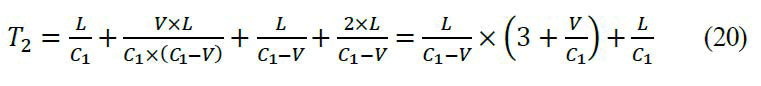
Finally:
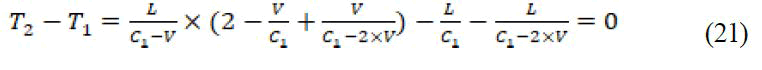
Remarks:

Hence they become parallel before reaching the detector at exactly the same time.
Conclusion
The result is made by considering that the speed of light changes by the changing reference frames since this work tests the results of Michelson- Morley experiment and doesn’t consider that Einstein’s conclusion about the luminiferous aether is correct.
The rate (percentage) of fringe shift by the formulas demonstrated above is null and thus it confirms theoretically that the result of Michelson-Morley experiment is perfectly null. However, we can’t conclude that the luminiferous aether doesn’t exist like Einstein said or that the speed of the light doesn’t change by a changing reference frame.
References
- Longair MS. Maxwell and the science of colour. Philos Trans A Math Phys Eng Sci. 2008;366(1871):1685-96.
[Crossref] [Google Scholar] [PubMed]
- Louiz A. The correct formulas of Michelson-Morley experiment. Maghreb J Pure Appl Sci. 2020;6(2):60-4.
- Michelson AA, Pease FG, Pearson F. Repetition of the Michelson-Morley experiment. J Opt Soc Am. 1929;18(3):181.
- Szostek K, Szostek R. The explanation of the Michelson-Morley experiment results by means universal frame of reference. J Mod Phys. 2017;8(11):1868.
- Croca JR, Moreira R, Gatta M, et al. Experiments on the speed of light. J Appl Math Phys. 2019;7(5):1240.
- Gurzadyan VG, Margaryan AT. The light speed versus the observer: The Kennedy–Thorndike test from GRAAL-ESRF. Eur Phys J C. 2018;78:1-6.
- Rindler W, Salisbury D. Relativity: Special, general, and cosmological. Am J Phys. 2003;71(10):1085-6.
- Sfarti A. Optical clock behavior in a gravitational field. Int J Photonics Opt Technol. 2018;4(3):20-3.
- Takamoto M, Ushijima I, Ohmae N, ET AL. Test of general relativity by a pair of transportable optical lattice clocks. Nat Photonics. 2020;14(7):411-5.
- Bongs K, Singh Y. Earth based clocks test general relativity. Nat Photonics. 2020;14(7):408-9.
- Torrome RG. Maximal acceleration geometries and space time curvature bounds. Int J Geom Methods Mod Phys. 2020;17(04):2050060.
- Shirokov D. On constant solutions of SU (2) Yang-Mills equations with arbitrary current in Euclidean space. J Nonlinear Math Phys. 2020;27(2):199-218.
- Zhang C, Jiang J, Zhao Y. Euclidean space with orbital angular momentum. IEEE International Conference on Communications Workshops (ICC Workshops). IEEE. 20-24 May 2019, Shanghai, China. 2019;1-6.
- Sato M. De broglie waves, the schrodinger equation, and relativity. I. Exclusion of the rest mass energy in the dispersion relation. Physics Essays. 2020;33(1):96-9.
- Louiz A. A thesis about Newtonian mechanics rotations and about differential operators. Maghreb. J Pure Appl Sci. 2020;6(1):26-50.