THE MODIFIED VARIATIONAL ITERATION METHOD AND FOURIER SERIES FOR SOLVING INHOMOGENEOUS ORDINARY DIFFERENTIAL EQUATIONS

Received: 25-Oct-2021 Accepted Date: Nov 09, 2021; Published: 16-Nov-2021

Citation: Geremew S, Gutema T. The Modified Variational Iteration Method and Fourier series for Solving Inhomogeneous Ordinary Differential Equations. J Pur Appl Math. 2021; 5(6):86:88.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

In this paper,a formula of modified variational iteration method and Fourier series for solving linear and nonlinear non-homogeneous differential equations is derived. Particularly the method is derived and applied to nonhomogeneous differential equation. If the non-homogeneous part of the equation is non-continuous periodic function with a period 2π.

Keywords

Modified variational iteration method; Fourier series; Ordinary differential equations

Introduction

Most of the nonlinear ODEs have no explicit solutions and too complicated to analyze the principal fea- tures of this solution.

Hence the study of nonlinear mathematical problems is the most time-consuming and difficult task for researchers dealing with nonlinear models in the natural sciences, engineering, and scientific computing. A variety of analytical asymptotic and approximation techniques have been developed in recent years to determine approximate solutions. Among of these techniques the varia- tional iteration method is one [1]. The variational iteration method gives rapid convergent successive approximations without any restrictive assumptions or transformation that may change the physical behavior of the problem using the iteration of the correction functional. For nonlinear equations that arise frequently to express nonlinear phenomenon, the variational iteration method facilitates the com- putational work and gives the solution rapidly if compared with Adomian method [2]. The modified variational iteration method is remarkably effective for solving various types of ODEs of distinct orders. This method is a very promoting method, which will be certainly found widely applications.

By analyz- ing the obtained results and procedures used in modified variational iteration method and variational iteration method we observed that the modified variational iteration method facilitates the computa- tional work and minimizes it and this method cancels all the unsettled term in variational iteration method, also this method is faster than variational iteration method and save time [3].This paper is an extension of the work done in (M.A. Fariborzi Araghi, S.Gholizadeh Dogaheh, Z.Sayadi, 2011) which shows a new application of MVIM and Fourier series for linear and nonlinear non-homogeneous ODEs.

The modified varitional iteration method for solving linear and nonlinear or- dinary differential equations

In the work of (M.A. Fariborzi Araghi, S.Gholizadeh Dogaheh, Z.Sayadi, 2011), the modified varitional iteration method for solving linear and nonlinear ordinary differential equations (MVIM) proposed and applied to solve many differential equations. Hence, Accordingly we have the following formula to solve linear and nonlinear ordinary differential equations.

First Order ODEs

Let us consider the first order linear ODE of a standard form

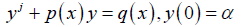                     (1)

Then the MVIM formula used to solve equation (1) is given as:

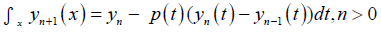                     (2)

where, 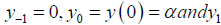is obtained from:

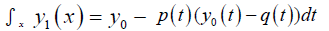                     (3)

Second Order ODEs

Let us consider the second order linear ODE of a standard form

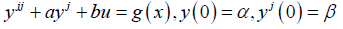                     (4)

Then the MVIM formula used to solve equation (4) is given as [2]:

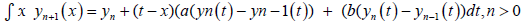                     (5)

where, 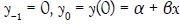and y₁ is obtained from:

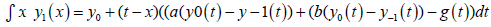                     (6)

Third Order ODEs

Let us consider the second order linear ODE of a standard form

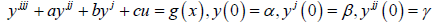                     (7)

Then the MVIM formula used to solve equation (7) is given as [2]:

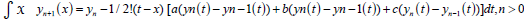                     (8)

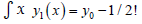
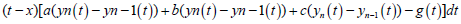                     (9)

Fourier Series of a periodic function with a period 2π

The Fourier series of a periodic functions on the symmetric interval [−π, π] is given by [4,5]:

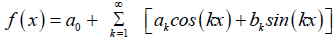                     (10)

where a0, ak and bk are called the Fourier coefficients and defined as:

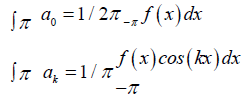
Where, k = 1, 2, 3, ...

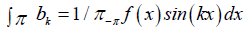
Where, k = 1, 2, 3, ...

Derivation of Modified Variational Iteration Method and Fourier series of Periodic Function with a Period 2 for Solving Non-Homogeneous Ordinary Differential Equations

Derivation for First Order ODEs

Let us consider the first order linear ODE of a standard form:

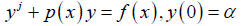                     (11)

Where f (x) is a periodic function on the symmetric interval [−π, π], such that its Fourier series ex- pansion is:

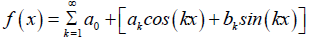
Hence, the MVIM formula used to solve equation (11) is given as [6] follows:

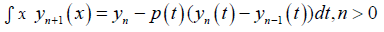                     (12)

where, y−1 = 0, y0 = y(0) = α and y1 is obtained from:

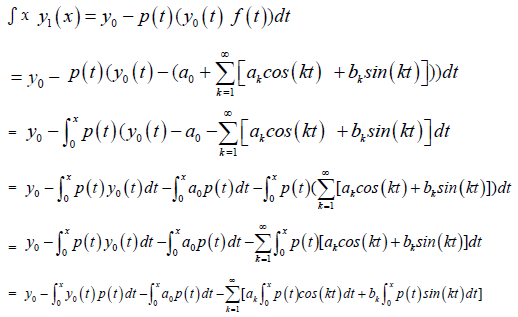                     (13)

Derivation for Second Order ODEs

Let us consider the second order linear ODE of a standard form

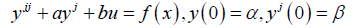                     (14)

Where f (x) is a periodic function on the symmetric interval [−π, π], such that its Fourier series ex- pansion [7] is:

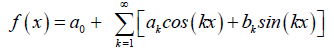
Hence, the MVIM formula used to solve equation (14) is given as follows:

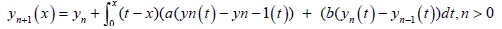                     (15)

where, y−1 = 0, y0 = y(0) = α + βx and y1 is obtained from:

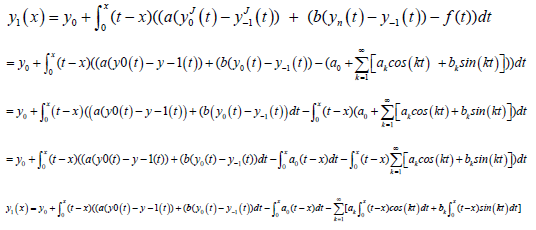                     (16)

Derivation for Third Order ODEs

Let us consider the third order linear ODE of a standard form

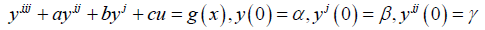                     (17)

Where f (x) is a periodic function on the symmetric interval [−π, π], such that its Fourier series ex-pansion is:

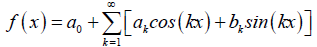
Hence, the MVIM formula [8] used to solve equation (17) is given as follows:

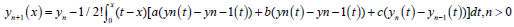                     (18)

where, 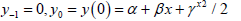and y₁ is obtained from:

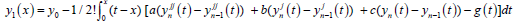                     (19)

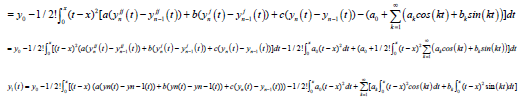                     (20)

Applications

There are non-homogeneous differential equations with a discontinuous functions,involves in the application of differential equations such as;

Steady-state damped oscillations,Rectifier and RLC-circuit in Physics [9]. Hence to solve such type of equations the modified variational iteration and

Fourier series of periodic function is one of the most powerful method.

Example 1:(Steady-state damped oscillations)

Apply MVIM and Fourier series to find the steady-state oscillations of

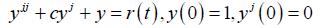                     (21)

with c > 0 and as given. Note that the spring constant is k = 1, where, r(t) is the external force depending on time t and given as follows;

r (t ) = −1 if −π < t < 0

1 if ,0 < t <π and,r (t + 2π ) = r (t )               (22)

Solution

To solve this non-homogeneous differential equation with periodic function, by modified variational iteration method and Fourier series, we first represent r(t) by a Fourier series as follows;

r (t ) = 4 / kπ sin(kt ),k =1,3,5,...

Then let set c = 1,such that equation (22) becomes;

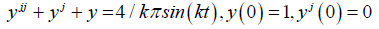                     (23)

Now, let apply MVIM and Fourier series;

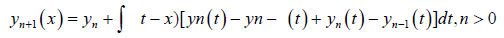                     (24)

where, y−1 = 0, y0 = 1 and y1 is obtained from:

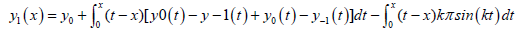                     (25)

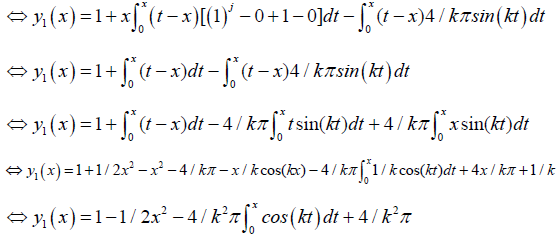
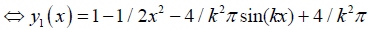                     (26)

Then, to obtain the numerical solution, we continue the iteration by substituting the value of equation (26) in to equation (24),

such that we can obtain y₂ as follows:

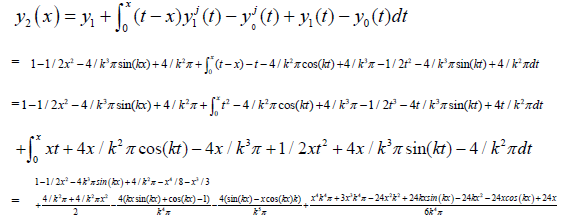
Where, k = 1, 3, 5, ..

RLC-Circuit

Apply MVIM and Fourier series to solve RLC-circuit equation.

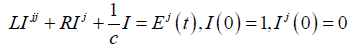                     (27)

In equation (28), find the steady-state current I(t) in the RLC-circuit, where R = 100Ω, L = 10H,C = 10−2F and E(t) as follows and periodic with period 2π, then equation (27) becomes:

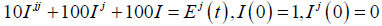                     (28)

where, E(t) is given by:

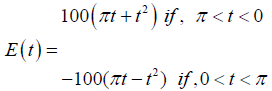                     (29)

Solution

To solve this non-homogeneous differential equation with periodic function, by modified variational iteration method and Fourier series, we first represent E(t) by a Fourier series as follows;

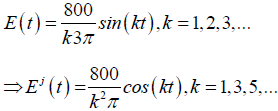
Hence equation (29) becomes;

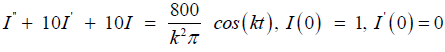                     (30)

Now, let apply MVIM and Fourier series;

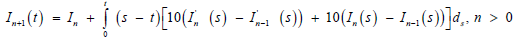                     (31)

where, I−1 = 0, I0 = 1 and I1 is obtained from:

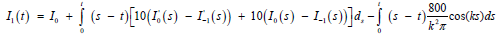                     (32)

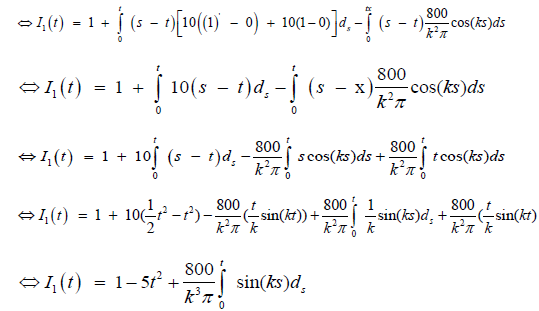
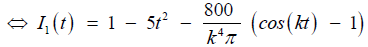                     (33)

Then, substituting the value of equation (33)in to iteration formula equation (31), we can obtain the following approximation:

Where, k = 1, 3, 5, ...Hence, for (k = 1, 3, 5, 7) the graph of I2 is given as follows;

Conclusion

In this work a formula of modified variational iteration method and Fourier series for solving linear and nonlinear non-homogeneous differential equations is derived. Particularly the method is derived and applied to non-homogeneous differential equation. If the non-homogeneous part of the Equation is non continuous periodic function with a period 2π. This new approach results is supported by investigating examples that involves non-homogeneous differential equations, such as the Steady-state damped oscillations and RLC-circuit with their graphs.

REFERENCES

1. Wazwaz AM. The variational iteration method for solving linear and nonlinear ODEs and scientific models with variable coefficients. Cent Eur J Eng 2014,4(1):64-71.
2. Benhammouda B, Vazquez-Leal H, Hernandez-Martinez L. Procedure for exact solutions of nonlinear pantograph delay differential equations. J Adv Math Comput Sci 2014, 12:2738-51.
3. Ramin H, Krishnan EN. Temperature measurement correction for the determination of the effectiveness of fixed-bed regenerators (FBRs) for HVAC applications. ASHRAE Transactions. 2020;
4. Bracewell RN, Bracewell RN. The Fourier transform and its applications. New York: McGraw-Hill; 1986.
5. Olayiwola MO. The Variational iteration method for analytic treatment of homogeneous and inhomogeneous partial differential equations. GJSFR15 (5) version. 2015;1.
6. Hilal E, Elzaki TM. Solution of nonlinear partial differential equations by new Laplace variational iteration method. J Funct Spaces 2014.
7. Mishra HK. A comparative study of variational iteration method and He-Laplace method.
8. Shang X, Han D. Application of the variational iteration method for solving nth-order integro-differential equations. J Comput. Appl Math 2010, 234(5):1442-7.
9. Salehpoor E, Jafari H, Afrapoli MA. Revised variational iteration method for solving systems of ordinary differential equations. AAM 2010, 5(3):10.