+44-7723-59-8358
The proton and neutron as distortional structures in the geometric manifold
Received: 29-Mar-2022, Manuscript No. PULJMAP-22-4607; Editor assigned: 31-Mar-2022, Pre QC No. PULJMAP-22-4607; Accepted Date: Apr 22, 2022; Reviewed: 15-Apr-2022 QC No. PULJMAP-22-4607; Revised: 15-Apr-2022, Manuscript No. PULJMAP-22-4607; Published: 22-Apr-2022, DOI: 10.37532.2022.5.2.1-5
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
The distorted-space model of matter is utilized to mimic structural elements of the proton and neutron wherein they are described as muonic-based structures. The geometrical structures are non-Newtonian in that the negativepressure core-region fields of the structure (for a positive-charge positive-shell pressure structure) do not behave functionally in an r-4 manner; the energydistribution functions terminate at zero at the radial origin (no singularity). A magnetic-field type of energy-density behavior, that is, of an r-6 behavior, at structural radial distances near the core of the distortion, is of particular interest for potential-well mimicking.
Keywords
Classical field theory; Classical mechanics; Geometry; Nuclear Physics; Structural stability
Introduction
For this Distorted-Geometry (DG) modeling, we maintain and expand the geometrical perspectives inherent in the “distorted”, or curved, geometric-space time (empty space) as the “building material of the physical world” supposition of Clifford references are cited in the text in bracketed form to distinguish from equation numbering in parentheses) [1].
Wheeler, subsequently in 1955, published his work of a similar perspective wherein, from a general relativity basis, he posited matter as a structure composed of gravitational and electromagnetic energy and he labelled his construct as “mass without mass”; he called it a “geon”[2].
At The International Congress for Logic, Methodology, and Philosophy of Science in 1960, he began by quoting William Kingdon Clifford’s “Space-Theory of Matter of 1870” and stated that the universe, from Clifford and Einstein’s view, was a geometrodynamical entity, a universe described by geometry [1-3].
A comprehensive and general treatment of the historical, geometric and physical foundations of modern geometrodynamics is found in the already cited publications of Wheeler [2,3]. Additional work in this field continues, some of which is cited in references [4-10]. The present “distorted-geometry” treatment departs from these cited “geon constructional methods” in that we do not constrain the distortional descriptions to only gravitational coupling-constant produced structures and we produce a mathematical solution to Riemann’s geometric equations to formulate a physical model for matter and energy.
The classical Riemannian four-dimensional curvature equations have been applied to describe the “localized geometrical distortions and associated energy distributions” at both quantum- and galactic-level magnitudes and radial-extensions. By requiring that the geometric distortions mimic the physical characteristics of the elementary particles, a coupling constant between energy and geometry is produced. The theoretical modeling and calculational procedure is limited to those geometric-distortional families satisfying an equation-of-state, which also expresses static, spherically-symmetric Maxwellian tensor behavior.
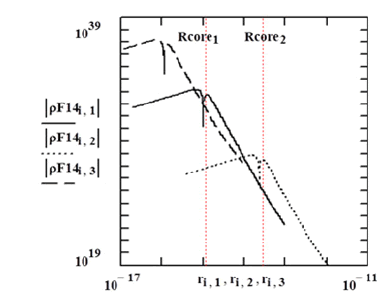
Functional solutions to Riemann’s geometric, non-linear, coupled, partial-differential equations have classically not been forthcoming. A solution however has been found for the Riemannian equation-set by describing the "distorted" space as satisfying the “equation of state”, (Equation 1). The Riemannian field equations, produced by the present “metric-solution”, (Equation 2), are of such a character that, over portions of the radial extensions of the distortion, the geometrical tensor elements exhibit negative, as well as positive, curvature-magnitudes and energy-densities. The field-observable in the negative energy-density (negative pressure) spatial region (the core region) is non-coulombic and non-infinite at the radial origin. Mass,electric charge and magnetic moments have been simulated for the down-quark, up-quark, electron, tauon, muon and neutrino as well as for a hypothetical beta-decay transition-mediating distortion-particle; this process also generates a geometric expression for the Fermi constant and conversely predicts a mass-value for the W-boson calculated to the precision of the electron g-factor (gyromagnetic ratio) [11]. Figure 1 displays the field energy-density quantities for three of these particle structures [12,13].
Figure 1: Electric-Field energy-density distribution function for distortion-1 = down quark (mass-energy = 9.269 me*c2), distortion-2 = electron and distortion_3 = muon (mass-energy = 206.768 me*c2) where ?F14 = Fd142 (see Equations 12-15); logarithmic ordinate in J/m3 units and logarithmic abscissa in meters
The dependence of the field quantities on mass-energy and electric-charge is apparent in the Figure. The field energy-density magnitudes should be compared with the experimental data in references [14-16].
By incorporating gravitational-field structures into the geometric modeling and simulation process, a refined coupling-constant is engendered. This process recovers the gravitational coupling-constant of general relativity and leads to a structural description of gravitational-like geometric-distortions.
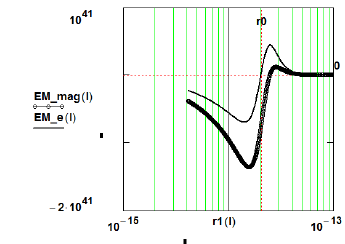
We showed in that the propagation velocity in the core region (negative pressure core for a positive-charge, positive-pressure (at large-r) structure) of these Distorted-Geometry (DG) structures was approximately 1.5 times that external to the core; see Figure 2. This feature, which is a fundamental attribute of such structures, is equivalent to a “partial light trapping” phenomenon and for gravitational structures would be classically associated with “black holes” [11].
Figure 2: Metrics and propagation-velocity factor for an electron structure; uoo=1.27394
A “geometric maximum-energy-density” feature was successfully exploited to geometrically explain and quantify the Fermi constant; in addition, a “stability-based minimum-energy-density” condition was fundamental to describing the structure of the “stable DG electron” feature. Energy-densities are equivalent to pressures and the core and shell regions of the structure hold the system in stable equilibrium. Figure 3 graphically displays such structures [11].
Figure 3: Mass-Energy-Density distribution-function surface-plots (two views) (linear radii and logarithmic amplitudes) for the geometric electron distortion
In the perspective of the DG model is a departure from the classical geometry model where the Einstein Curvature-tensor is the stress-energy-tensor describing the “material contents” of the energy distribution. The DG model is rather viewed with the energy-content residing in the warping or distorting of the manifold and therefore in its geometric-tensors, and the “curved empty space” referred to above is a “localized curved or distorted space” devoid of an “external or foreign” causative matter-entity [11].
Theoretical Foundation
A “constitutive relation” or “equation-of-state” was used as descriptive of the distorted-space volume (the physical spatial volume encompassing the distortion-produced energy), that is,
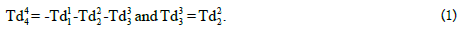
This description, Equation 1, of the distorted-space volume, has led to the universal structural solution, Equation 2, (see equations (5)-(9) for variable definitions) for the fundamental Riemann geometric-equation-set, equations [4].
where the metric quantities
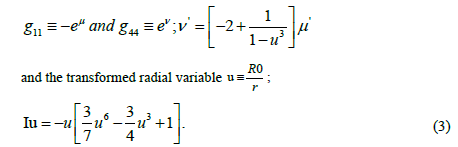
Riemann’s geometric equations (Tolman), presented here as equations (4), are expressed in the metric-variables μ' and ν' and the manifestation of the composite coupling-constant appears in the geometric quantities γ and the geometric “transformation radius” R0, both determined from the “distorted spatial volume” with electromagnetic and/or gravitational energy-density components [13].
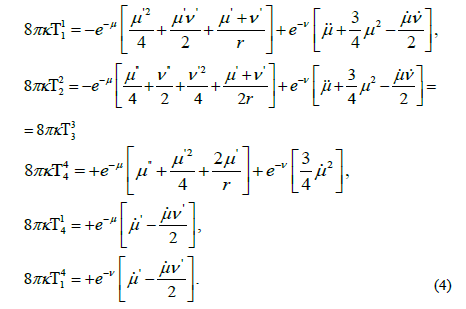
While the “energy-density Equation-of-state”, equation (1), is equivalent to Maxwell’s “energy-density” form for static, spherically-symmetric Maxwellian tensor behavior, the field equations, in both the EM realm and the gravitational realm (Q=0), exhibit r-6 geometric, static, spherically-symmetric Maxwellian tensor behavior which we have interpreted as constituting a “magnetic monopole” mimic (what is a “magnetic monopole”?) [11-13].
Building on the earlier work, we apply the geometric concepts to produce a proton- and neutron-conglomerate of distortional-geometric muon-mimics [11,12].
This section is a brief summary of the development in and is included here as a less cumbersome introduction or reference to the theoretical modeling concepts [11].
Symbols are
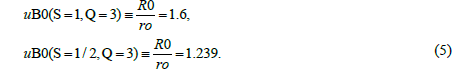
R0 is the geometric transformation radius (R0electron is calculated from the fundamental-particle magnetic-field component) and ro is the radial value at which the energy-density distribution-function transitions from the core-value to its negative in the shell (r→∞) region; ro ≡ R0/uo follows from solution for the uo roots of the field equations (6)
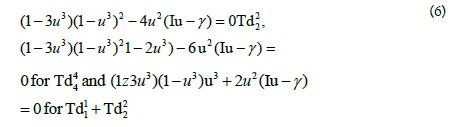
The symbolism TdXX ≡ TdXX is introduced only to emphasize the geometric character of these “distorted geometry” tensor variables.
We also define
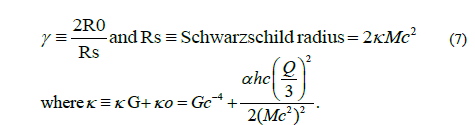
For the electron we write (me ≡ mass electron, 
= 3),
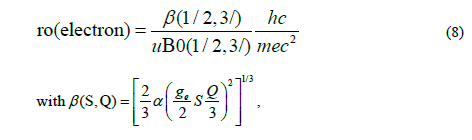
α = fine structure constant, S is the spin quantity and ge is the gyromagnetic ratio factor. Then,
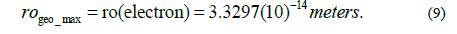
The core-radii for the EM structures are inversely proportional to the mass-energy of the distorted-geometry-structures and therefore it follows that the ro radius for the muon, or anti-muon, is
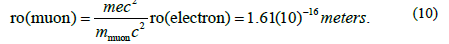
In the earlier development [11] for the geometric Fermi-constant,
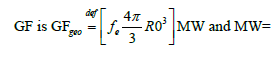
mass-energy of the W-boson. The quantity,
was originally introduced as a volume-adjustment-factor in this derivation.
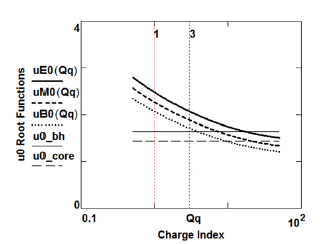
The uo root values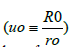 
for determining ro values, from equations (6), are plotted in Figure 4.
Figure 4: Radial-zero functions u0 (from equations (6) relative to electric-charge values; uE0 for the electrical Td2 2 function, uM0 for the mass-energy-density Td4 4 function and uB0 for the magnetic-energy-density Td1 1 + Td2 2 function. Abscissa charge-values are displayed as a function of the index Qq. uo (Qq) is graphically used for the zero-radial-function uo. Also indicated is the E_field quantity, u0_ core = uE0 (Qq= 0), and a gravitational “black-hole u0_bh” value.
The radial zero of the gravitational field quantities expressed in equations (6) is u (ro) = 3.27512/2 if ro = Rsgeo. Rsgeo = R0geo/u (ro) is the geometric manifestation of the Schwarzschild “metric-radial-zero”, the radial singularity classically interpreted as a “black-hole” radius.
The Riemannian geometric field equations follow from equation (4) and are taken from [13] according to Tolman;
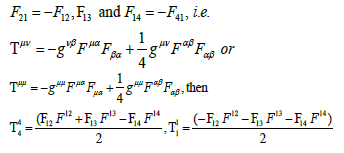
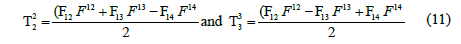
The resultant field quantities are
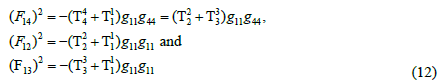
Therefore, we see that the static-spherically-symmetric Maxwellian tensors exhibit the same stress and energy relationship as the geometric tensors.
Finally, it is of interest to examine the ratio of the 1/r6 tensor-component to the 1/r4 tensor-component in the construction of the geometric fields. The geometric-energy-density or field equations are
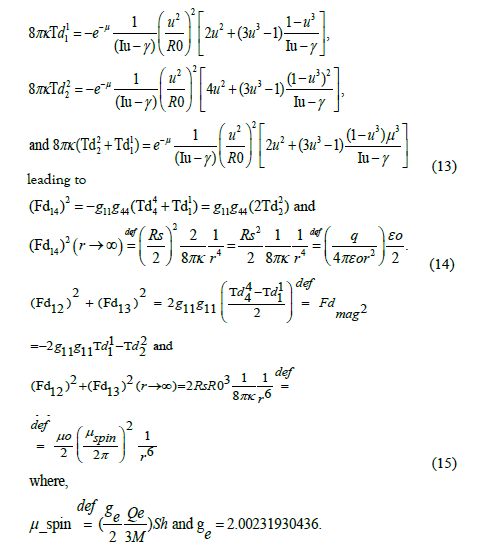
In discussions of the negative energy-density (pressure) core-regions of this universal (EM as well as gravitational) distorted-geometry structure, it should be emphasized that a negative energy-density gravitational feature (a repulsive gravitational force or negative pressure) is non-Newtonian. The hole or core region-fields of the structure are repulsive thereby stabilizing the structure, do not behave functionally in an r-4 manner and terminate at zero at the radial origin (no singularity) [13]. This field behavior is a fundamental feature of these “distorted-space” structures; the field exhibits r-4, r-6 and r-n dependences in both the core and shell regions and is thereby able to account for “Newtonian” “weak”- and “strong-fields” (see equations (14, 15).
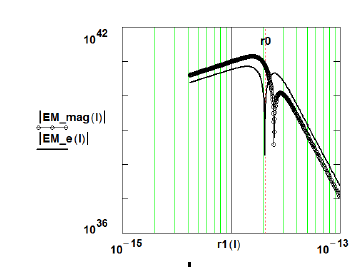
To further illustrate the structural character of the “distortional-geometry mimics”, we compare at “near-core radial regions” the geometrostatic field quantities Fd142and Fdmag2 which are also the geometric mimics of the Maxwellian tensors. For both gravitational and electromagnetic distortions, the magnetic field component, Fdmag2, is non-zero at the “radial field zero”, Fd142=0, or “core radius (ro)” (in the gravitational realm, this field feature would seem responsible for accretion-disk and galaxy-matter rotational-distribution behavior). Figures 5 and 6 are constructed for the “distorted-space electron-mimic” although the energy-density distribution functions are qualitatively similar in the normalized radial variable u=R0/r. The Figures are meant to more dramatically illustrate the magnitude of the structure’s magnetic energy-density component vs the Fd142 energy-density component.
Figure 5: Field-Energy-Density distribution-functions; radii (logarithmic in meters) and amplitudes (logarithmic in joules/m3) for the DG geometric electron-distortions
Figure 6: Field-Energy-Density distribution-functions; radii (logarithmic in meters) and amplitudes (linear in joules/m3) for the DG_geometric electron-distortions
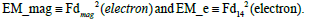
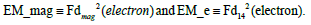
Actually, the (Fd14)2 fields contain r-6 elements of a magnitude comparable to the magnetic-field strengths (Fdmag)2 resulting in a significant departure from the classical Newtonian r-4 (or r-6) behavior. The fields also exhibit potential-well behavior as they radially (shell values) transition to repulsion (if attractive in the shell) at the hole-core radius ro.
Methods For Proton And Neutron Modeling
We use the following experimental data to generate and illustrate the model parameters:
Mass energy of proton (Mp) = 938.2716 MeV, electric charge of proton (Qp)= +e and gyromagnetic ratio (g-factor) of proton (gp)= 5.585694; mass energy of neutron (Mn)=939.564 MeV, electric charge of neutron (Qn)=0, gyromagnetic ratio (g-factor) of neutron (gn)= -3.826085;
mass energy of muon (Mμ) = 105.658 MeV, electric charge of muon (Qμ) = -e, gyromagnetic ratio (g-factor) of muon (gμ) = -2.002331, and
mass-energy of anti-muon (Maμ) = 105.658 MeV=Mμ, electric charge of anti-muon (Qaμ)= +e and gyromagnetic ratio (g-factor) of anti-muon (gaμ)= 2.002331 [14-16].
The electron characteristics are:
mass energy of electron (me*c2) = 0.510998 MeV, electric charge of electron (Qe) = -e, gyromagnetic ratio (g-factor) of electron (ge) = -2.002319.
Calculating the binding energy of the proton, modeled as a structure of 4 muons and 5 anti-muons (the matter-antimatter asymmetry problem?), we get BEp (binding energy of proton) ≡ 9 Mμ–Mp = 12.6504 MeV. Similarly, the binding energy of the neutron ≡ Ben = 9 Mμ + Me–Mn = 11.358 MeV. The muons and anti-muons are posited to coexist within the immediate field environment of the composite structure as, for example, neutrons existing within elemental structures, or, in other field-induced structural modifications. For comparison to other nuclear structures, a binding energy per nucleon, where a “nucleon” definition here incorporates the muon, is BEp_μ = 1.40555 MeV/nucleon and Ben_μ=1.318666 MeV/nucleon [15,16].
For the DG_mimicked-proton, the electric-field is that of an anti-muon (the other 4 muon/anti-muon pairs exhibiting zero-charge or self-neutralization and zero g-factors). The g-factor value of the 4th muon is field “flipped” and a resultant sub-structure of two anti-muons and the “flipped” muon-produces a “field induced” composite g-factor, reduced from the free-field value of (2.002331) per anti-muon to (1.861898) per anti-muon, to create a proton g-factor of (5.585694). The proton (stacked-muon) radius, assuming a 3-layer, 3 muon/layer, @ 4 ro-muon separation (center to center) between muons, in a stacked-geometry-configuration, would be approximately 10 ro_muon or 1.0625(10)-15 meters [16].
For the DG-mimicked-neutron, which is here posited as a DG-mimicked proton surrounded by a DG-mimicked electron (ge = -2.002319), the simplest formation structure would be that of field “flipping” the g-factor of one DG-proton-anti-muon from (+2.002331) to (-2.002331) with a field induced reduction to (-1.823766). The resultant neutron g-factor would then be (-1.823766) + (-2.002319) = (-3.826085) (Figure 6).
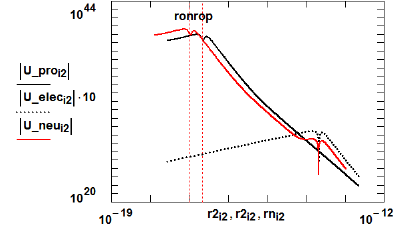
For this DG_mimicked-neutron, the electric-field is that of the DG_mimicked core-proton plus the field of the shroud DG_mimicked electron registered on the same center as the protonic-core (see Fig.7). In other words, a zero-charge field (at large radii) but a “DG-field” near and within the ro (electron) radius. The neutron ro radius is that of the shroud-electron-mimic or ro(neutron) = ro(shroud-electron) =2.197(10)-14 meters.
The energy-density features of these structures are illustrated in (Figure 7). The field-energy-density distribution functions are recast as, For example,
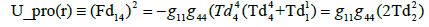
and the neutron distribution is defined as
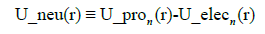
where the “n” subscript denotes the impact of the gyromagnetic factor ge. The DG_proton g-factor produces U_pro(r) + U_elec(r) and the DG_neutron g-factor produces U_pron(r) + U_elecn(r). Absolute values are displayed because of the energy-density-value transition at the core radii.
Figure 7: Field-Energy-Density distribution-functions; radii (logarithmic in meters) and amplitudes (logarithmic in joules/m3) for the DG_geometric distortions
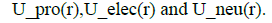
The symbols ron and rop are the DG_neutron and DG_proton core radii.
Some experimental data have been measured for the proton and are detailed in reference as:
“The proton, one of the components of atomic nuclei, is composed of fundamental particles called quarks and gluons. Gluons are the carriers of the force that binds quarks together, and free quarks are never found in isolation-that is, they are confined within the composite particles in which they reside [17]. The origin of quark confinement is one of the most important questions in modern particle and nuclear physics because confinement is at the core of what makes the proton a stable particle and thus provides stability to the Universe. The internal quark structure of the proton is revealed by deeply virtual Compton scattering, a process in which electrons are scattered off quarks inside the protons, which subsequently emit high-energy photons, which are detected in coincidence with the scattered electrons and recoil protons. Here we report a measurement of the pressure distribution experienced by the quarks in the proton. We find a strong repulsive pressure near the centre of the proton (up to 0.6 femtometres) and a binding pressure at greater distances. The average peak pressure near the centre is about 1035 Pascal’s (Joule/m3), which exceeds the pressure estimated for the most densely packed known objects in the Universe, neutron stars.
This work opens up a new area of research on the fundamental gravitational properties of protons, neutrons and nuclei, which can provide access to their physical radii, the internal shear forces acting on the quarks and their pressure distributions.”
In the DG_neutron, the core values of the DG energy density distribution for the co-centered electron are of the same sign as the energy-density shell values of the protonic-muon structures but of an almost infinitesimal value compared to the muonic values. At the electron-core radius the two energy density distributions are of opposite magnitudes and produce a composite neutral charge character (Qneu=0) (for radii greater than ro (electron)) and the modified g-factors discussed above.
Conclusion
It has been shown in the present work that the distorted-space, or Distorted Geometry (DG), model of matter, as applied to fundamental-particle (muon/anti-muon) constructs, can mimic the composite neutron and proton structures. Such structural content thereby also resolves the heretofore “matter-antimatter asymmetry problem”. The distorted-geometry structures exhibit non-Newtonian features wherein the core-region and shell-region fields of the structures do not behave functionally in an r-4 manner and terminate at zero at the radial origin (no singularity). This field behavior is a fundamental feature of these “distorted-space” structures; the field behavior exhibits r-4, r-6 and other r-n dependence in both the core and shell regions and is thereby able to account for, explain and mathematically elucidate “Newtonian”-, “weak”- and “strong”-fields”.
REFERENCES
- Clifford WK. On the space-theory of matter. In the concepts of space and time. Springer Dordr. 1976;22:295–296.
- Wheeler JA. Geons. Phys Rev. 1955 15;97(2):511.
- Wheeler J. A., Logic, methodology, and philosophy of science, Proc. 1960 International Congress, USA. Stanf Univ Press, 1962;.361.
- Ciufolini I, Wheeler JA. Book Review: Gravitation and inertia/Princeton U Press, 1995. The Observatory. 1996;116:250.
- Koehler DR. The proton and neutron as distortional structures in the geometric manifold. Phys Rev 1997; 4824-33
- Perry GP, Cooperstock FI, Stability of gravitational and electromagnetic geons. Class Quant Grav 1999;16:40.
[Google Scholar] [Crossref].
- Sones RA. Quantum geons. arXiv preprint gr-qc, 2005;2:0506011.
- Stevens KA, Schleich K, Witt DM. Non-existence of asymptotically flat geons in (2+1) gravity. Class Quantum Gravity. 2009 19;26(7):075012.
- Vollick DN. Addendum to ‘Gravitational geons in 1+ 1 dimensions’. Class Quantum Gravity. 2010 7;27(16):169701.
- Louko J. Geon black holes and quantum field theory. J Phys Conf Ser 2010; 222(1): 012038.
- Koehler DR. Geometric-distortions and physical structure modeling. In J Phy. 2013;87(10):1029-34.
- Koehler DR. The proton and neutron as distortional structures in the geometric manifold. Reasearch Square. 2021.
- Tolman RC. Relativity, thermodynamics, and cosmology. Courier Corporation. 1987; 258.
- 2018 CODATA Value: electron mass in u. NIST 2019.
- Gell Y, Lichtenberg DB. Quark model and the magnetic moments of proton and neutron. 1969 ;61(1):27-40..
- Alvarez LW, Bloch F. A quantitative determination of the neutron moment in absolute nuclear magnetons. Phys Rev 1940 15;57(2):111.
- Burkert VD, Elouadrhiri L, Girod FX. The pressure distribution inside the proton. Nature. 2018 ;557(7705):396-9.
