The Self-Interaction Field Theory Part I: Scalar theory and its application in astrophysics
Received: 10-Nov-2024, Manuscript No. PULJMAP-24-7270; Editor assigned: 12-Nov-2024, Pre QC No. PULJMAP-24-7270 (PQ); Accepted Date: Nov 26, 2024; Reviewed: 18-Nov-2024 QC No. PULJMAP-24-7270; Revised: 24-Nov-2024, Manuscript No. PULJMAP-24-7270 (R); Published: 28-Nov-2024
Citation: Pan Q. The Self-Interaction Field Theory Part I: Scalar Theory and its application in astrophysics. J Mod Appl Phys 2024;7(4):1-11.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
Through revisiting Einstein’s General Relativity, it is discovered that the mesons mediating the Einstein’s gravitation travels in a unique space time different from photon space time because photon can be trapped in a blackhole, and mesons mediated the gravitations cannot. Two assumptions are proposed to make Newton’s gravity and Einstein’s gravity consistent to each other in the classic physics domain. The assumptions require the gravitational field to be self-interacting so that the mesons mediating the gravitation can also be trapped. A classical Lagrangian of scalar field with self-interaction property is proposed. The non-linear term is from the requirement of field self-energy-momentum as also part of source of the field. If the field is strong enough, the field or the mesons mediating the field itself will be trapped which forms the boundary of field and the object. Due to the field self-interaction, the field will be focused by the asymmetric matter distribution. The characteristics of 3-Dimension, 2- Dimension and 1-Dimension confinement of the field is discussed. The strong Self-interaction constant and gravitational constant are related to each other by ratio of the observable universe radius to the nuclei radius, or the Dirac Large Number 1039. The purpose of this theory is to unify the strong interaction, quantum interaction and gravitation together. Part I of this series of papers is about the assumptions, scalar theory, and its application in Astrophysics. Part II is about applying the theory to quantum mechanics, strong interaction, and the relationship between different physics constants. Part III is the tensor version of the Self-Interaction field theory.
Keywords
Self-interaction field; Dirac large number principle; Gravitational constant; Binary stars; Kuiper belt; Youth paradox
Introduction
Einstein’s field equations are the special relativity extension of Newton’s law of gravity. Newton’s law of gravity is only tested in our local solar system which is dominantly the solar mass. On a large scale, the rotation curve of our solar system around the galaxies is different from what derived from Newton’s law of gravity based on the observable mass. One solution to this discrepancy is to add dark matter to the galaxy. Another approach is to modify Newton’s Law of gravity. The theory to be proposed here is to modify Newton’s Law of Gravity. Einstein’s General Relativity (GR) contains two parts: One part is the weak equivalence principle which embeds gravitation into a curved space-time. Through the weak equivalence principle, the particles motion in curved space time is described through local affine connections. The second part of GR is Einstein’s field equations which prescribes how energy-momentum and boundary conditions determine the curvature of space time.
The weak equivalence principle and weak field limit of Einstein’s field equations are being well tested. But in the strong field limit, both Newton’s law of gravity and Einstein’s field equations have not been fully tested. In the theory of general relativity, there are blackholes. If we keep the philosophy that all interactions are contact interactions. For contact interaction reason, physicist created field. The first demonstration of the field is the iron powder near the magnet form the pattern of field. If general relativity is correct, field or the Mesons Mediating the Gravitations (MMG) will have to get out of blackholes to attract other matters outside of blackhole. Thus, Einstein’s general relativity put gravitational field or MMG in a unique position that field does not follow the curved space time the field creates. There is another option that if field also travels in the curved space time, field must interact with fields itself. This self-interacting field theory will be derived from the concept of how matter interacts with field where the matter energy-momentum is replaced by the field energy-momentum.
In modern field theory, the field is mediated by mesons including relativity gravitons for gravitation. Einstein’s general relativity gives gravitons a unique path to travel which is different from photons. As a matter of fact, if gravitons travel like photons, there will be no gravitons outside of the black hole event horizon. Obviously, this is not the case for Einstein’s general relativity. In this paper, the term Mesons Mediating Gravitation (MMG) is used to avoid confusion between the mesons defined in this paper and Einstein’s gravitons.
The field equations of General Relativity are derived from the Lagrangian of second order derivative of field variables g_αβ while other field theories are derived from the Lagrangian having first order derivative of field variables. Another issue with Einstein’s field equations is that the affine connection which is related to acceleration is not a tensor. These two questions will be further discussed in Part III.
If we bring physics back to the early 1900’s, our intuition is that the field strength shall be proportional to the field lines. The origin of the 1/r2 term in Newton’s law of gravity and electro-magnetic field comes from the surface density of field lines. The current paper is to explore the semi-classic theory of gravitation based on the assumption that combines the theory of classic field strength being proportional to the surface density of field lines and the assumption that mesons mediating the gravitation travelling like photons in space time. This series of papers contains three parts: this current paper is about the assumptions and theory itself and its application in Astrophysics. Part II is about applying the theory to quantum mechanics, and strong interaction. Part III is the tensor version of this self-interaction field theory in which Einstein’s general relativity is rewritten to accommodate the assumptions proposed in this paper.
The assumptions of the theory
Einstein’s weak equivalent principle is based on the equivalence of the mass of gravitation mg to the mass of inertia mi in Newton’s law of gravitation. Thus,
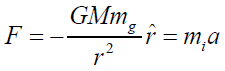
can be rewritten as following in considering of mi = mg:

where ř is the unit vector in the direction of r.
The general theory of relativity
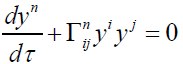
states that all particles, regardless of mass of particles, follow the same space time if the initial conditions are the same because 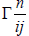 is independent ofmass and nature of test particles without considering other interactions.
is independent ofmass and nature of test particles without considering other interactions.
Another key variable of above Eq. (1) is 1/r2, where the 2 is exactly 2, not 1.9 or 2.1. Newton’s Law of gravity indicates that the 1/r2 represents the surface density of the field lines in classic physics. In classic physics domain, rewrite equation (1) as

where σs is the surface number density of the Mesons Mediating The Gravitational field (MMG) (or field) created by unit mass.
Considering the speed of gravitation field (or MMG) is constant, Equation (2) can be rewritten as
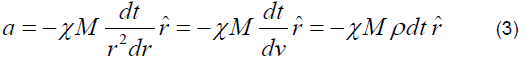
where ρ is the number density of the MMG per unit mass passing by aspace point dv times the interaction time and χ is the proportionalconstant. If the Mesons Mediating Gravitation (MMG) behaves like other particles in gravitational field, Newton’s law of gravity needs to be modified in order to accommodate equation (3). In this paper a non-Newtonian theory of gravity is proposed based on the following assumptions.
Assumptions:
1). The mesons Mediate Gravitational Field (MMG) travel in space time like all other particles in gravitational field.
2). And the classic gravitational acceleration of any particle in gravitational field is proportional to the local number of mesons mediating the gravitation passing by the space point times the interaction time.
In this paper, the Einstein’s general relativity theory is used to do analysis of the MMG behavior in the space time as the first order approximation to the Self-Interaction Field theory we are proposing in this series of papers before the full Self-Interaction field theory is developed. The above Assumptions lead to the difference between this theory and classic Newton’s Law of Gravity in the following three cases:
1). Non-symmetric mass distribution systems because MMG can be focused by mass along it way and σs is different in different direction even theradial distance is the same.
2). In strong field limit, MMG can be slowed down or even trapped by strong field and the local density increases as the field strength increases.
3). The source is rotating where the MMG radial speed is slower due to inertial frame rotation. In the weak field limit and spherical system σs in our theory shall not be so much different from the classic Newton’s law of gravity. In the solar system, all the tests related to Newton’s law of gravity shall be true except if the planet is in the shadow of another planet.
When the field is strong, like the “black hole” of general relativity, no particles escape from the “black hole” and the photon is infinitely red shifted and trapped inside the black hole, no MMG escape from the “black hole”, and a = 0 outside of a “black hole” based on equation (3). Inside the “black hole”, for the ingoing MMG is infinitely violet shifted, a goes to infinite. The Schwarzschild “black hole” is not black, but does not interact with surrounding matters based on the assumption. Rewrite the number density in equation (3) as following based on the definition of number density:

Where  is the frequency which defines the mesons bounce back and forth, σs is the surface density, y s is the classic speed of MMG in thedirection S normalized by c and R is the bounce back (or trapped) radius of the MMG. Putting Equation (4) back into (3),
is the frequency which defines the mesons bounce back and forth, σs is the surface density, y s is the classic speed of MMG in thedirection S normalized by c and R is the bounce back (or trapped) radius of the MMG. Putting Equation (4) back into (3),

In the case of Einstein’s gravitons and the electromagnetic fields, ys isclose to 1 and it is the speed of MMG in the direction of σs ComparingEquation (5) with (2), the Newtonian gravitational constant 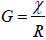
The gravitational constant is inversely proportional to the bound radius of the system which is the same as Dirac’s large number principle [1]. This will be further analyzed in the future parts of this series of papers. Based on the assumptions, besides the particles, the field will also be trapped when the escape velocity is equal to the speed of light. The field can be trapped in 3-sphere through self-interaction when the amount of matter is large enough, or matter is dense enough. The field can be bent and focused, which means it can be trapped in 1-d as a string or 2-d as a disk. Part II and Part III of this theory, the universe, nuclei, photon, electron are all assumed to be the self-interaction field-bounded particles with the generating source of field being energy momentum. The general relativity introduced the self-interaction between fields which are non-linear. The question now is that if the classic field are also self-interacting, what would be the field equation look like? In Section 3, the implications of the assumptions are further discussed. In section 4 of this paper, two types of Lagrangian for the self-interacting scalar fields with energy momentum as the source of the field are introduced. In section 5, the meaning of the extra term from the SI Lagrangian is discussed. It is clear this extra term determines how the field is bent or focused. In section 6, How the field is trapped in 3-diemsion space, 2-dimension space and 1-dimension space are discussed. In Section 7, the weak observable effects of the self-interacting terms in the galaxy and solar system are discussed.
Implications of the assumptions in physics
Variation of Einstein’s field equation in radical direction: Assuming the field travels in space-time like other zero mass and the field density times the interaction time determines the acceleration. Einstein’s filed equations are the special relativity extension of Newton’s Law of Gravity. From the analysis of congruence of null geodesics in the radical, null geodesics of Schwarzschild space-time is considered with dθ = dϕ = 0. TheSchwarzschild line element reduces to
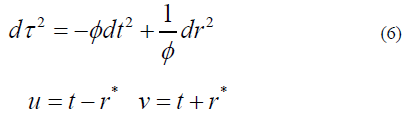
Where 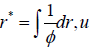 constant defines outgoing null geodesics, while v = Constant defines ingoing null geodesics.
constant defines outgoing null geodesics, while v = Constant defines ingoing null geodesics.
The vector field defined by

are null and they both satisfy the geodesic equations.
The congruence defined by 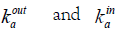 are clearly hypersurface orthogonal. Their expansions defined by Raychaudhuri’s equation are
are clearly hypersurface orthogonal. Their expansions defined by Raychaudhuri’s equation are
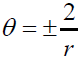
θ is the fractional rate of change of the congruence’s cross-sectional area:

Where δA is measured in the purely transverse directions. From (7), it isclear that Schwarzschild spacetime expansion is the same as that of the flat spacetime.
The equation of motion for zero mass particles in the radial direction is,
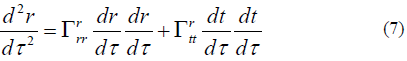
If we eliminate of the Eq. (7), the equation become

This is the Newton’s law of gravity except the extra factor . When is near the boundary of black hole, the gravitational force is zero for the null geodesic. But this is different from the assumption of SI field theory proposed by the author. Because
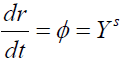
Where Ys is the speed defined in Equation (4). And if φ is less than thespeed of light, the field has more time to interact with the particles, the strength of the gravitation in related to the radial direction is inversely proportional to φ like in the equation (4), thus the following

is a reasonable assumption if Newton’s law of gravity needs to be modified based on the assumptions? Eq. (9) has two solutions for φc

For the case, 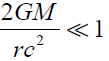

And

φc1 is the Schwarzschild solutions with potential as 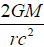 Rewrite φc2 as
Rewrite φc2 as
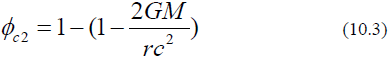
φc2 is a different solution from Schwarzschild solutions with potential as
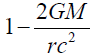
If in the term 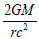 mass and the radius are the nucleon’s mass and radius and G is the gravitational constant, the potential of is of φc1 is 10-39 φc2 which is also very close to Dirac Large number hypothesis [1]. Another feature of this equation is that if
mass and the radius are the nucleon’s mass and radius and G is the gravitational constant, the potential of is of φc1 is 10-39 φc2 which is also very close to Dirac Large number hypothesis [1]. Another feature of this equation is that if 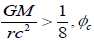 will be complex. We will come back to discuss this complex space time in a future paper regarding quantum mechanics. Rewrite Eq (9) into
will be complex. We will come back to discuss this complex space time in a future paper regarding quantum mechanics. Rewrite Eq (9) into
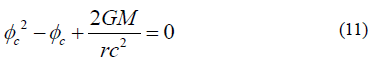
take the Laplace operator on Eq (11) lead to
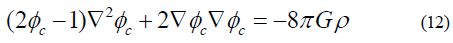
Eq (12) is the self-interacting field equations with ∇φc∇ φcas the field energy density source for generating its own gravitational field. From this analysis we see that the assumption led to the field to be a self-interaction field of Equation (12).
Field or mesons mediating the field bounce back and forth: The traditional Gaussian law of gravity does not assume the field to bounce back and forth. But the modern QED allows the virtual particles to be emitted and re-absorbed. Equation (4) indicates that gravitational constant is inversely proportional to the field bound radius R.
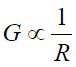
If the strong self-interaction constant sG is also part of this assumption,then
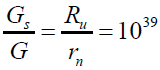
where Ru is the radius of the observable universe and rn is the nucleonsradius. From this analysis and section 3.1, both give the same Dirac large number [1]. It may indicate that this self-interaction field theory may lead to the unification of strong interaction and gravitation. I tis interesting that both analysis of section 3.1 and 3.2 give the same large number.
The self-interacting Lagrangian and its Euler equation
Einstein’s field equations:
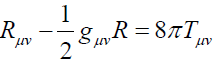
Where
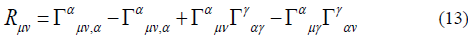
The ΓΓ terms are self-interaction terms. What is the classical scalar model for this kind of self-interaction term?
The Newton’s Lagrangian for gravitation
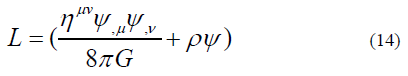
And the Hamiltonian is
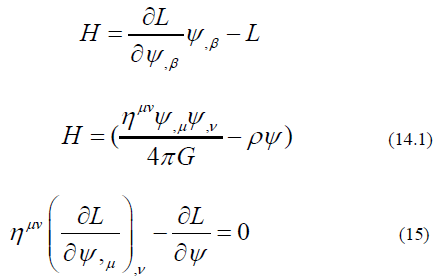
The first term of Eq. (15) is the flux term of the field like the flux term in hydrodynamics and the second term is the source term. If the field is self-interacting, the source term shall be proportion to the energy density of the field itself. That is:

Where Tμv is the energy momentum density of the field, not including the matter. Eq. (16) is an important equation to find the self-interacting field equations with energy momentum as the source of the field.
Considering that in the Lagrangian of Newtonian gravity, matter-field interaction term is ρψ, and in the Maxwell equation, the charge-field interaction term is AμJμ. The self-interacting (Scalar Field-Field Interaction) term shall be ημvψψ, μψ,ν .
The typical self-interaction Lagrangian: Let us look into the scalar field of the Lagrangian which has the property of Eq. (16)

where a constant ϕ0 is introduced to normalize ϕ so that ϕ/ ϕ0 has no nuvϕ, u ϕ, v dimension. Now ϕ has the dimension of kg/m (mass over length).'sϕ dimension of kg/m makes ημvϕ,μϕ,v having the same dimension a ρϕ.
The Hamiltonian of Lagrangian (17) is
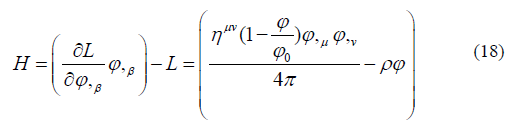
This Hamiltonian after normalized by ϕ0(=H/ϕ0) has only the field energy and the interaction between matter and field. It does not include the matter energy itself. The field-field interaction energy-momentum (only field) is:
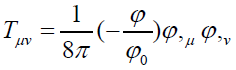
It is clear that Lagrangian like Eq. (17) meets the requirement of Eq. (16) because
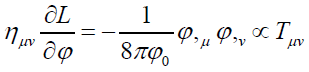
The Euler equation of Equation (17) is
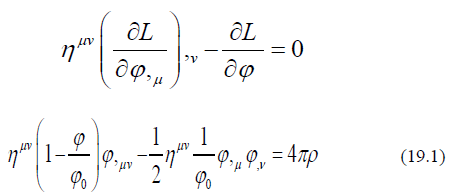
If ϕ0 is divided on both sides of Eq. (19.1), and replace 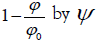
Equation (19.1) becomes
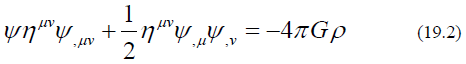
Where G is a constant defined as 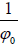
Take the derivative of ημv on both side of equation (19.2) gives the tensor format of equation this self-interaction field theory.
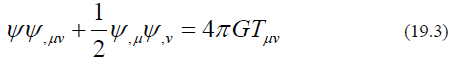
Equation (19.3) does not include the metric tensor field yet. It will be interesting to include the metric tensor in the Lagrangian which will be further discussed in Part III of this serial of papers. Please note that this Tμv is not the energy momentum defined in Einstein’s General Relativity. Analysis of Equation (19.1) and (19.2) gives very interesting results which match our assumption defined in Section 2. From Equation (19.1), near the boundary 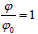 or ψ =0, The first term of Equation (19.2) is zero, if there is no mass right outside of the boundary ψ, μ = 0 or ψ =constant which can be chosen to be 1. It means that outside of the “blackhole”, the space time is flat. In section 5, we will see that Equation (19.2) causes the field to be bent by the neighboring mass which is our assumption 1. If ϕ0 is the maximum value of the
or ψ =0, The first term of Equation (19.2) is zero, if there is no mass right outside of the boundary ψ, μ = 0 or ψ =constant which can be chosen to be 1. It means that outside of the “blackhole”, the space time is flat. In section 5, we will see that Equation (19.2) causes the field to be bent by the neighboring mass which is our assumption 1. If ϕ0 is the maximum value of the 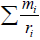 of the closed object, the inverse of the universe
of the closed object, the inverse of the universe 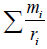 shall be Newton’s gravitational constant. If ϕ0 is very close to 1 like the
shall be Newton’s gravitational constant. If ϕ0 is very close to 1 like the 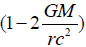 in the weak filed limit, Equation (19.2) becomes Newton’s Law of gravity with an extra term
in the weak filed limit, Equation (19.2) becomes Newton’s Law of gravity with an extra term 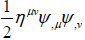 We will discuss the implication of this new term in section 5. Solving the Euler Equation (19.2) gives the value of
We will discuss the implication of this new term in section 5. Solving the Euler Equation (19.2) gives the value of 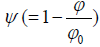 If the interaction Hamiltonian Equation (18) normalized by ϕ0 plus the mass itself is integrated over the space within the boundary, shall be equal to the total mass of the object. That is:
If the interaction Hamiltonian Equation (18) normalized by ϕ0 plus the mass itself is integrated over the space within the boundary, shall be equal to the total mass of the object. That is:
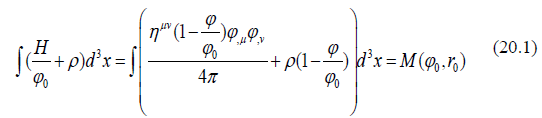
Equation (20.1) shall give a relationship that mass is a function of ϕ0 and r0 (the boundary). Another condition is that at the boundary, the escape velocity is the speed of light. From the solution of Equation (19.2) if vescape = C
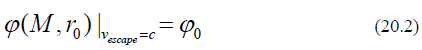
(20.1) and (20.2) will give a full property definition of total mass, the gravitational constant and its radius for a closed object (like the universe, or the nucleon). For a spherical object with constant density, the integration of Equation (20.1) gives

where β is an integration constant, which is equivalent to the condition of Schwarzschild black hole:
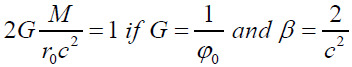
This self-interaction boundary is different from Einstein’s blackhole event horizon because outside of Einstein’s blackhole there is still attractions from the black hole, while for this self-interaction theory, there is no gravitational interaction outside of the boundary. Equation (20.3) can describe an oscillating as long as the equation holds true. If r0 increases, and M does not change, then 0ϕ becomes smaller (or G becomes larger), that means the gravitation becomes stronger which means the expansion of the object will be slowing down due to stronger gravitation. If r0 decreases, and M does not change, then ϕ0 becomes larger (or G becomes smaller), that means the gravitation becomes weaker which means the collapsing of the object will be slowing down due to weaker gravitation. This new equation (20.3) will be used to study quantum mechanics and cosmology. Solving the self-interaction field equation is much more difficult comparing with Newton’s law of gravity because of its non-linearity and also the boundary conditions is now different from classic Gaussian law of gravity:
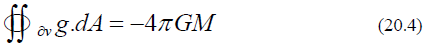
∂V is any closed surface (the boundary of an arbitrary volume V) dA is avector, whose magnitude is the area of an infinitesimal piece of the surface ∂V , and whose direction is the outward-pointing surface normal (seesurface integral for more details), g is the gravitational field, G is the universal gravitational constant, and M is the mass enclosed within the surface ∂V. The classic Gaussian law of gravity (20.4) is different fromequation (20.1) of the self-interaction Gaussian law of gravity because out of the “blackhole” surface g is zero, but there is still mass within the surface. Thus, Equation (20.1) is integrated on the boundary. Integration outside of the boundary is meaningless.
Also, in Eq. (20.1), if part of the surface is integrated, then part of the mass δm appears on the right-hand side of the equation
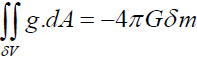
Due to the field being focused, can be zero, then g is the gravitational field can be infinite because is conserved which both Einstein’s relativity and Newton’s Law does not have this property.
The exponential self-interaction and quantum potential: Even though we use the ημvϕ,μϕ,v as the self-interaction (ψ× field energymomentum defined by ψ) term, there can be other form of self-interaction. For example, the Newtonian field co-vector ϕ,μ while thequantum potential co-vector is 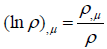
The quantum potential is
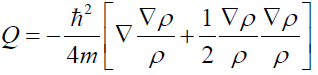
In fact, the quantum potential co-vector is normalized by the variable itself. Let’s call it the log potential co-vector (field gradient divided by the field variable itself). It is interesting that affine connection in Einstein’s general relativity is also a log potential co-tensor after some re-definition in the Tensor Self-Interaction Field Theory to be published by the author.
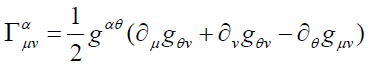
Where θ∂μgθv is normalized by gαθ
Equation (19.2) can be rewrite into the format like the quantum potential of the following:
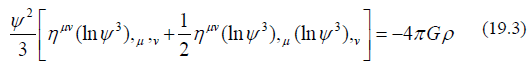
Defining ψ3 as Ψand divide both side by 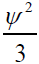 (19.3)
(19.3)
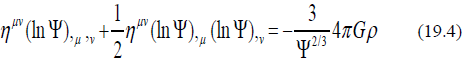
Equation (19.4) is equivalent to the quantum potential, but the interaction coefficient is infinite when Ψ goes to zero. Because Eulerequations build the relationship of field self-energy (second term) to the second order of differentiation (first term). This is why both quantum mechanics and Einstein’s general relativity has second order differentiation as part of the energy momentum of the field. Define ln ψ as the field variables, equation (19.4) can be rewritten as
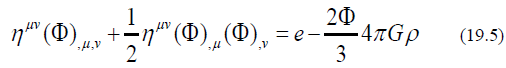
Eq (19.5) can be derived from a Lagrangian can be derived from an exponential self-interaction Lagrangian.
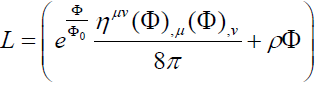
Where varies from 0 to −∞. At the boundary, Φ is −∞. Due to the exponential interaction, the field strength changes quicker near the boundary when interacting with matter. Thus, the matter is either in the boundary or out the boundary quickly.
From Equation (19.4), we see that the interaction of field times energy momentum as interaction is a typical interaction. We can also have other self-interaction types. The following is the interaction similar to MIT bag model.
The self-interaction similar to MIT bag model: Consider another Lagrangian,
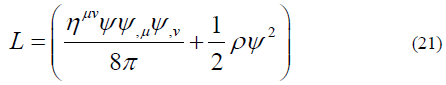
This Lagrangian (21) is different from (17) by changing the ϕ0toϕ.
The Hamiltonian corresponding to (21) is
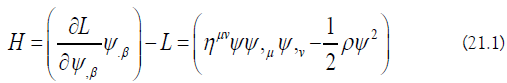
The Euler-Lagrange equations of (8) is:
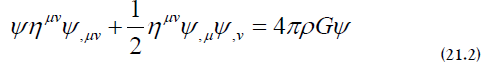
Where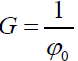
Further divide equation (21.2) by ψ, gives
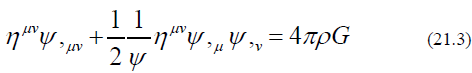
This is Newton’s Law of gravity with an extra term. If we take the notation of ψ having the largest value 1 in the center of the spherical mass distribution and become smaller and smaller to the boundary. The field is trapped when the escape velocity is the speed of light, ψ equals to zero. Thus ψis close to 1 at the center of the object and become zero at the boundary of the Einstein “Blackhole”. On the boundary of ψ=0, Equation (21.3) indicates the surface term 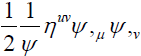 goes to infinite like the MIT bag model.
goes to infinite like the MIT bag model.
Back to the gravitational constant. If the field and matter are both trapped at the boundary, the total energy density of field and matter integrated over the space within the boundary shall give the total rest mass of the object. The solution of Equation (21.2) or Equation (19.2) will give the solution of ,ψ the Hamiltonian integration will define the constant G. If more mass is bombarded into the system, G will change, and the solution will also change with a different boundary.
Eq. (21.3) and Equation (19.2) are interesting because they recovered Newtons’ Law of gravity with an extra term of the self-interaction and the gravitation constant is the inverse of the field variable constant. The striking feature of Eq. (19.2) and Eq. (21.3) is that the gravitational constant enters the field equation naturally and defines the meaning of gravitational constant. Another feature of this Lagrangian is that if integration is done on both sides of Eq. (19.2), it gives the definition of matter and field energy momentum as the source of self-interacting field.
The Tensor version of Eq. (21.3) is
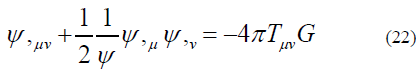
Unfortunately, Einstein’s General relativity is different from Eq. (22) because in the weak field limit, Einstein’s field equations recover Newton’s law of gravity not the Self-interacting Newton’s Law of Gravity which has second term of left-hand part of Eq. (22).
The equation (21.3) is very similar to the MIT bag model of strong interaction. The Lagrangian for scalar MIT bag model is as following:
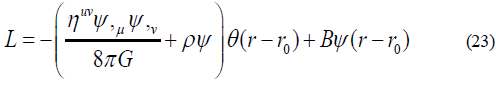
Where B is the surface energy.
The field equations for MIT bag model are
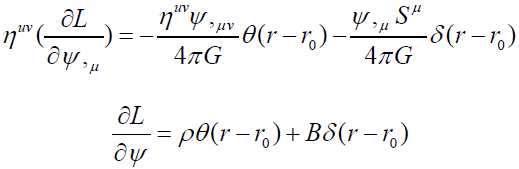
The equation within the surface
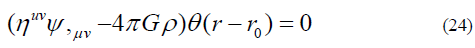
And the equation on the surface
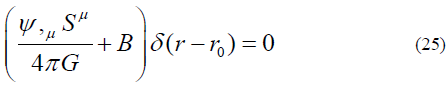
By definition, our self-interacting theory requires that there is a boundary when the field is strong enough. Equation (24) describes gravitational field within the boundary which is the equation of (21.3) except an extra term 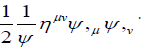 This extra term goes to infinite on the boundary when ψis zero. This extra term of (21.3) seems also to describe the surface field change dramatically.
This extra term goes to infinite on the boundary when ψis zero. This extra term of (21.3) seems also to describe the surface field change dramatically.
The property of self-interacting term: 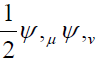
Let’s assume there are two masses and have two Newtonian fields:
ψ = ψ1 + ψ2 as a function of r and θexpansion of Eq. (19.3) as
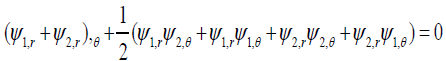
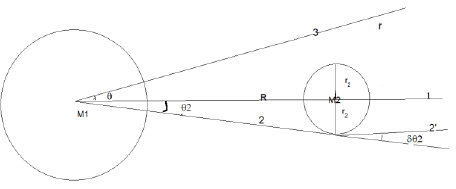
If the mass 1 is large and mass 2 is very small comparing with mass 1 as seen in figure 1.
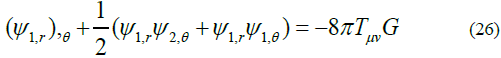
The field focusing by the Self-interaction in the solar system and in the galaxies has some effects are observable.
Comparing the terms of field strength changes in different directions:
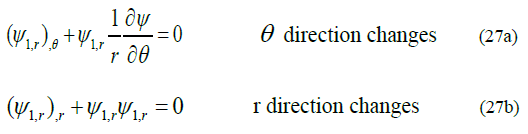
The force change due to θ direction change (a) 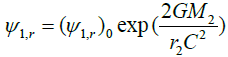 is where r2 is small, but
is where r2 is small, but 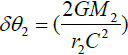 is reasonably small comparing with the original angle θ2.Note: r2 = θ2R. The force change due to direction change is amplified incomparison with the original angle where (ψ1,r)0 needs to meet the surface area change in Eq. (2). If the force is the surface density of field (field line is conserved), the true force due to the focusing is amplified by
is reasonably small comparing with the original angle θ2.Note: r2 = θ2R. The force change due to direction change is amplified incomparison with the original angle where (ψ1,r)0 needs to meet the surface area change in Eq. (2). If the force is the surface density of field (field line is conserved), the true force due to the focusing is amplified by 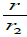 which is the inverse of the original angle. ψ1,r is the force from the M1.
which is the inverse of the original angle. ψ1,r is the force from the M1. 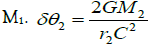 is the angle changed by M2 for the field line from M1.
is the angle changed by M2 for the field line from M1. 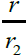 is the inverse of the original angle which is amplification factor. Theforce from the M1 will be focused by
is the inverse of the original angle which is amplification factor. Theforce from the M1 will be focused by 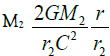 different from GR bending of light by a factor of 2 and an amplification factor. We do not have the full relativity field equations for this new self-Interaction theory yet. The total bending factor may be different from these calculations. But this does change the test of the assumptions of this theory. From Equation (27.a and 27.b) we see that Tμv will be re-focused and Equations (27) is non-Newtonian. The non-Newtonian part of Equation (27) can be observed when Saturn is behind the shadow of Jupiter. Near the surface of Mass M2, the ψ2,θ is not negligible in comparing with ψ1,r. If the matter energy momentum Tμv near the Mass M2 is zero,the second term of Eq. (27) is still important. It will cause the 1,rψchanges in theθdirection which is the focusing or de-focusing of fieldfrom mass M1. The direct extension of field focusing is that the field can also be trapped if the second terms of Eq. (27) is big enough. When ψ2,θ is small, the second term of Eq. (27) can be neglected. Equation(26) becomes Newtonian. The Extension of a non-Newtonian gravitation theory also requires the modification of Einstein’s field equations. The conservation of mesons (SI field) led to the strength change of the field. The focusing causes the ψ1,r change in direction(ψ1,r)θ, the change of direction can be small, but when the original open angel of the field is also small, the effects will be big. This term
different from GR bending of light by a factor of 2 and an amplification factor. We do not have the full relativity field equations for this new self-Interaction theory yet. The total bending factor may be different from these calculations. But this does change the test of the assumptions of this theory. From Equation (27.a and 27.b) we see that Tμv will be re-focused and Equations (27) is non-Newtonian. The non-Newtonian part of Equation (27) can be observed when Saturn is behind the shadow of Jupiter. Near the surface of Mass M2, the ψ2,θ is not negligible in comparing with ψ1,r. If the matter energy momentum Tμv near the Mass M2 is zero,the second term of Eq. (27) is still important. It will cause the 1,rψchanges in theθdirection which is the focusing or de-focusing of fieldfrom mass M1. The direct extension of field focusing is that the field can also be trapped if the second terms of Eq. (27) is big enough. When ψ2,θ is small, the second term of Eq. (27) can be neglected. Equation(26) becomes Newtonian. The Extension of a non-Newtonian gravitation theory also requires the modification of Einstein’s field equations. The conservation of mesons (SI field) led to the strength change of the field. The focusing causes the ψ1,r change in direction(ψ1,r)θ, the change of direction can be small, but when the original open angel of the field is also small, the effects will be big. This term 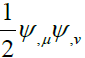 is from the self-interaction requirements which meet our assumptions to make the Newton’s gravity theory consistent with Einstein’s gravity theory in the classic physics domain. This is why we call the theory self-interaction field theory.
is from the self-interaction requirements which meet our assumptions to make the Newton’s gravity theory consistent with Einstein’s gravity theory in the classic physics domain. This is why we call the theory self-interaction field theory.
The classic version of SI field theory in 3-d, 2-d and 1-d trapping
The SI assumptions:
a). The Field or the mesons mediating the field follow the same geodesic equations in space time like the other particles.
b). Field strength is proportional to the number density of the mesons mediating field times the interaction time.
Assumption (a) leads to the conclusion that if the particles are trapped (like Einstein’s Black hole), the field will also be trapped. The particle will not interact with the surrounding matter like the strong interaction unless the spin of the particle is very strong and some of the particles (or virtual particles) will spin off the parent particles, like the quantum interactions.
Like the Blackhole of Einstein’s general relativity, for a 3-D spherical object,
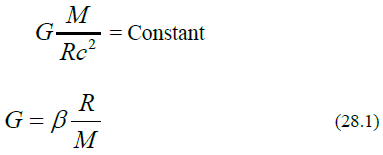
where 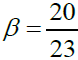 if the density is a constant and the field is spherically symmetric. Since the gravitational constant is proportional to the frequency of mesons mediating the gravitation (how many times the mesons bounce back and forth) which is inversely proportional to the field bound radius, that means
if the density is a constant and the field is spherically symmetric. Since the gravitational constant is proportional to the frequency of mesons mediating the gravitation (how many times the mesons bounce back and forth) which is inversely proportional to the field bound radius, that means

From Eq. (28.1) and Eq. (28.2),

The observable universe mass is 1080 of the nucleon mass, while the radius of the observable universe is 1040 times of the nuclei radius. This mass relationship between the universe and the nuclei is the square of the radius relationship between the universe and the nuclei which matches Eq. (28.3).
For the 2-dimension trapping, the field density in a 2-dimension space is inversely proportional to r (or 1/r force of the galaxy system). The potential for the 1/r force is ln 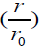 the integration of Eq. (20.2) for the 2-Dimension trapping gives the
the integration of Eq. (20.2) for the 2-Dimension trapping gives the
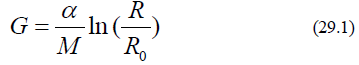
Using the Eq. (28.2), we see that based on Eq. (29.1), the mass relationship between 2-Dimention field bound object is proportional tothe radius. That is,

If the elliptical spiral galaxies are large enough and are fields 2-D trapped its mass shall be proportional to its 2-D radius.
For the 1-dimensional trapping, the field density in the 1-Dimentional trapped object is constant, that means the force is constant and the potential is proportional to r. The integration of Eq. (20.2) for the 1-D trapping give the

Using the Eq. (28.2), we see that based on Eq. (30.1), the mass relationship between 1- Dimensional field bound object is independent of the radius. That is,

It means the 1-Dimentional field bound string has the same mass for different scales.
Application of the scalar theory in astrophysics
One of the differences between this self-interaction field theory of gravitation and Newton’s law of gravity is that the gravitational field can be bent by the mass of an eccentric system, causing the focusing or de-focusing of the gravitational field. The effects of σs variation due to the focusing can be significant. An analysis of the field bending in galactic center, in the disk of the galaxies, the parallel field from the galactic center been focused by the Sun as well as the motion of Saturn under the influence of Jupiter is analyzed in the next four examples.
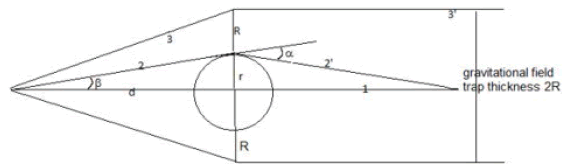
The gravitational field from mass M’ will be bent by mass M at distance d.The angle β expanded by the mass M at radius r by definition is

The deflection angle α of MMG by mass M to the first order of approximation is

If β is smaller than α, then geodesic 1 and geodesic 2 of MMG in figure 2 will intersect, σs is infinite, a in equation (5) goes to infinite at some point. There may be some interesting new physics near the area of infinite σs if the final field equations of gravitation which incorporates this self-interaction field theory.
Figure 2: The deflection of gravitational field from the source at distance d by mass M of radius r. if the deflection angle α is greater than expansion angle ( β ) of r over d, the gravitational field shall be intersect at somewhere on the axis defined by the source and mass M. if α = β, the gravitational field is parallel to the axis of the source and mass M and being trapped in 2D
If the expansion angle β is equal to deflection angleα, geodesic 1 andgeodesic 3 of MMG will be travelling parallel to each other after the deflection.
The analysis below is based on a first order approximation similar to the geometric optics with mass M as convex lens of MMG.
Example 1: The gravitation focusing by the galactic center
The distance D of infinite σs causing by the mass M (M’ is the sourceof MMG at distance d from M) is given by:
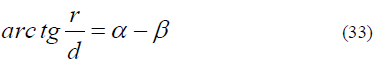
Thus,
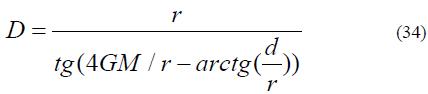
The galactic center Sagittarius A* may contain a “black hole” of M which is 4.1 million solar mass in a radius of r of 44 million km [2]. This gives the deflection angle of α.
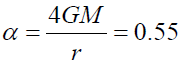
The deflection angle αby the mass at radius r seeing far away from thedeflection mass is about 31.50. There are many MMG geodesics that will intersect in space near the galactic disk and causing the local infinite gravitational force near Sagittarius A* according to Eq. (5).
A gravitational source of mass M’ at 4.4 billion kilometers (d equal to 100 times of radius r) away from Sagittarius A*, then the expansion angle is given by equation (31)
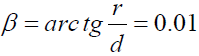
Putting the value of α and β into equation (33), it gives that D= 73.3million kilometers which means MMG from source M’ can be focused to infinite gravitation force by Sagittarius A* at 73.3 million kilometers (1.66 r) away from the center of Sagittarius A*. The gravitational force pattern defined by this self-interaction field theory will change dramatically due to MMG focusing by Sagittarius A*. There should be many new stars that are formed continuously due to the gravitational field focusing. The Youth Paradox [3], that the new stars forming near the galactic center may be the evidence of this theory which cannot be explained by Newton’s Law of gravity, based on which the tidal forces from the central Sagittarius A* to prevent their formation. The galactic nucleus is much more active than Newton’s Law of gravity can explain.
Example 2: Focusing by the disk of galaxies and the arm of the galaxies
A geodesic line of MMG travelling through the disk of a spiral galaxy will be bent many times by the mass it travels through. The total deflection can be projected towards the disk’s Z coordinate. It can be seen from the previous example, that the “black hole” will focus MMG to intersect. After leaving the center of the galaxy, the MMG will continue to be bent back to the disk because of the mass of the disk.
The total deflection angle
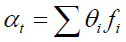
Where θi is the individual deflection angle and fi is the projection factor towards the disk axis Z. The total deflection angle needs to be calculated through a model of detailed statistics. A simple analysis will be presented here.
For a bending stars like the Sun in the disk, the deflection angle isαand its expansion angle to a source M’ is β If α=β, the MMG 3 in Figure 1 will be travelling parallel to MMG 1. Any source beyond 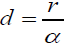 will be either parallel to 1 or intersect with 1. For the Sun, α is 0.848 ×10-5 and the radius of the Sun is 6.9 × 105 kilometer. Any source beyond d= 6.9 x 105 / 0.848 × 10-5 = 8.13 × 1010 = 1.16 × 10-2 light year will be bent to travel parallel to the axis of the source mass and the bending mass. For those MMG travelling parallel to the disk surface, the MMG is trapped in 2- dimension of the disk, σswill be inversely proportional to r, instead r2. By doing the same analysis, the gravitational field from one side is first bent by the mass on its way to the center, then bent by the center of galaxy, and finally by the mass on the other side of galaxy. Part of the gravitational field is going to be parallel to the galactic disk due to the focusing by the center and the mass in the disk. All field lines parallel to the disk will be trapped in a 2-dimension surface. In two dimension (3 dimension if plus time),
will be either parallel to 1 or intersect with 1. For the Sun, α is 0.848 ×10-5 and the radius of the Sun is 6.9 × 105 kilometer. Any source beyond d= 6.9 x 105 / 0.848 × 10-5 = 8.13 × 1010 = 1.16 × 10-2 light year will be bent to travel parallel to the axis of the source mass and the bending mass. For those MMG travelling parallel to the disk surface, the MMG is trapped in 2- dimension of the disk, σswill be inversely proportional to r, instead r2. By doing the same analysis, the gravitational field from one side is first bent by the mass on its way to the center, then bent by the center of galaxy, and finally by the mass on the other side of galaxy. Part of the gravitational field is going to be parallel to the galactic disk due to the focusing by the center and the mass in the disk. All field lines parallel to the disk will be trapped in a 2-dimension surface. In two dimension (3 dimension if plus time),
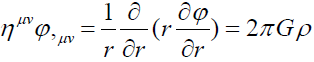
Assume: 1). Disk matter density ρ is zero (small) like the galaxy disk, but the disk has enough matter to bend the field up and down of the disk. 2). ϕ is only a function of radius of the disk r.
Then,

Thus, the stars far away from the galactic center are affected by the force generated by the field trapped in the galactic disk gives a constant rotational curve 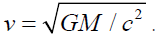 The rotation curve of the globular clusters (no disk, no eccentric mass distribution) will not have this kind of property. In the bar of the galactic center, the MMG will be trapped in the bar (1 dimension) and gravitational force shall be constant. This is maybe the reasoning of the star formation in the Milky Way arms. In the arm of the galaxy, the field is trapped in 1 dimension, the force is a constant, The above rotation curve equation become
The rotation curve of the globular clusters (no disk, no eccentric mass distribution) will not have this kind of property. In the bar of the galactic center, the MMG will be trapped in the bar (1 dimension) and gravitational force shall be constant. This is maybe the reasoning of the star formation in the Milky Way arms. In the arm of the galaxy, the field is trapped in 1 dimension, the force is a constant, The above rotation curve equation become
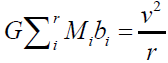
which gives a rotational curve 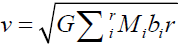 increases as square root of r, where bi is the force contribution by the ith mass. Both the constant rotational curve and rotation curve which increases as a function of square root of r have been observed [4].
increases as square root of r, where bi is the force contribution by the ith mass. Both the constant rotational curve and rotation curve which increases as a function of square root of r have been observed [4].
Example 3: The kuiper belt and binary stars
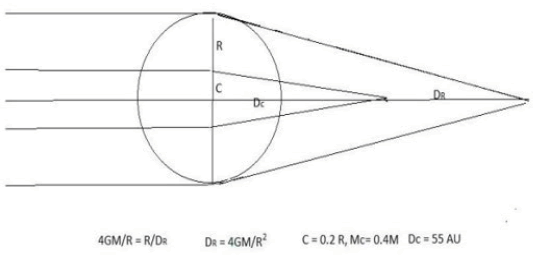
In the above two analyses, the Youth Paradox and the flatting of rotation curve cannot be tested easily to confirm the Assumption of this paper. Applying this theory to the solar system can be very interesting. Assuming the focusing like the General relativity, if the parallel field from far away stars or the Galactic center like in the figure 3, the focus point of the gravitational field by the Sun will be at point D where:
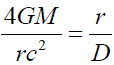
Thus, 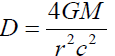
If the core of the sun has 40% of solar mass within 0.2 radius. Then Dc = 0.813 × 1010 km = 55 AU. If 50% of the mass is within the 0.2 radius, Dc = 0.65 × 1010 km = 43 AU. The Kuiper belt is a reasonable guess of this focusing where the data is from Reference [5]. The Kuiper belt later on as it is accumulating mass, may form another star. This is also maybe the reason for the abnormal percentage of stars are binary stars. If this explanation of Kuiper belt is correct, there would be more binary stars for massive stars compared with the lower mass stars which is in fact observed [6]. For a massive star, the Kuiper belt is closer to the primary star, the gravitational field from the primary star is able to bind the companion star together.
The Kuiper belt can be used to test the assumptions of this theory. From Part II of this serial of papers and the conclusion of section 3 of this paper, it is clear that the strong interaction and gravitation are in the same equation. The focusing of gravitation can cause the formation of strong interaction or hydrogen particles. If the telescopes of monitoring the formation of hydrogen in the Kuiper belt gives the asymmetry intensity comparing the galactic center direction with the opposite direction, it will indicate the Sun is focusing the gravitation to a point and forming the hydrogen. Current Newton’s Law of gravity and Einstein’s GR will not lead to this kind of conclusion.
Example 4: The ring of saturn and maybe abnormal behavior in the shadow of jupiter
In the case of solar system, the Sun is the source of gravitation, while take the Jupiter as the bending mass, where d>>r the solar gravitational field deflected by the Jupiter. The force of the Sun after Jupiter and far away from Jupiter, is amplified by a factor in the σs as Saturn travelling in the φ coordinate and located a Z distance above the rotational surface (Figure 4).
The original expansion angle βs of Saturn is
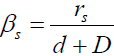
Where rs is the radius of Saturn d is the Jupiter distance to the Sun and D is the distance between Jupiter and Saturn. The angle βs times d is the impact parameter difference, thus the two MMG has different bending angle and the amplification factor A of the angle comparing with the original expansion angle in the Z direction is:
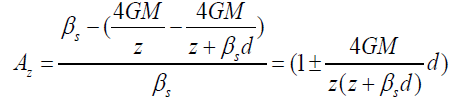
Where ‘+’ is for Saturn is below the rim of the Jupiter shadow and “-“ is for Saturn is above the rim of the shadow. If Saturn’s center is right at the rim, then the total amplification factor is zero, but Saturn will experience the tidal force (upper half has less solar force and lower half has stronger solar force. If Z is smaller than the radius of Jupiter, M = 4πρ(Z)3/3 and the amplification factor Az takes the positive sign.

The amplification factor in the θ direction is given by:
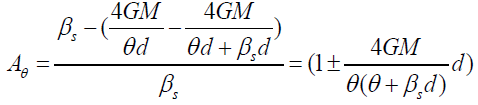
Where ‘+’ is for Saturn is away the rim of the Jupiter shadow and “-“ is for Saturn is inside the rim of the shadow. If Saturn’s center is right at the rim, then the total amplification factor is zero, but Saturn will experience the tidal force (outside half has less solar force and inside half has stronger solar force). If θd is smaller than the radius of Jupiter, M = 4πρ(θd)3/3 and the amplification factorAθ takes the positive sign.
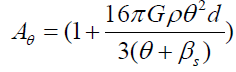
Based on Equation (5), to the first order of approximation, the acceleration of Saturn has the following form passing the shadow of Jupiter at Z:
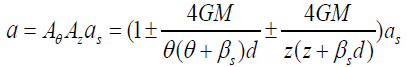
Whereas as is the acceleration without the gravitational field deflection. The amplification factor  when Z the radius of Jupiter, Az is 1.113 x 104. a = (1.0 - 0.95 x 103) as is about 0.95 x 10-3 smaller thannormal if Saturn is just off the rim of the Jupiter shadow (Figure 4) or about 0.95 x 10-3 bigger if Saturn is just inside the shadow of Jupiter.This result shall be observable to confirm the Assumption of this paper. This disturbance of the path by Jupiter may be the reason for the large number of smaller objects near Saturn. The field abnormal strength changes when Saturn is in the shadow of Jupiter, over many years, it may cause the force stronger than the tidal force and causing the ring of the Saturn.
when Z the radius of Jupiter, Az is 1.113 x 104. a = (1.0 - 0.95 x 103) as is about 0.95 x 10-3 smaller thannormal if Saturn is just off the rim of the Jupiter shadow (Figure 4) or about 0.95 x 10-3 bigger if Saturn is just inside the shadow of Jupiter.This result shall be observable to confirm the Assumption of this paper. This disturbance of the path by Jupiter may be the reason for the large number of smaller objects near Saturn. The field abnormal strength changes when Saturn is in the shadow of Jupiter, over many years, it may cause the force stronger than the tidal force and causing the ring of the Saturn.
From the following table of planets in our solar system, there may be a missing star between Jupiter and Mars. The focusing that happened before Jupiter can cause dynamic changes right before the gravitational field from the Sun reaches Jupiter. The missing star between Mars and Jupiter shall be in the line of Jupiter and the Sun compared with the star beyond Jupiter (Saturn). The other effects of this focusing may happen beyond Jupiter. The ring of Saturn may be caused by Jupiter gravitational focusing. These two effects can be tested near Jupiter within the Sun shadow of Jupiter (Table 1).
TABLE 1 The distance between Mars and Jupiter has a big jump and Saturn has a unique ring
| Name | Distance from the sun | Revolution period | Diameter | Mass | Density | |
|---|---|---|---|---|---|---|
| [AU] | [y] | [km] | [1023km] | [g/cm3] | ||
| Mercury | 0.39 | 0.24 | 4878 | 3.3 | 5.4 | |
Venus |
0.72 | 0.62 | 12120 | 48.7 | 5.2 | |
Earth |
1 | 1 | 12756 | 59.8 | 5.5 | |
Mars |
1.52 | 1.88 | 6787 | 6.4 | 3.9 | |
Jupiter |
5.2 | 11.86 | 142948 | 18991 | 1.3 | |
Saturn |
9.54 | 29.46 | 120536 | 5686 | 0.7 | |
Uranus |
19.18 | 84.07 | 51118 | 866 | 1.3 | |
| Neptune | 30.06 | 164.82 | 49660 | 1030 | 1.6 |
Discussions on the interactions different field-bound object and quantum entanglement
Einstein’s general theory of relativity introduces self-interacting terms to the field equations which is not in the classical Newton’s law of gravity. In the weak field limit, the self-interaction terms are small even in general relativity. It is clear from section 4, scaler version of self-interacting field is different from the classical Newton’s Law of gravity with extra terms. These extra terms cannot be negligible for asymmetrical systems. It will cause the focusing and defocusing of the field. The strength change is not because of the field variable, but the conservation of the number density which increases the strength of the field when the field is been focused.
Non-linearity allows more solutions than Newton’s Law of gravity. This is unique for unification of Microscale to Macroscale. The 3-D confinement allows the field and the object to form a membrane surface of very strong interaction on the surface and non-interaction outside of the surface. The 2-D and 1-D confinement of the SI field allow the bound object to interact with each other through a surface or a line.
Even though the SI field theory was proposed for gravitation. The field-being-trapped is the key assumption of the SI field theory. The SI field theory recovers the Dirac Large number principles from the two assumptions. It seems that the theory also includes the strong self-interaction which may be the strong interaction in the nuclei or other interaction which binds the other elemental particles together. It will show in Part II of this series of paper that quantum mechanics can be described using this SI field theory. How physics equations behave within the boundary of elemental particles is unclear, but the behaviors for our universe can be described and tested.
The quantum entanglement state can be easily explained based on this self-interaction field theory: When a particle or photon A is leaving a source, A may exchange the 1-D confinement field or mesons between Aand another particle B in source. They form a SI field boundary within which the physics is unknow to us or the observer. A and B can interfere with each other like a wave. If the observer observes particle A, the observation has to break the 1-D confinement field, A and B will notinterfere with each other anymore. The quantum entanglement is due to the 1D Self-interaction field exchange forming a boundary and make them in a “universe” which may have different physics constant.
The scalar version of the self-interacting field is very interesting in macroscale. It can be tested when Saturn is within the shadow of Jupiter (even before the shadow of Jupiter) due to the solar field being focused or de-focused. Testing of SI field theory is crucial for the future of this theory.
References
- Dirac PAM. Cosmological Models and the Large NumbersHypothesis. Proc R Soc Lond. 1974: 338 (1615); 439â??46
- S Gillessen. Monitoring stellar orbits around the Massive Black Hole in the Galactic Center Astrophys, J. 2009: 692 (2); 1075â??1109
- Robert H. Sanders, Revealing the Heart of the Galaxy: The Milky Way and its Black Hole. Camb. Univ. Press. (2013). Online ISBN: 9781139856546
- Rubin, V.C.; Thonnard, N.; Ford, W.K. Jr. (1978). "Extended rotation curves of highluminosity spiral galaxies.IV â?? Systematic dynamical properties, SA through SC". The Astrophysical Journal Letters. 225: L107â??L111.
- Stern, Alan; Colwell, Joshua E. "Collisional erosion in the primordial Edgeworth-Kuiper belt and the generation of the 30â??50 AU Kuiper gap". The Astrophysical Journal. 490 (2) (1997). 879â??882.
- Duchêne, Gaspard; Kraus, Adam "Stellar Multiplicity", Annual Review of Astronomy and Astrophysics, 51 (1) (2013): 269â??31.