The symmetry of N-domain and prime conjectures

Received: 27-Dec-2022, Manuscript No. puljpam-22-6002; Editor assigned: 29-Dec-2022, Pre QC No. puljpam-22-6002 (PQ); Accepted Date: Jan 03, 2023; Reviewed: 31-Dec-2022 QC No. puljpam-22-6002 (Q); Revised: 02-Jan-2023, Manuscript No. puljpam-22-6002 (R); Published: 30-Jan-2023, DOI: 10.37532/2752-8081.23.7(1).20-21.

Citation: Yajun L. The symmetry of N-domain and prime conjectures. J Pure Appl Math. 2023; 7(1):20-21.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

In this paper, we discuss the symmetry of N-domain and we find that using the symmetry characters of Natural Numbers we can give proofs of the Prime Conjectures: a concise proof of Fermat last theorem Polignac’s conjecture (twins Prime Conjecture) Goldbach Conjecture and Reimann Hypothesis. 

Keywords

N domain; Prime conjectures

Introduction

We have

N ~（ 0,1,2,3,4,...........） all the natural numbers

n ~（ 1,2,3,4,...........） all the natural numbers excepted 0

P ~（ 2,3,5,7,...........） all the prime numbers

p ~（ 3,5,7,...........） all the odd prime numbers

We notice that

N ~（ 0, n）

P ~（ 2, p)

1: The proof of twin primes conjecture and goldbach conjecture

Figure 1: The Symmetry of N-domain

Figure 2: All the non-trivial Zero points of Riemann zeta-function are on the 1/2 axis

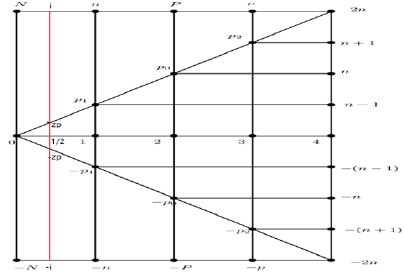
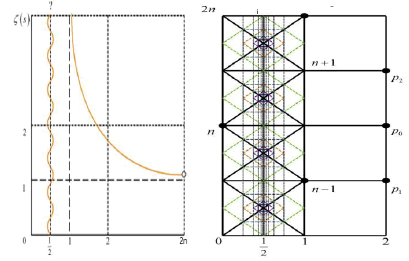
We can define a N, n, P, p, 2n coordinate system shown in Figures 1 and 2.

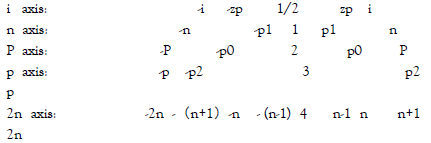
p1, p0, p2 ∈ p

we can get

p1 → n - 1

p0 → n

p2 → n + 1

And

- p1 → - (n-1)

- p0 → -n

- p2 → - (n+1)

So we have

p2 + (- p1) → n + 1 - (-(n-1)) = 2n

This is the proof of Polignac’s conjecture.

And

p2 - p1 → (n+1) - (n-1) = 2

This is the proof of twin primes conjecture.

And

2n = n + 1 + n - 1 → p2 + p1

And

n -1 > 2 n > 3 so 2n > 6

This mean that every even number bigger than six can be divided into two odd prime numbers in N domain.

This is the proof of Goldbach conjecture.

2: The proof of Riemann Hypothesis

Riemann Zeta-Function is

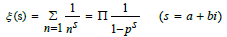
Riemann hypothesis

All the Non-trivial zero-point of Zeta-Function Re(s ) = 1/2 .

We have

0 = 1 / 2 - 1 / 2

1 = 1 / 2 + 1 / 2

i2 = - 1

1 / 2 = 1 / 2 * (1/2+1/2i) (1/2-1/2i)

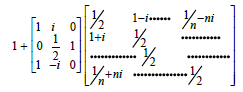
The tr(A)=1/2*n

This is mean that all the non-trivial Zero points of Riemann zetafunction are on the 1/2 axis just show as Fig.3. This is the proof of Hilbert–Pólya conjecture. So we give a proof of Riemann Hypothesis (Figures 2 and 3).

Figure 3: The p/2n function

3: A concise proof of fermat’ last theorem

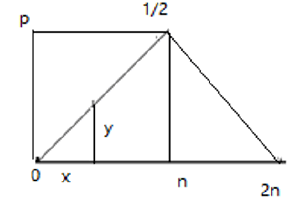
We can definite a function as

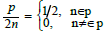
So x + y = n

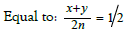
And x + y ∈ p

x² + y² = n²

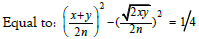
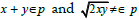
But we notice that:

When x + y = 3∈p xy = 3 (x = 1, y + 3)

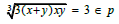
This is equal to X³ + Y³ = n³ has no integer solution. This is a concise proof of Fermat’ last Theorem.