The way to list all infinite real numbers and to construct a bijection between natural numbers and real numbers

Received: 29-Apr-2022, Manuscript No. puljpam-22-4879; Editor assigned: 09-May-2022, Pre QC No. puljpam-22-4879(PQ); Accepted Date: Jul 04, 2022; Reviewed: 06-Jun-2022 QC No. puljpam-22-4879(Q); Revised: 20-Jun-2022, Manuscript No. puljpam-22-4879(R); Published: 06-Jul-2022, DOI: 10.37532/2752-8081.22.6.4.6-8.

Citation: Chen SP. The way to list all infinite real numbers and to construct a bijection between natural numbers and real numbers. J Pure Appl Math 2022;6(4):6-8.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

Georg Cantor defined countable and uncountable sets for infinite sets. The set of natural numbers is defined as a countable set, and the set of real numbers is proved to be uncountable by Cantor’s diagonal argument. Most scholars accept that it is impossible to construct a bijection between the set of natural numbers and the set of real numbers. However, the way to construct a bijection between the set of natural numbers and the set of real numbers is proposed in this paper. The set of real numbers can be proved to be countable by Cantor’s definition. Cantor’s diagonal argument is challenged because it also can prove the set of natural numbers to be uncountable. The process of argumentation provides us new perspectives to consider about the size of infinite sets.

Key Words

Cantor’s diagonal argument; countable set; uncountable set; set theory

Introduction

Infinite is an unclear concept, and many scholars try to describe or define it. Most mathematicians believe that “infinite for natural numbers” and “infinite for real numbers” are different. Mathematicians can easily list all infinite natural numbers by order: 1-5. However, people cannot give any rule to list all infinite real numbers by order. In set theory, the sets with infinite members are concerned and debated. Georg Cantor defined countable and uncountable sets for infinite sets. For example, the set of natural numbers (N) is countable, and the set of real numbers (R) is uncountable. The main concepts of Cantor’s definition for countable sets are:

Concept 1: If all of the infinite members in a set can be listed by any rule, then the infinite set is countable. Otherwise, the infinite set is uncountable.

Concept 2: According to the definition given above, N is a countable set.

Concept 3: For any infinite set X, X is countable if and only if there is a bijection between X and N.

The concepts are approved and applied by most scholars up to now. Under the concepts and definition, Georg Cantor believed and suggested that it is impossible to construct a bijection between N and R. Furthermore, R is proved to be uncountable by Cantor’s diagonal argument [1, 2]. The proof can be briefly described as follows:

StepA1: Assuming that R is countable.

StepA2: Under the assumption, the members in R can be listed by order. Any part of the members in R can be listed by order. Real numbers between 0 and 1 can be listed by order.

StepA3: Each real number can be represented by infinite decimal. For example:

0.1 = 0.100000000……

0.25 = 0.250000000……

0.597 = 0.597000000……

StepA4: Each real number between 0 and 1 can be represented by infinite decimal and can be listed. Mark them as s1, s2, s3,… , sn, ……

s1 = 0.100000000……

s2 = 0.333333333……

s3 = 0.597570255……

s4 = 0.627898900……

s5 = 0.255555555……

s6 = 0.777777777……

s7 = 0.101010101……

s8 = 0.976662555……

s9 = 0.010101010……

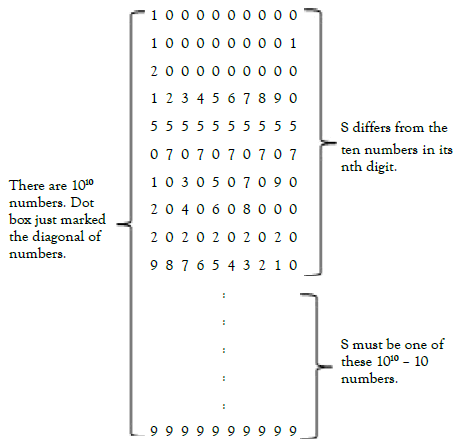
StepA5: When all real numbers between 0 and 1 are listed. We can construct a number S and let S differs from sn in its nth digit (Notice bold digits marked in StepA4):

1st digit of S cannot be 1

2nd digit of S cannot be 3

3rd digit of S cannot be 7

4th digit of S cannot be 8

5th digit of S cannot be 5

StepA6: S is a real number. S is not any one real number listed above, since their nth digits differ.

StepA7: All real numbers between 0 and 1 are listed, so S should be listed (Step A5). However, S is not any one real number in the list (Step A6). There is a contradiction under the assumption at Step A1.

StepA8: The assumption at Step A1 is wrong, so R is uncountable. However, N will be proved to be uncountable using Cantor’s diagonal argument, and R will be proved to be countable by Cantor’s definition in this paper. The results of argumentation will subversively change the concept of “infinite” in set theory, and the process of argumentation will provide us new perspectives to consider about the size of infinite sets.

Argument 1: The set of natural numbers could be uncountableN can be proved to be uncountable by Cantor’s diagonal argument:

StepB1: We know that nature number could be represented as different formats:

1 = 01 = 001 = 0001 = ……01

2 = 02 = 002 = 0002 = ……02

3 = 03 = 002 = 0003 = ……03

StepB2: As StepA4 of Cantor’s diagonal argument, all natural numbers can be listed:

N1 = …………000001

N2 = …………000002

N3 = …………000003

N12345 = …………012345

StepB3: Note that the numbers listed at StepB2 are all natural numbers. It means that all numbers listed at StepB2 are finite non-zero digits.

A natural number S can be constructed as:

S differs from Nn in its nth digit in these finite non-zero digits. It makes S be finite non-zero digits, too. Thus, S can represent a natural number.

StepB4: By the construction, S differs from each Nn, since their nth digits differ. According to the logic of Cantor’s diagonal argument, the N has been proved to be uncountable. I suggest that Cantor’s diagonal argument cannot prove an infinite set is countable or not. The key point is that infinite numbers cannot be listed of all (StepA4 or StepB2 cannot be completed).

Argument 2: The set of real numbers is countable

Most scholars accept that it is impossible to construct a bijection between N and R. Also, people cannot give any rule to list all of the infinite R members.

However, I give a rule to list all of the positive R members:

To simplify the description, the above rule just lists all of the positive R members. It is easy to expand the rule to lists all of the R members and unnecessary to go into details here. Based on the above rule, we can construct a bijection between N and R by following steps:

Rewrite all natural numbers as the same method described at

StepC4: Rewrite all real numbers as the sequence:

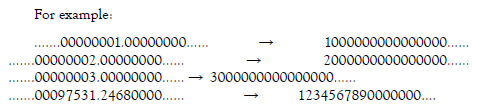
Then, we get a bijection between positive real numbers and natural numbers. Consider of positive number, negative number and zero, we get a bijection between the set integer numbers (Z) and R.

StepC5: According to the countable set theory, there is a bijection between N and Z. So there is a bijection between N and R. According to aforesaid Concept 3, R is countable.

Moreover, it is easy to see that there is a bijection between N and the set of complex numbers (C) by similar demonstration process. Each complex number could be written as X + Yi, and both x and y are real numbers. We could rewrite complex number by following rules:

Then, we can finally get a bijection between N and C.

Discussion

There is a new perspective of the contradiction in the Cantor’s diagonal argument. If we examine the Cantor’s diagonal argument carefully, we can find it is not “diagonal” exactly. We simply consider the arrangements of 2 numbers.

There will be 4 arrangements:

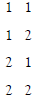
Cantor’s diagonal argument regards it as 2 arrangements, so it looks like “diagonal”.

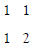
We can construct S (as StepA6) and let its 1st digit is not 1 and its 2nd digit is not 2. S is not any one listed above, since their nth digits differ. However, S will be one of the full 4 arrangements:

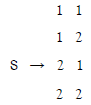
If we can list all real numbers (such as the rule given above), then we cannot construct S and let S differs from sn in its nth digit . For example:

The contradictions at StepA7 makes Georg Cantor reject the assumption at StepA1, but it actually makes us reject the The construction of S is after that all infinite numbers are listed. There should be a rational feature of infinite numbers: infinite numbers cannot be listed of all, or they are not infinite. In my opinion, the number S constructed at StepA5 proves that StepA4 is impossible to complete, but not proves that the assumption at StepA1 is wrong.

I propose that we always can find appropriate rewrite rules to get a bijection between any two infinite sets under current concepts of set theory. In these demonstration processes, we find that it is not necessary to define countable or uncountable for infinite sets. It is nonsense to compare sizes of infinite sets because their members are all infinite. The term, size, is defined to describe finite numbers. Related question developed from the concepts of countable or uncountable, such as continuum hypothesis, will be solved by the new concept without countable or uncountable.

References

1. Cantor G. On a property of the collection of all real algebraic numbers. J Reine Angew Math. 1874;77:258–62.
2. Kanamori A. Set theory from Cantor to Cohen. In Handb Philos Sci Philos Math, Andrew D Irvine; N.-Holl. 2009; 395–459.