Thermal and particle diffusion waves describe the relative mass of free standard model particles
2 Advanced Physics Initiatives, 57-58 Russell Square, London, WC1B 4HS, UK, Email: jhowardo.slater@uclmail.net
Received: 22-Feb-2023, Manuscript No. puljpam-23-6184; Editor assigned: 24-Feb-2023, Pre QC No. puljpam-23-6184 (PQ); Accepted Date: Mar 28, 2023; Reviewed: 28-Feb-2023 QC No. puljpam-23-6184 (Q); Revised: 06-Mar-2023, Manuscript No. puljpam-23-6184 (R); Published: 31-Mar-2023, DOI: 10.37532/2752-8081.23.7(2).53-63
Citation: Mandelis A, Slater JHO. Thermal and particle diffusion waves describe the relative mass of free standard model particles. J Pure Appl Math. 2023; 7(2):53-63.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
Thermal Diffusion Wave (Thermon) and Particle Diffusion Wave (PDW) dynamics are derived from an ensemble of Pre-Particles (PP) acting as heat engines. Once a steady state, non-linear logistic equilibrium of Thermon and PDW is established, the particles are stabilised and SM particles form by interacting with harmonic distributions of Thermon and PDW dynamics. The experimental observations confirm that this mechanism generates SM particle masses, and presumably conform with Quantum Field Theory (QFT). Expectations relationship between Thermon-PDW dynamics and QFT is not known. The new Thermon-PDW hypothesis has a key feature, the continuous flux of thermal energy to drive the Thermon and PDW. Concomitantly, sub-models describes the appearance of dynamics resembling gravitational and universe time properties.
Keywords
Thermal Diffusion Wave; Thermon; Particle Diffusion Wave; PreParticle (PP); Pre-universe; Steady State Non-equilibrium; Standard Model (SM) of Particles; SM Particle Mass; Standard Rank Number; Modified Rank Number; Thermophoresis; Universe; Gravity, Universe Time (UT)
Introduction
The fermion and boson mass measurements are accurately known, but it is not known why “free” (or isolated or bare) Standard Model (SM) particles have the observed mass values. For example, Blumhofer and Hutter modelled fermion mass relationships, concluding that “fermion mass models … fail to predict the exponential mass spectrum of the Standard Model in a natural way [1-3]. Griffiths commented: “Why do the bare quarks have the particular masses they do? Is there some pattern here? The Standard Model offers no answer, it is the business of theories beyond the Standard Model to say where they come from” [4]. Preliminary observations suggested that in an “ensemble” (or community, group or assemblage) in a common local environment of free SM particles there are interactions between the constituent free particles [5]. The terminology used in our publications needs to be crystal clear as follows: the mathematical analysis reported in this paper refers to Pre-Particles (PP) which are not free SM particles or SM bound. It is assumed that free SM particles exist initially without reference to the principles and mechanisms of Quantum Field Theory (QFT), recognising that SM particles masses will change when combined or grouped. We must be clear that an ensemble is not the product of QFT, it is the precursor. The importance of interactions between particles in an ensemble are analogous to organism population and community ecology dynamics, especially the kinetics of stability, response to environmental perturbation and harmonic relationships [6-9]. These mathematical models are normally based on the non-linear logistic function, widely used in many venues, particularly when the dynamics involve stable oscillations, gradients or harmonic patterns, under steady state non-linear equilibrium conditions [10, 11]. The difference equation described by May, originally derived by Verhulst, is:

where: H=population parameter (biomass); r=rate constant The May/Verhulst difference equation generates wave-like dynamics, responding to continuous thermal flow. Incorporating these spatiallydamped thermal oscillation dynamics, comparable to Schrodinger’s linear partial differential equation, into Angstrom diffusion wave dynamics Grossing introduced the concept of “quantum potential” within a thermodynamic framework [12-15]. This showed that the classical diffusion equation (Fick’s second law) leads to the Schrödinger equation without resorting to quantum mechanical formalisms. Schrödinger observed that the “correlation of all features of physical phenomena can probably be afforded only by a harmonic union of these two extremes” [namely, either] “mass-points of definite mass and charge” or “the theory of atomic [i.e. quantum] mechanics” [12]. The balanced combination of a quantum thermal diffusion framework with classical particle diffusion due to momentum fluctuations leads to the “Thermon PDW Hypothesis” to give SM particles’ relative mass values [16].
Free SM particles relationship is a harmonic sequence
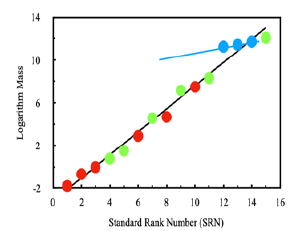
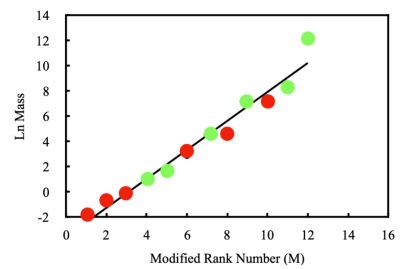
Experimental observations and methods for their experimental confirmation assume that the free SM particle masses are the same as for the equivalent pre-particles (PPS). Free SM particle mass sizes show no patterns within or between various free SM particle groups [2]. However, if the 15 free SM particles with mass (excluding photon and gluon) are treated as a single group ranked by increasing mass, then there is a linear relationship between the Standard Rank Number (SRN) and the ln of free particle mass (Figure 1). Separating the particles into three categories: 3 free bosons, 6 free leptons and 6 free quarks, a Modified Rank Number (MRN) is assigned (Table 1).
TABLE 1 Tabulation of the relationship values between the logarithm of elementry particle mass (MeV/c-2) and the standard rank number (S) or modified rank number (M) where the modified rank is given by 1 …+ (n+1) with the coefficient of correlation (R2) for each group n/s- data not shown in associated figure.
| Elementry of particle group | Fig | Rank Number (Standard or Modified) | Gradient |
Intercept |
R2 | |
|---|---|---|---|---|---|---|
| 15 Leptons, quarks & bosons elementry particles (S) | 1 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 | S | 1.08 | -3.21 | 0.98 |
| 12 Laptons & quarks (S) | 5 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 15 | S | 1.02 | -2.99 | 0.99 |
| 12 Leptons & quarks (M) | n/s | 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 | M | 1.15 | -3.54 | 0.97 |
| 6 quarks (S) | 3 | 4, 5, 7 , 9, 11, 15 | S | 1.04 | -3.12 | 0.98 |
| 6 quarks (M) | n/s | 1, 2, 3, 4, 5, 6 | M | 2.26 | -2.19 | 0.97 |
| 6 Leptons (S) | 4 | 1, 2, 3, 6, 8, 10 | S | 0.99 | -2.85 | 0.99 |
| 6 Leptons (M) | n/s | 1, 2, 3, 4, 5, 6 | M | 1.86 | -4.42 | 0.96 |
| 3 bosons (S) | 2 | 12, 13, 14 | S | 0.22 | 8.62 | 0.98 |
| 3 bosons (M) | n/s | 1, 2, 3 | M | 0.22 | 11.04 | 0.94 |
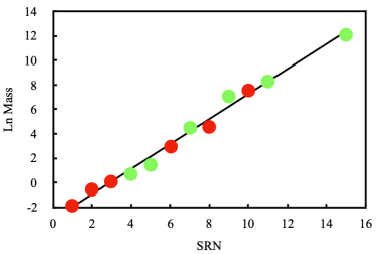
Comparing rank number against particle mass indicates that the 3 free boson group (SRN 12, 13 & 14 or MRN 1, 2 & 3; Table 1) is not related in exactly the same way since the SRN gradient is about 20% of the single 12 free fermion group gradient (Figure 1 and Table 1). The 3 free bosons have a similar pattern, nevertheless, suggesting a common property between boson and fermion categories. Relative mass orders between groups are not always maintained, for example, neutrinos and bosons show an inversion in the MRN sequence (Table 2). But for leptons and quarks as separate categories there is striking similarity, suggesting that the exact rank position in the group is significant (Figure 2 and Table 1). This is endorsed by the MRN leptons and quarks since their positions are defined without reference to individual particles in the other groups (Figure 3 and Table 1).
TABLE 2 Variations in Standard Rank Number (SRN) and Modified Rank Number (MRN) with respect to order and position differences for SM paticles with mass
| Group | SM Generation Number* | Order Comparision | Position Difference | |||
|---|---|---|---|---|---|---|
| I | II | III | I/II | II/ III | ||
| Quarks | Up | Charm | Top | |||
| SRN | 4 | 9 | 15 | Same | 5 | 6 |
| MRN | 1 | 4 | 6 | Same | 3 | 2 |
| Quarks | Down | Strange | Bottom | |||
| SRN | 5 | 7 | 11 | Same | 2 | 4 |
| MRN | 2 | 3 | 5 | Same | 1 | 2 |
| Leptons | Electron | Muon | Tau | |||
| SRN | 2 | 8 | 10 | Same | 6 | 2 |
| MRN | 1 | 5 | 6 | Same | 4 | 1 |
| Leptons | E-Neutrino | M-Neutrino | T-Neutrino | |||
| SRN | 3 | 1 | 6 | Invert I & II | -2 | 5 |
| MRN | 3 | 1 | 4 | Invert I & II | -2 | 3 |
| Bosons | Z-boson | W-boson | Higgs-boson | |||
| SRN | 13 | 12 | 14 | Invert I & II | -1 | 2 |
This predicates a thermal flow mechanism involving mutual interactions between individual free leptons and free quarks, which is crucial to understanding why the masses are as they are. So, an interaction mechanism due to thermal flow in free particles fundamentally effects quantum mechanics. The 12 free particle group is a harmonic relationship, requiring a precise mechanism to explain the observed masses.
Thermal and particle diffusion waves hypothesis
Basic Model: Non-linear logistic thermal and particle diffusion wave equation
In the following sections: “particle” means “pre-particle”, and relative (normalised) masses are considered rather than absolute values. In an ensemble of pre-particles (PPs) in a 1D-space, the diffusion wave equation is derived from the logistic difference equation Eq (1) [8,9] as:

where replacing Hn in Eq (1), Nt = particle density at time t; a and b=constant coefficients. Using a Taylor expansion:
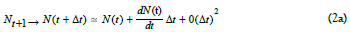
and, allowing for a spatial coordinate dependence of particle density, Eq (2) becomes a partial differential equation:
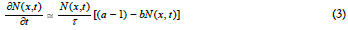
where, in the limit Δt → 0, Δt=τ which is a characteristic time for the particle ensemble system defined in diffusive motion terms.
Eq (3) is solved with a ≠ 1 and b ≠ 0 to yield:
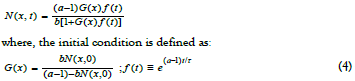
where, the initial condition is defined as:
The particle density distribution is an exponential increase for a>1 or a decay for a<1. These trends are consistent with May’s mathematical analysis of population growth leading to divergence or decay [8, 9].
If b=0, Eq (4) becomes:

If a=1, the Eq (3) solution is a decaying time profile:
The spatial distributions of particles in unidimensional motion in density gradients are due to temperature gradients arising from the motion of particles as dissipative systems [14]. For a 1D-ensemble of particles, characterised by size and energy and each separated by a mean distance from its nearest neighbor, the rate equation for the particle population, Ni(x, t), (particles.cm-3) is given by the net rate of particles hopping into, and out of, the location, i:
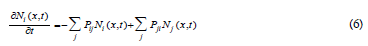
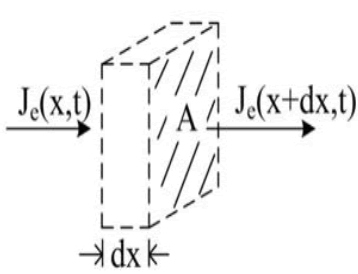
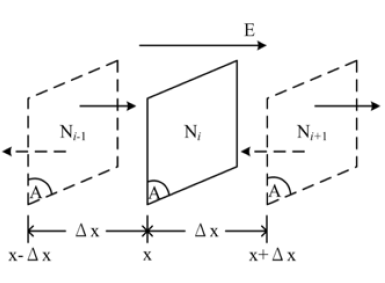
where Pij=probability of a particle migrating from location i to j. For a 1D-flow of particles passing through a virtual volume element, dV=Adx (Figure 4), the net
particle flux, Je (x,t) , [particles.cm-2.s-1] across cross-sectional area, A, is:
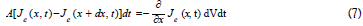
The net rate of particles entering space, dV, in time, dt, is found from Eqs (6) & (7):

where the right-hand side represents particles entering and/or leaving the volume without any local loss (sink) or generation (source).
So from Eqs (6) & (8):
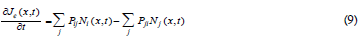
Nearest Neighbour (NN) approximation simplifies the Eq (9) summation, to show particle flux kinetics in a 1D-space (Figure 5). In a particle gradient, the net flux, Je (x, t), into space plane, i, depends on fluxes in and out of, NN planes, i+1, and, i-1. The fluxes are for 2D-densities, n(i+1) , and, n(i-1) [particles.cm-2]:
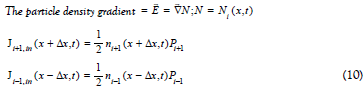
Factor ½ denotes the equal probabilities that a particle located at virtual plane, i, hops instantaneously into virtual plane, i+1 (right), and, i-1 (left), in 1D-space. Invoking particle flux conservation, the probability rate, as a hop-attempt frequency, is:

with τR representing a particle residence time within its spatial coordinate. The net particle flux across the virtual area, A, at x is:
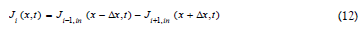
A first-order Taylor expansion of n(i+1) and n(i-1) in Eq (10) yields, to order Δx [particles.cm-2.s-1]:

Given that ni (x,t) / Δx=Ni (x,t) [particles.cm-2], a characteristic particle velocity is defined as:

This enables a physical interpretation of the particle kinetics in an interacting ensemble. Grossing defined quantum potential, up, to mean the “osmotic velocity” arising from the momentumfluctuating component of particle mass, mp [15]. This is responsible for the dissipation of energy as thermal outflow [14]. If in Eq (13) subscript, i, is replaced with subscript, p, the particle diffusive flux is:

where L=Δx= the effective distance travelled by a particle in time, τR. Incorporating Eq (3) into Eq (8) which is the net particle number entering the virtual space, dV=Adx, in time, dt, including particle loss due to energy dissipation in, dV, yields:
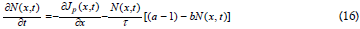
Assuming thermal conversion and dissipation is due to momentum fluctuations, the particle density losses act as the non-equilibrium thermodynamic source as described in the vacuum fluctuation theorem [17].
Finally, inserting Eq (15) describing particle diffusive flux into Eq (16) and equating the characteristic hopping and residence times, τ=τR, gives the non-linear logistic particle diffusion
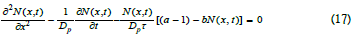
Non-linear particle density diffusion equation solutions by diffusion wave harmonic spectra
Solutions to Eq (17) depend on the physical process kinetics for a given particle ensemble, especially explaining how thermal and particle diffusion waves or oscillations generate harmonic patterns resulting in the observed particle masses. Consider a “core” (basic or fundamental) quantum field initially without any thermal or particle activities, then harmonic thermal energy dissipation occurs if the core quantum field is treated as a single-atom heat engine occluding resonant thermal energy which increases the local environment’s entropy [18-20]. Grossing also confirmed that single particles acted as periodic thermal dissipative systems in a non-equilibrium steady state by a “hidden” energy source [17]. The energy or heat source maintains heat exchange between a particle and its environment as a dynamic non-equilibrium thermodynamic process [21, 22]. Grössing formulated a conventional diffusion equation for the particle density (a probability density) with particle diffusivity:

mp=particle mass; E=ÃÂ?§ ω is the particle wave energy which gives rise to the fluctuating osmotic velocity. He showed also that the Schrödinger wave equation is derived from classical physics as well as from conventional quantum mechanical principles. However, the analogy with propagating wave fields is only for mathematical convenience [18]. When treated with eigenvalue equation methods, thermal waves cannot sustain spatially propagating eigen function solutions. These solutions are inconsistent with spatial damping, a hallmark of diffusion wave processes, due to leaky modes which result in the localisation of such fields within a diffusion length. Grossing did not connect the role of particle masses with fluctuating momentum to thermal wave evolution under equilibrium or dynamic steady state conditions. Similar caveats apply to other similar models [21-23]. The conversion of particle wave energy to thermal diffusion wave energy occurs when heat from a thermal source excites a particle. Then the particle acts as a heat engine producing oscillations at its mass resonance frequency. This mechanism dissipates energy as thermal oscillations, increasing the entropy of the surrounding environment [17, 20]. Internal particle energy conversion to thermal diffusion waves is a two-step process. Firstly, Eq (17) solves the spectrum of particle distributions obeying the non-linear logistic particle density diffusion equation. Secondly, the thermal content of each distribution is derived from associated thermal wave distribution fields.
From Eq (17) time periodic solutions are determined by introducing a Fourier series at a fundamental oscillation angular frequency, ω0 , and its harmonics:

Each harmonic order must be solved separately, with the solution for the adjacent next lower order acting as the input to the next higher order. Inserting Eq (19) into Eq (17) yields an infinite series of harmonic order solutions, compacted as:
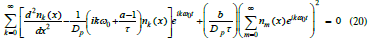
The solution is a series of infinite coupled equations with each term set to zero while coupled to lower orders through the non-linear term. The particle diffusion length, 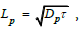 for the dc terms when k=m=0 in Eq (20). Thus for only time-independent dc and fundamental (first harmonic) terms, the following equation is obtained:
for the dc terms when k=m=0 in Eq (20). Thus for only time-independent dc and fundamental (first harmonic) terms, the following equation is obtained:
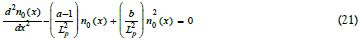
The solution is obtained by multiplying all terms by dn0(x)/dx, integrating, and using standard tables [24]:
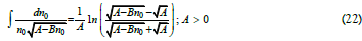
A>0 leads to a>1 satisfying the non-extinction condition of the particles’ population which is 1< a<4 Eqs (2 & 17); [8, 9].
The exact solution for the time-independent particle distribution, with the boundary condition n0(0) = N is:
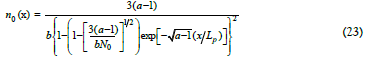
At an infinite distance away from the thermal source, the particle distribution is:

This is a non-zero, uniform (homogeneous) particle density directly linked to the environment’s background thermal energy. Under these conditions, thermophoresis, a phenomenon causing particle-toparticle attraction, is established. This is crucial to maintaining the particles together as an interacting ensemble [25-32].
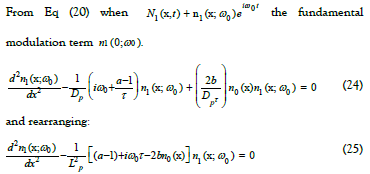
Eq (25) has no analytical solutions. However, 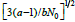 in the Eq (23) denominator is small since N0 at the origin is large [32].
in the Eq (23) denominator is small since N0 at the origin is large [32].
When we set 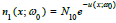 and use the WKBJ methods an approximate equation is obtained:
and use the WKBJ methods an approximate equation is obtained:
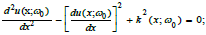
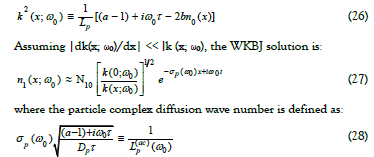
Eqs (27 & 28) show that the particle density distribution at the fundamental oscillation angular frequency, ω0 behaves like a mass diffusion wave, decaying exponentially with increasing distance from the particle source. The decay profile depends on the diffusion length, 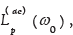 and the particle hopping time constant, τ. There is a phase lag (inertia) between the particle oscillation source and the mass diffusion wave propagation rate for angular frequencies,
and the particle hopping time constant, τ. There is a phase lag (inertia) between the particle oscillation source and the mass diffusion wave propagation rate for angular frequencies,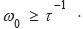 . The spatial range of the particle dc diffusive distribution, Lp, is different from, and independent of, the oscillating distributions at the fundamental frequency, f0= ω0 / 2π .The spatial diffusion lengths of dc and fundamental frequency (and higher harmonics) decrease with decreasing hop time, not. τ, and particle diffusivity, Dp, and increase with mass, m (Eq 18). The diffusion lengths also decrease with increasing oscillation frequency. The spatial separation of particles with different masses is enhanced by selective localisation based on different values of the product, ω0τ. Once the particles’ spatial separation is greater than the separation required for a given ensemble, then the particles are in a steady state with fixed mass values. The stable PDW status only holds when the non-equilibrium dynamics of the thermodynamic framework reach a steady state. It does not mean that a given particle is stable or unchanging.
. The spatial range of the particle dc diffusive distribution, Lp, is different from, and independent of, the oscillating distributions at the fundamental frequency, f0= ω0 / 2π .The spatial diffusion lengths of dc and fundamental frequency (and higher harmonics) decrease with decreasing hop time, not. τ, and particle diffusivity, Dp, and increase with mass, m (Eq 18). The diffusion lengths also decrease with increasing oscillation frequency. The spatial separation of particles with different masses is enhanced by selective localisation based on different values of the product, ω0τ. Once the particles’ spatial separation is greater than the separation required for a given ensemble, then the particles are in a steady state with fixed mass values. The stable PDW status only holds when the non-equilibrium dynamics of the thermodynamic framework reach a steady state. It does not mean that a given particle is stable or unchanging.
The non-linearity of the particle density diffusion equation Eq (17) generates solutions of diffusion wave harmonic spectra of all orders with respect to particle mass-specific momentum fluctuation frequencies. This introduces dc and ac particle diffusion lengths that control their density distributions as follows:
• The dc particle diffusion lengths give rise to the background densities and associated thermal contents. So the best observations are an average of all particle diffusion lengths resulting in an overall thermal content and temperature of an environment, and;
• The ac particle diffusion lengths give rise to selective spatial localisation and separation characteristics of each particle mass.
Particle density energy dissipation through thermal diffusion waves
In the quantum mechanical particle wave representation of spatial diffusion, the non-linear character of the logistic difference equation Eq (3), leads to the diffusion equation Eq (17). In an ensemble this creates an infinite spectrum of particle densities at all harmonics of the fundamental oscillation frequency, including the timeindependent dc term. Regardless of the specific thermal dissipation mechanism in any environment, the thermodynamic quantum potential shows that thermal diffusion takes place at the rate of particle diffusion [15]. Therefore, particle-driven thermal diffusion can be described using particle density energy sources and thermal diffusivity, DT=Dp [Eq (18)]. On this basis:
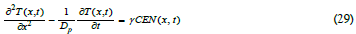
where N(x,t)=particle density, {Eq (19}; C=proportionality constant including the particle’s effective thermal conductivity or heat distribution, E=internal particle wave energy; N(x,t)hω total energy density where 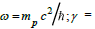 energy conversion energy particle energy into heat (non-radiative quantum yield). Letting
energy conversion energy particle energy into heat (non-radiative quantum yield). Letting 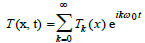 and substituting Eq (19) into Eq (29)’s source terms produces:
and substituting Eq (19) into Eq (29)’s source terms produces:
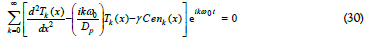
This is the complete thermal diffusion wave spectrum of particle ensemble temperatures. Therefore, for all orders of k, the associated thermal diffusion wave equation is:
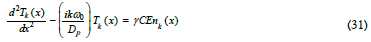
and each spatial component of the temperature spectrum is related to the full temperature field of harmonic, k , by:
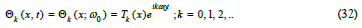
The linearity of Eqs (29) and (31) means that non-linear elements enter only through the spectrum N(x, t) of particle diffusion waves.
Two particular solutions for Eq (31) are explored as follows: the dc thermal diffusion (k=0); and, the fundamental thermal wave (k=1).
Thermal diffusion wave solutions
DC Thermal diffusion (k=0) solution
Eq (31) is solved from the time-independent particle distribution solution {Eq (23)}. Since N0 is large, then 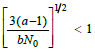
and, with a Taylor expansion of the denominator and retention of the first term, gives:
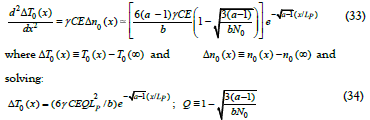
Taking the diffusivity of particles with mass, mn, from Eq (18), then the relationship between particle mass and thermal diffusion at location x=0 becomes:

The temperature rise of particles with mass, mn, is related to the thermal energy, U, obtained from an external source or by conversion of a fraction of the internal energy:

where cn=particle specific heat.
Assuming several core particles are present in the 1D-space, then all the masses and the thermal diffusion fields establish interacting ensembles based on the PDW hypothesis is complemented by the associated thermal wave (Thermon) henceforth redefined as Thermon-PDW Hypothesis. Consider several core particles within an ensemble, then for particles, n, of ensemble density, N(x,t), and mass, mn, harmonic oscillations at angular frequencies, kω0, occur [15]. If other particles with mass, mk, join the ensemble then similar harmonic decomposition excitation occurs. In the Grossing representation of momentum-mediated thermal dissipation, particles of mass, mk, dissipate energy:
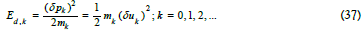
where k = 0 denotes the fundamental oscillation frequency; 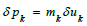 particle fluctuating momentum component; δuk=harmonic fluctuation of the characteristic particle velocity {Eq (14)}. Oscillations at harmonic frequencies, ωn=nω0 imply particle energies, En=nE0. Thermal harmonic oscillator characteristics are outlined later. Assuming similar particle velocity fluctuations - an assumption that is confirmed with the experimental data below - the proportional energy dissipation, δEn=nδE0 from Eq (37) implies the mass relationship mn - =nm0; n=1, 2,…. As a consequence of harmonic decomposition, the fundamental oscillation of a particle of mass mn=nm0 is excited at ωn =nω0, where ω0=fundamental oscillation angular frequency of particle mass m0. Therefore, for an ensemble, all the particles oscillating at ωn include particles of mass mn oscillating at the fundamental frequency and particles of mass m0 oscillating at the nth harmonic. The former particle density always dominates since, as the Fourier coefficient nk(x) in Eq (19) shows, the harmonic decomposition magnitudes decrease rapidly with increasing oscillation frequency. Invoking the Parseval relation associated with the Fourier spectrum of Eq (19) ensures that the system’s total energy remains finite and equal to the initial value as a necessary condition. If the integral mass relationship, mn=nm0, is assumed, the Thermon- PDW hypothesis predicts that ensemble particles oscillate and dissipate thermal energy at fundamental angular frequencies, coinciding with the harmonic multiples of the smallest mass fundamental frequency. The hypothesis does not claim that the same particles are always in a given location. But, there is always the same density of fixed mass particles in the environment. This density is precisely dependent on the particle diffusion amplitude and the thermal diffusion length, at a defined frequency. Conversely, for resonant harmonic oscillations excited by thermal absorption from fluctuating thermal sources, the higher resonant angular frequency oscillations are associated with the smaller masses [30,31]. In a simple classical mechanical oscillator model, in which
particle fluctuating momentum component; δuk=harmonic fluctuation of the characteristic particle velocity {Eq (14)}. Oscillations at harmonic frequencies, ωn=nω0 imply particle energies, En=nE0. Thermal harmonic oscillator characteristics are outlined later. Assuming similar particle velocity fluctuations - an assumption that is confirmed with the experimental data below - the proportional energy dissipation, δEn=nδE0 from Eq (37) implies the mass relationship mn - =nm0; n=1, 2,…. As a consequence of harmonic decomposition, the fundamental oscillation of a particle of mass mn=nm0 is excited at ωn =nω0, where ω0=fundamental oscillation angular frequency of particle mass m0. Therefore, for an ensemble, all the particles oscillating at ωn include particles of mass mn oscillating at the fundamental frequency and particles of mass m0 oscillating at the nth harmonic. The former particle density always dominates since, as the Fourier coefficient nk(x) in Eq (19) shows, the harmonic decomposition magnitudes decrease rapidly with increasing oscillation frequency. Invoking the Parseval relation associated with the Fourier spectrum of Eq (19) ensures that the system’s total energy remains finite and equal to the initial value as a necessary condition. If the integral mass relationship, mn=nm0, is assumed, the Thermon- PDW hypothesis predicts that ensemble particles oscillate and dissipate thermal energy at fundamental angular frequencies, coinciding with the harmonic multiples of the smallest mass fundamental frequency. The hypothesis does not claim that the same particles are always in a given location. But, there is always the same density of fixed mass particles in the environment. This density is precisely dependent on the particle diffusion amplitude and the thermal diffusion length, at a defined frequency. Conversely, for resonant harmonic oscillations excited by thermal absorption from fluctuating thermal sources, the higher resonant angular frequency oscillations are associated with the smaller masses [30,31]. In a simple classical mechanical oscillator model, in which 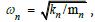 where kn=effective spring constant of the particle heat source, the relationship, mn=m0/n2, is easily deduced for constant, kn, at all resonance conditions. Within the Thermon-PDW model’s nonlinear wave oscillations, the particle mass relationships are resolved using Eqs (35 & 36). If all particles have identical specific heats based on equal quantum mechanical degrees of freedom, Eq (36) becomes:
where kn=effective spring constant of the particle heat source, the relationship, mn=m0/n2, is easily deduced for constant, kn, at all resonance conditions. Within the Thermon-PDW model’s nonlinear wave oscillations, the particle mass relationships are resolved using Eqs (35 & 36). If all particles have identical specific heats based on equal quantum mechanical degrees of freedom, Eq (36) becomes:
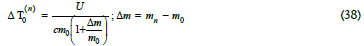
In a heterogeneous ensemble, the mass m0 is either the smallest particle's mass or the mass of the particle oscillating at the lowest resonant angular frequency, ω0. Introducing Eq (35) into Eq (38) gives a general relationship between particle mass, mn, and thermal diffusion field, T0, generated by dissipated heat transported through time-independent (steady state) particle diffusion:
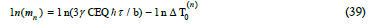
From the momentum-mediated thermal dissipation representation and the integral mass relationship, Eq (39) becomes:
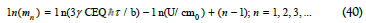
From the resonant frequency oscillation representation, Eq (40) yields the mass order relationship:
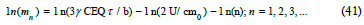
In the expressions Eqs (40 & 41), integers, n, represent increasing mass orders, mn. For both relations, parameters in the first two terms on the right-hand side are considered constant and independent of mass order. The relationships involving dc (time-independent) thermal and particle diffusion distributions are derived from the entire harmonic spectrum of oscillations since this is imposed by Eq (17), that is, the linked non-linear logistic thermal and particle density diffusion wave equation. Independent experimental results for particle masses (Figure 1) support mass order relationships, as determined from Eq (41) [2]. In Eq (40) increasing mass order, n, is the same as SRN. The experimental ln-linear mass relationship is fully consistent with the theoretical momentum-mediated thermal dissipation assumptions of particle velocity, harmonic fluctuation, independence from the oscillation frequency as developed in Eq (1) through to Eq (41). So the prime conclusion is that the Thermon-PDW model defines the SM particle distribution. It is the quantum mechanism which explains the relative mass values and should signpost a way to obtain the necessary quantitative data to determine the absolute values.
Fundamental thermal wave solution (k=1) for eq (31)
The thermal diffusion wave solution, given for k=1 by Eq (31) and for n1(x) by Eq (27), is derived as an integral with no analytical form. Since the exponential spatial profile of Eq (27) is the main, rapidly-ωο) decayincan be g factor, ignored. Thus the slow-decaying an approximate spatial analytical solution dependence, 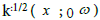 can be ignored. Thus an approximate analytical solution is:
can be ignored. Thus an approximate analytical solution is:

Using Eq (42) as the driving function, the Eq (31) solution is a combination of spatial thermal and particle density waves:

where: A is uniquely determined by the boundary condition ΔT1 (0) = T10 at the particle’s location. Using Eq (28) for σp, the solution for the fundamental thermal wave associated with the particle oscillation, is:

Note that the iω0τ factors cancel out in the denominator 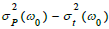 in Eq (43a) for a particle density diffusion length which controls the thermal diffusion length. In these circumstances, the resulting thermal wave expression {Eq (44)} becomes proportional to
in Eq (43a) for a particle density diffusion length which controls the thermal diffusion length. In these circumstances, the resulting thermal wave expression {Eq (44)} becomes proportional to 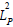 as in the dc term ΔT1(0) {Eq (35)}. Therefore, Lp emerges as the overall characteristic diffusion length for both thermal and particle diffusion processes.
as in the dc term ΔT1(0) {Eq (35)}. Therefore, Lp emerges as the overall characteristic diffusion length for both thermal and particle diffusion processes.
Further consideration of the thermal and particle diffusion wave equations
Thermal and particle diffusion in a single particle in a static state.
Hypothetically consider that random particle diffusion occurs in a single particle isolated from all adjacent particles. The combination of particle mass diffusion and random walk results in a stationary Gaussian spatial distribution of diffusion probability [26]. A similar conclusion is reached from a spatial 3D-diffusion model, but, for mathematical simplicity, a 1D approach is used, implying that the probability for net particle transport to a neighbouring spatial location=0, with Pi=v=0. From Eq (8), the net particle flux, Je, becomes a time independent constant as:

This means that the probability maximum of finding the particle is localised always at the same peak position and is independent of the number of excursion forays. There are two consequences depending on the observer’s location. An “internal observer”, within the reference frame of the particle, perceives an increasing probability of the mass spreading into adjacent locations with successive forays [26]. The internal observer can register these changes as a change in time. Previously this was defined as intra-time [5]. Conversely for an “external observer”, the physical interpretation of Eq (45) is that a particle’s distribution is static and its position is stationary . An external observer is unable to register intra-time, which might be equally defined as “hidden universe time”. Assuming that a drift force acts on the single particle, then, as expected, the probability peak for the particle at a location changes. Even then, an internal observer registers hidden time passing, but an external observer, still without a frame of reference other than the particle itself, fails to measure time.
The physical reality of a single particle’s diffusion and random walk is fully consistent with time independence as proposed by the Thermon- PDW hypothesis and the residence time constant, τR=1/v=∞ {Eq (11)}. A static state particle exhibits no spatial transfer rate, up=0 {Eq (14)}, and thus no diffusion capability, Dp=0 {Eq (15)}. These conditions have important energetic consequences. If thermal dissipation from a single particle is momentum mediated, which is consistent with the experimental findings (Fig 1), Eq (37) immediately yields Ed,k = 0; k = 0, 1, 2, …. This means that there is total absence of mass and thermal oscillations at any and all modes, including the dc, fundamental and higher harmonics. The model contains within it the conditions for a mechanism which supports assumptions made for the inception of free particle mass and indeed the whole universe.
The physical reality changes radically once a second particle emerges either in the same local environment as the first particle or arrives at the first particle’s location. In these circumstances the probability, Pi, is redefined as an attempt frequency 0 ≠ v for the particle position, i, to drift to a new position, (i ± 1), in relation to the first particle. It also means that the hidden time in the original single particle is revealed by particle drift. Both particles contribute to a net mass transfer giving meaning to residence time, τR = 1/v {Eq (11)}, and defining particle diffusivity through L= Δx{Eq (15)}.
Additional particles complete the diffusion formalism and, modifying the model for 3D-space, particle residence time eventually reaches a maximum, τR, f, at a steady state corresponding to particle density above which all particle diffusion within the local environment containing the participating particles occurs with the same probabilistic time constant. Under these conditions an external observer measures steady state particle-to-particle diffusion, Dp>0 {Eqs (17 & 18)}. This subsequently gives rise to momentum mediated thermal energy dissipation, diffusion and oscillation {Eqs (29 & 30) and Eq (38)]. If the same conditions apply in an environment which is the whole universe then the time measured is Universe Time (UT).
Two particle diffusion and drift defines the onset of universal time
Important quantum conditions drive thermal dissipation between two or more particles in adjacent locations, i and i ± 1 with a heat source. Coupled Thermon-PDW interactions establish a diffusive density leading to the onset of thermal oscillations and energy dissipation [27]. Fluctuation theorems show that macroscopic irreversibility arises from time-reversible microscopic dynamics [28]. For example, one irreversibility process known to generate thermal forces in particles, is diffusion by non-uniform random walk, enabled by Brownian motion randomness [28]. This can be seen in an ensemble of particles subjected to a non-Fickian diffusive flux. The superposition of diffusion and random walk becomes a Fickian flux {Eq (15)} with a temperature gradient produced by non-linear particle density and thermal diffusion wave oscillations. The combined mass and temperature gradient fields, first observed in fluid salt solutions, describe thermophoresis in fluids [29-31]. Under these conditions Eq (15) is replaced by the particle flux under thermal non-equilibrium in 1D-space:
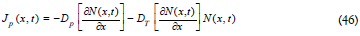
where DT=effective thermal diffusion coefficient [cm2.s-1.K-1] and 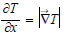 temperature gradient between the ensemble’s particles. The non-linear particle density diffusion (Eq (17)) is now replaced by:
temperature gradient between the ensemble’s particles. The non-linear particle density diffusion (Eq (17)) is now replaced by:
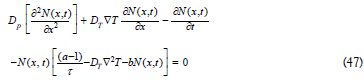
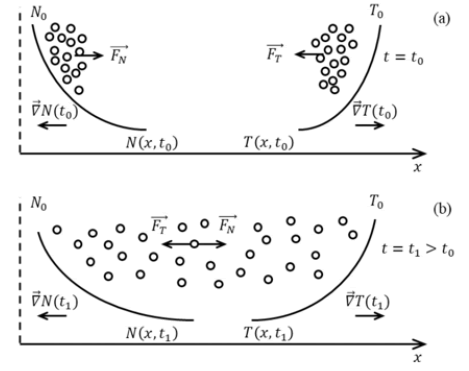
The particles are affected by two forces: one due to the density gradient; and the other due to the temperature gradient (Figure 6a & 6b). The forces act either in the same or opposite direction.
By simplifying Eq (47) (approximately valid for linear and mild temperature gradients), UT appears when the non-linear term bN2( x, t) and the ∇2T term are neglected. Under these conditions an analytical solution (analogous to the equation for charge drift in an electric field is [33].
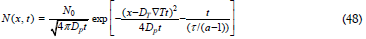
So, if a thermal gradient field is applied along the motion coordinate of ensemble particles, N0, the ensemble moves towards the low temperature end of the thermal field with a drift velocity of:

The negative sign indicates that the drift motion is in a direction opposite to the thermal gradient (Figure 6). This is consistent with statistical thermodynamics as the frequency of particle hops increases with increasing thermal energy supplied by a heat source or particle thermal dissipation sources {Eq (23)}. At the same time, ensemble particles diffuse away, due to random motion, as from a heat source in isothermal equilibrium of ∇T = 0 (Figure 6b).
For an external observer physically able to measure particles, the drift motion from one location to another due to a thermal gradient, is equivalent to UT.
The drift, Δx , of the particle’s peak distribution is:

Thus Eq (50) gives the minimum time, ∇tL , required for a particle at location, i , to travel a distance, x = L , to the location of an adjacent particle, i ± 1 .
Particle diffusion and non-uniform random walks, in a thermal gradient, gives rise to thermophoresis. This directly leads to the explicit, sequential emergence of time. This also applies to a two particle (or more) ensemble {Eq (48)}, where N(x,t)=occupation probabilities (1,1), (2,0) or (0,2) between adjacent sites, i and i ± 1 . Thermal kinetic exchange between two (or more) particles explains an external observer’s perception of relative motion and so the passing of UT. Finally, note that the same physical analysis for Eq (48) also applies to a single particle. However, an external observer, lacking a frame of reference, cannot measure the variation of x for Eq (50) and is unaware of UT passing.
Thermal dissipation calculations for the complete non-linear Eq (47) with mild temperature gradients, follows the same mathematical development of Eqs (19 to 28) and (30 to 31). This generates a zeroth order particle density equation to replace Eq (21) which, if b<<1, yields a diffusive term:
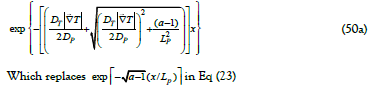
Eq (50a) highlights the major role thermal gradients play in the spatial diffusion and particles’ drift by shortening the diffusion length,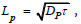 of a mixed thermal and particle diffusion drift length, LM, defined as
of a mixed thermal and particle diffusion drift length, LM, defined as
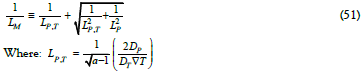
A similar mixed diffusion drift length prevails in thermal wave oscillations of interacting particles. Significantly, thermal diffusion wave fluctuations associated with particle density diffusion and random walk are energy dissipation mechanisms which lead to regional universal temperature gradients {Eqs (20 & 23)}.
The emergence of UT is determined by the rate of the particles’ drift relative to their original locations. In turn this leads to particle distribution probability drift which for an external observer enables measurement of UT anywhere in the universe {Eq (50)}.
Thermodynamic framework
The new Thermon-PDW hypothesis drew our attention to important antecedents, reawakening earlier disagreements about quantum physics, especially its division into discrete fields or missing factor(s) [35]. Bohm concluded of individual systems at a quantum level of accuracy” is possible [35]. De Broglie recognised the importance of the wave structure of matter about 100 years ago, eventually proposing that there were missing factors based on, !the hidden thermodynamics of particles” [21, 35]. These ideas were neglected for lack of evidence [36, 37]. The inability to conceive of the Thermon-PDW model was inevitable since, in De Broglie’s era, at least 10 free SM particles were unknown. De Broglie, Bohm and others were frustrated by their inability to demonstrate the proper (possibly overarching) significance of all thermodynamic principles within quantum physics. The wider scope of the Standard Model of particles may be fulfilled by the Thermon-PDW model which gives the complete thermodynamic framework.
Pre-particle mass framework
The model initially assumes an ensemble of pre-particles in a 1Dspace, but simply extends to 3D-ensembles in universe space. Nonlinear logistic thermal wave and classical particle diffusion wave solutions based on pre-particle momentum (given by particle hopping and residence times) are straightforward from Eqs (1 to 17). As steady state non-linear conditions are established within an ensemble, the mechanism preserves the expected number of different SM particles with the observed relative masses. Local particle distribution changes, due to either particles entering or exiting an ensemble, are made to restore restored to the expected values by the imposed equilibrium state. Observations are presently limited in the absence of quantitative SM particle distribution frequ--encies, and experimental confirmation that pre-particles have the same mass as their respective SM particle masses determined by experimental. Observational data for the 12 particle lepton and quark SM subgroup (excluding bosons, photon & gluon) show that ln mass is linearly correlated with SRN for the 12 particles, such that the masses are a precise harmonic sequence (Figure 1), expressed within the general framework of quantum probabilities [23]. This is achieved by treating all pre-particles as thermal sources, either as heat engines or recipients of external environmental heat, resulting in the generation of diffusion-wave harmonic spectra for all orders of all mass specific momentum fluctuation frequencies of particles {Eqs (18 to 28)}. Alternatively, pre-particles generate thermal diffusion waves giving an infinite spectrum of particle density ensembles at all harmonics of the fundamental oscillation frequency. Steady state thermal energy source conditions create a stable mix of SM particles {Eqs (29 to 32)}. These conclusions come from modelling physical reality in a local environment, but there is no theoretical or physical impediment to extending the local environment expectation to the whole universe, as noted in several instances, with further implications discussed elsewhere [38].
Thermophoresis
The local stability of ensembles is of interest, particularly because mutual interactions between quantum fields assist the formation of harmonic thermal fields, which are obligatory for the inception and stability of SM particles. The particle-to-particle attraction mechanism is due to non-linear thermal diffusion waves and is termed “thermophoresis” by analogy to similar physical processes already observed in molecular systems (Figure 6). From the initial stages of thermal flow to the maximum steady state level, thermophoresis increases from zero to the maximum level. Although the quantitative magnitude is unknown, we suggest it is a significant factor which is discussed elsewhere with other Thermon-PDW activity, particularly as a quantum mechanisms which contribute to gravity [38-40].
Conclusions
Other conclusions and comments
• The time-independent particle distribution solution {Eq (23)} predicts ensembles containing pre-particles at harmonic multiples of the lowest particle frequency {Eqs (33) to (41)}. This guarantees that there is always a fixed, finite particle density for particular diffusion waves and thermal diffusion frequencies, {Eq. (40)}. Similarly, resonant frequency thermal oscillations correlate directly with increasing pre-particle mass. In both cases these physical events arise from the complete harmonic spectrum of oscillations imposed by the non-linear nature of the fundamental hypothesis {Eq (17)}.
• The fundamental thermal wave solution {Eqs (42 to 44)} directly correlates the model’s particle mass and thermal wave energy dissipation with the experimentally observed SRN {Eq (41)}. The theory supports the crucial role of thermal diffusion waves as an efficient mass separation and identification mechanism within an ensemble of different pre-particles by particle dissipation energy, Ed, and mass order across all harmonic thermal wave oscillation degrees of freedom available. The non-linear particle and thermal diffusion wave model of energy emission represents a standard harmonic series dividing the total particle density into a series of constituent densities, each oscillating at the fundamental angular frequency, and higher harmonics, where n=2, 3, 4, … If the fundamental modulation frequency represents the particle wave fluctuation, from the rest energy En = mnc2 = nm0c2 = hc/λn and thus mn ∝ 1/ λn = n/λ0, then the harmonic ensemble consists of particle masses equal to integral multiples of the smallest mass m0. Alternatively for a mechanical resonance oscillation in a particle, the harmonic ensemble of particles resonate at integral multiples of the fundamental. The physical meaning is that a spatial network (distribution) of interparticle forces, Fn, forms with the effective spring constants linked to the weakest force, F0, such that kn = n2k0 . The simultaneous operation of both kn mechanisms is also possible, so that an ensemble of particles, whose masses are integral multiples of a fundamental particle mass, oscillates thermally exactly as if they were an ensemble of one particle species, thermally oscillating at all harmonics of that mass.
• Different SRN-harmonic correlations depend on harmonics favouring either the dc field or the particles excited at the fundamental frequency. This might explain the different boson alignment compared with the other elementary particles.
• The photon and gluon position appears anomalous since they are massless. One possibility is that the photon behaves as a photon gas which exerts radiation pressure on matter. In this case the photon carries an effective mass with its momentum and, in an oscillating thermal field, behaves similarly to particles with mass. Further reconciling the model with respect to quantum electrodynamics and general relativity has not been investigated to date. It has not passed unnoticed that the model generates hidden time and that time may be variable.
• Similarly the relationship with the Higgs boson has not been explored. It is noted that the Higgs particle carries a mass which may be derived from the Thermon-PDW mechanism. If the Higgs particle does perfuse the entire universe, the Higgs field would ensure transmission of thermal and diffusion waves throughout the universe.
Acknowledgments
A. Mandelis gratefully acknowledges the Natural Sciences and Engineering Research Council (NSERC) Discovery Grants Program and the Canada Foundation for Innovation (CFI) Research Chairs Program. J.H.O. Slater acknowledges funding from Advanced Physics Initiatives. We are most grateful to the following for advice: David Benton (Aston); Mark Fox (Sheffield); Colin Freeman (Sheffield); Katherine Freese (Michigan, Texas/Austin); Gerry Gilmore (Cambridge); Sheldon Goldstein (Rutgers); and Dave Newbold (Bristol, CERN).
References
- Tanabashi, M. et al. (Particle Data Group). Physical Review D, 98, (2018 and 2019 update), pdg.lbl.gov/2019/listings/rpp2019-list-electron.pdf, (2020).
- Gasiorowicz, S. & Langacker, P. “Elementary Particles in Physics”, pp. 48, www.physics.upenn.edu/~pgl/e27/E27.pdf, (2019)
- Blumhofer, A. & Hutter, M. Family structure from periodic solutions of an improved gap equation, Nuclear Physics B, 484, 80‑96, (1997)
- Griffiths, D. “Introduction to Elementary Particles”, Second Edition, Wiley·VCH v..bg GmbH & Co. KG, Weinhim, pp. 454, mikefragugliacom.files.wordpress.com/2016/12/introduction-to-elementary-particles-gnv64.pdf, (2008).
- Slater, J.H.O. https://researchers.one/articles/a-new-hypothesis-for-the-universe-the-role-of- thermal-gradients-in-setting-time-forming-three-dimensional-space-and-populating-with-matter- and-energy/5f52699c36a3e45f17ae7db8/v1, pp. 11, (2019)
- Senior, E., Bull, A.T. & Slater, J.H. Enzyme evolution in a microbial community growing on the herbicide Dalapon, Nature, 263, 476-479 (1976)
- Slater, J.H. Microbial population and community dynamics, “Microbial Ecology: A Conceptual Approach”, Lynch, J.M. & Poole, N.J. (Editors), Blackwell Scientific Publications, 45‑63, (1979)
- May, R.M. Simple mathematical models with very complicated dynamics, Nature, 261, 459–467, (1976)
- May, R.M. “Theoretical Ecology: Principles and Applications”, Oxford, Blackwell Scientific Publications, pp. 317, (1976)
- Ausloos, M. & Dirickx, M. (Editors). “The Logistic Map and the Route to Chaos: From the Beginnings to Modern Applications”, Springer, pp. 415, (2006)
- Verhulst, P‑F. Recherches mathématique sur la loi d'accroissement de la population. Mémoires de l'Académie Royale des Sciences et des Lettres de Bruxelles, 18, 1–38, (1845)
- Schrödinger, E. An undulatory theory of the mechanics of atoms and molecules, Physical Review, 28, 1049‑1079, (1926)
- Angström, A.J. (1861). Quoted in [14]
- Mandelis, A. Diffusion waves and their uses, Physics Today, 53, 29‑34, (2000)
- Grössing, G. On the thermodynamic origin of the quantum potential, Physica A, 388, 811‑823 (2009)
- Mandelis, A, Nicolaides, L. & Chen, Y. Structure and the reflectionless/refractionless nature of parabolic diffusion‑wave fields, Physical Review Letters, 87, 020801, 4 pages (2001)
- Grössing, G. The vacuum fluctuation theorem: Exact Schrödinger equation via non‑equilibrium thermodynamics, Physics Letters A, 372, 4556‑4563, (2008)
- Mandelis, A. “Diffusion‑Wave Fields: Mathematical Methods and Green Functions”, Springer‑Verlag, New York, pp. 741, (2001)
- Roẞnagel, J. et al Single‑atom heat engine, Science, 352, 325‑329, (2016)
- Pearson,. A.N. et al. Measuring the thermodynamic cost of timekeeping, Physical Review X, 11, 021029 1‑8, (2021)
- De Broglie, L. The reinterpretation of wave mechanics, Foundations of Physics, 1, 5‑15, (1970)
- De Broglie, L. The thermodynamics of the isolated particle, “The Great Problems of Science” Fevrier, P. (Editor), Delphnich, D.H. (Translator), Gauthier‑Villars, Paris, 1‑98. (1964)
- Bohm, D. A. Suggested interpretation of the quantum theory in terms of “hidden” variables. I, Physical Review, 85, 166–179, (1952)
- Gradshteyn, I. S. & Ryzhik, I. M. “Table of Integrals, Series and Products”, Academic, New York, p. 73, entry 2.224.5, (1980)
- Pearson, K. The problem of the random walk, Nature 72, 294, (1905)
- Crank, J. “The Mathematics of Diffusion”, Oxford Scientific Publications, Oxford, pp. 421, (1979)
- Kim, Y‑J. Einstein’s random walk and thermal diffusion, arXiv:1307.4460, (2013)
- Williams S. R., Searles, D. J. & Evans, D. J. Independence of the transient fluctuation theorem to thermostatting details, Physical Reviews E, 70, 066113 1‑6, (2004)
- Ludwig, C. Diffusion zwischen ungleich erwärmten Orten gleich zusammengesetzter Lösungen, Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften: Mathematisch‑Naturwissenschaftliche Classe, 20, 539 (1856)
- Piazza, R. Thermophoresis: moving particles with thermal gradients, Soft Matter, 4, 1740–1744, (2008)
- Tiwari, P., Antal S. P. & Podowski, M. Z. Modeling shear‑induced diffusion force in particulate flows, Computers & Fluids, 38, 727–737, (2009)
- McKelvey, J. P. “Solid State and Semiconductor Physics”, Harper & Row, New York, Section 10.3, 340‑341, (1966)
- Becker, A. “What is Real?: The Unfinished Quest for the Meaning of Quantum Physics”, John Murray, London, pp. 370, (2018)
- Bohm, D. A. Suggested interpretation of the quantum theory in terms of “hidden” variables. II, Physical Review, 85, 180–193, (1952)
- De Broglie, L. “The Wave Nature of the Electron”, Nobel Lecture”, p 244-256, (1929).
- Feynman, R. “Six Easy Pieces: The fundamentals of Physics Explained”, Penguin Books, London, pp. 146, (1999)
- Susskind, L. & Friedman, A. “Quantum Mechanics: The Theoretical Minimum”, Penguin Books, London, pp. 364, (2014)
- Mandelis, A. & Slater, J.H.O. A new cosmological model: inception and maintenance of the universe. Journal of Pure and Applied Mathematics, in press (2023)
- Požar, T. et al. Isolated detection of elastic waves driven by the momentum of light, Nature Communications, 9, 3340, (2018)
- Bass, S.D., De Roeck, A. & Kado, M. The Higgs boson implications and prospects for future discoveries. Nature Reviews Physics, 3, 608–624, (2021).