Use the Schwarzschild metric to calculate the proton-to-electron mass ratio

Received: 27-Mar-2023, Manuscript No. puljpam-23-6275; Editor assigned: 29-Mar-2023, Pre QC No. puljpam-23-6275 (PQ); Accepted Date: May 29, 2023; Reviewed: 30-Mar-2023 QC No. puljpam-23-6275 (Q),; Revised: 31-Mar-2023, Manuscript No. puljpam-23-6275 (R); Published: 31-May-2023, DOI: 10.37532/2752-8081.23.7(3).143-145

Citation: Cheng Z. Use the schwarzschild metric to calculate the proton-toelectron mass ratio. J Pure Appl Math. 2023; 7(3):143-145.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Abstract

This paper attempts to apply the Schwarzschild metric of the gravitational field to the electromagnetic field to obtain a Schwarzschild radius in an electromagnetic field. According to this radius, microscopic space-time can be divided into two parts, the real space-time outside the radius of the electromagnetic field Schwarzschild, and the virtual (or imaginary) space-time within the radius. The properties of these two space times are exactly similar to the space time features inside and outside the radius of the event horizon in gravitational black holes. Combined with virtual space time-based particle models and the latest experimental data on proton electromagnetic radius, we can calculate a more accurate proton-to-electron mass ratio.

Keywords

Metric; Proton-to-Electron; Mass; Ratio

Introduction

The Einstein tried to unify gravitational and electromagnetic interactions. Based on Einstein's profound insight into the laws of physics, his idea should still contain very deep meaning. It's just that our ability to think is not as cognitive as Einstein's, so many times we think that this is not feasible.

There are many similarities of gravitational interactions and electromagnetic interactions. The main manifestation is that both show an inverse square relationship. In addition, there is now enough evidence to suggest that both electromagnetic and gravitational interactions are related to changes in space-time. If we accept that gravitational interactions are caused by the bending of space-time, then electromagnetic interactions that are stronger than gravitational interactions can also cause space-time bending. In this way, we can also use the curvature of space-time to represent the existence of electromagnetic interactions.

We can also note that gravitational and electromagnetic interactions produce the same effect of exerting force. This is also the basic principle of the current maglev train.

And in the spherically symmetric gravitational field, we already have a very concise Schwarzschild solution. This paper introduces the Schwarzschild solution of the gravitational field into the electromagnetic field, so that a spherically symmetric electromagnetic field metric similar to the Schwarzschild metric can be constructed. This electromagnetic field space-time metric can be used to describe the bending effect of electromagnetic interactions on space-time.

Spherically symmetric electromagnetic field space-time metric

Let's start by listing the Schwarzschild metric so that we can compare them later.

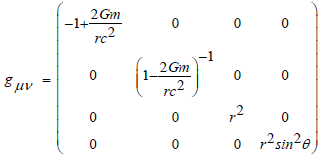
From the Schwarzschild metric, when

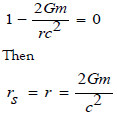
This radius is called the Schwarzschild radius.

Therefore, when constructing the space-time metric of the electromagnetic field, the main work is to construct a formula similar to the Schwarzschild radius in the electromagnetic field.

In the electromagnetic interaction column, similar to Newton's gravity, Coulomb's law is similar. Among them, Newton's law of gravity

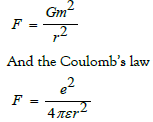
Comparing Newton's laws of gravity and Coulomb's laws, we can see that Gm² can be replaced by e² / (4πε) in Coulomb's law.

Now let's change the formula for the Schwarzschild radius slightly

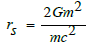
Following the above requirements, the corresponding terms are replaced, and finally we have the Schwarzschild radius formula for the electromagnetic field.

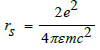
Since the mass m here is a relatively special mass, we can get it in ms terms

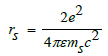
This way we can get the Schwarzschild metric of the electromagnetic field

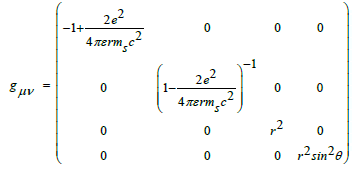
Event horizon boundary for electromagnetic fields

At the microscopic scale, if the radius is equal to the Schwarzschild radius of the electromagnetic field, we can find that spacetime is divided into two parts. Beyond the Schwarzschild radius is real spacetime. Within the Schwarzschild radius, it's virtual spacetime. This is consistent with the black hole solution of the gravitational field.

Since the spin velocity of the electromagnetic field is equal to the speed of light, it can serve as the boundary between virtual spacetime and time spacetime [1,2]. This radius can be calculated approximately equal to

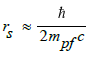
where mpf indicates the electromagnetic mass of protons caused solely by electromagnetic interactions.

Such

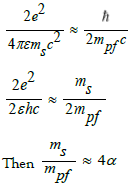
In addition, in the theory of virtual or imaginary spacetime, ms is the boundary mass between virtual spacetime and real spacetime [1, 2]. If the mass of electrons and protons has a symmetric relationship, the following relationship can be satisfied

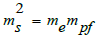
Then we can calculate the proton-to-electron mass ratio

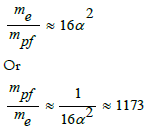
As can be seen from the calculations, this mass ratio is much smaller than the results measured experimentally.

Consider the energy of strong interactions

If we do not consider that protons contain internal structures, according to the theory of virtual spacetime, the electromagnetic radius of a proton is about 1.41fm [2]. This is larger than the currently accepted experimental value of 0.84fm [3]. This difference may be related to the energy generated by the strong interaction within the proton.

Here, the particle model based on virtual spacetime is improved according to the experimental measured electromagnetic radius [2]. For formulas

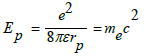
Since the mass of electrons is an experimentally measured value. Moreover, the electron mass is very light, and the electron does not participate in strong interactions, so the electron mass cannot be changed in the above formula. In this way, we can multiply by a factor g to reflect the change in electromagnetic radius due to the strong interaction. Namely

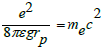
Since

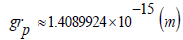
Substituting the experimental value of 0.84fm, it can be obtained

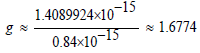
Considering that the electromagnetic mass is inversely proportional to the particle radius, this also means practical

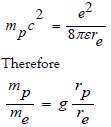
If the additional energy generated by the strong interaction is not taken into account at all, there should be

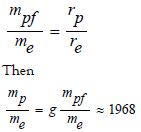
This is still relatively close to the experimental measurement.

Conclusions

How to unify electromagnetic interactions with gravitational interactions has always been a problem that Einstein pondered in his later years. One contribution of this paper is to apply the Schwarzschild metric in gravitational interactions to electromagnetic interactions, from which the similarities between gravitational and electromagnetic interactions can be seen.

In addition, from the calculations in this paper, it can also be seen that proton has an internal structure, and it is precisely because of this internal structure that there is a strong interaction, and this strong interaction will cause the mass of the proton to be measured and the result is greater than the mass obtained by the electromagnetic interaction. By using the electromagnetic radius value of the proton measured experimentally, and using it to correct the results calculated by the particle model based on Virtual Spacetime, a more accurate protonto- electron mass ratio can be obtained.

However, from the calculation results, the error is still relatively large, which also indicates that the structure of protons may be more complicated. There are many factors that can affect the mass of protons and electrons.

References

1. Cheng Z. Foundations of Virtual Spacetime Physics. LAP LAMBERT Aca Pub. 2019.[Google Scholar] 

   [Crossref]

2. Cheng Z. A Particle Model Based on Virtual Spacetime. Vixra. 2022. [Google Scholar] 

   [Crossref]

3. Li R, Sparveris N, Atac H, et al. Measured proton electromagnetic structure deviates from theoretical predictions. Nature.2022: 611;265–70.

   [Google Scholar]  [Crossref]