Vocal Tract Modeling using Digital Waveguide for 2D non-uniform Rectilinear Grid
Received: 08-Oct-2021 Accepted Date: Oct 22, 2021; Published: 29-Oct-2021
Citation: Mahar MMH. Vocal Tract Modeling using Digital Waveguide for 2D nonuniform Rectilinear Grid. J Pur Appl Math. 2021; 5(6):67:77.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
The structured and uniform meshing is the big limitation for the implementation of the two-dimensional digital waveguide model in the modelling of the vocal tract. In other word, the length of each edge of the mesh must be same to keep the same delay lines in the digital waveguide of the vocal tract meshing. The same approach with structured and non-uniform meshing has been used in the current work for the simulations of the two- dimensional waveguide modelling of the vocal tract. For this purpose, two types of delay lines are introduced with the coded names of smaller-and larger-delay lines. The larger-delay lines are chosen as the double of the smaller-delay lines and this approach leads to no need of fractional delays. The effective simulations of sound wave propagation in the two- dimensional waveguide modeling of the vocal tract are also given by this method. In the current work, the construction of the non-uniform rectilinear mesh is bases on the combination of larger-and smaller-delay lines. The vowel /ɔ, /ɑ/, /ɛ/, /i/ and /u/have been chosen for the demonstration of the proposed work. In all vowels of the current work, the central part of the meshing of the vocal tract has been taken with dense mesh while coarser mesh is implemented in the other parts of the meshing. For the validation of the proposed work, the standard two-dimensional waveguide model with the uniform grid is considered as our benchmark model.
Keywords
Digital wave guide; Vocal tract; Non-uniform rectilinear
Introduction
Current technologies-based speech generations are being used in many fields of life and get much focus by many researchers. In human being, speech is a most natural way to communicate with each other. Speech production technology is a challenging field of the research that has great contribution in human-machine interaction. The human being uses diagrams, written text messages, gestures by using the body language, figures, singing and articulate to communicate with each other. Today the speech technology is being extensively used in many different areas of our daily life. However, speech production is highly complex technique.
In the process of speech production in human being, the lungs push the airflow which passes through the glottis and it is modulated by the vocal tract. In final process, the airflow is radiated through the lips. Human speech system is divided by two basic subsystems such as vocal folds and vocal tract. The vocal folds generate the train of pulses under the pressure of lungs that is way vocal folds are termed as the basis of sound. The vocal tract imposes its resonance on the train of the pulses which is called the modulation of the vocal tract. The quality of the voice, which is a primary concern, relies on the form of the vocal tract in the speech production system. The vocal tract is assumed as a function that depend on the area around its mid line i.e. a function with a variation of the cross-sectional area. Both the vocal folds and vocal tract form the basis of the speech production model. The lungs are the first organ in the human speech production which push the airflow and passes through the glottis. The airflow comes from glottis is modulated by the vocal tract. In the last process, the airflow is radiated through the lips. However, in the human being, speech production model is simply divided into two basic subsystems. These two subsystems are known as vocal folds and vocal tract.
The vocal tract imposes its resonance on the train of the pulses which is called the modulation of the vocal tract. Many researchers paid much attention on the modeling of the vocal folds with some variations [1-11].
The quality of sound is linked to the shape of the vocal tract. The formation of the vocal tract in the speech modeling is supposed as the concatenation of cylindrical tubes of different in length with different cross-sectional area. In the literature, Numerous works with different variations have been dedicated to the modeling of the vocal tract [12-21]. In the wave guide model, the vocal tract is mapped on a regular grid where each node is a assumed as a scattering junctions connected by unit wave guide elements [22-25]. In the wave guide modeling of the vocal tract, the approaches of cylindrical segments [26] and conical segments [27, 28] are being used successfully for the simulation of the wave propagation. Kelly–Lochbaum was first to employ the approach of cylindrical segment which is known as one-dimensional wave guide model. Digital wave guide models are the extensions of the wave guide model and they are very popular due to its realistic and high-quality sound generation in real-time. Now a day, these models are frequently used in recent works such as [29-33]. A digital wave guide has also been used to model the vocal tract of animals in [34] and it was successfully implemented to reproduce sound effects of a lion’s roar and wolf’s growl. The Kelly Lochbaum model of the vocal tract was proposed on the basis of same-length tubes of different cross-sectional areas and some works have also been dedicated to modifying for bringing the better quality in the Kelly -Lochbaum model and it was done by taking fractional elongation of the lengths of the tubes.
When the quality of sound is prime concern, the standard two-dimensional wave guide model is good choice for the modelling of the vocal tract [35- 37]. However, the two-dimensional wave guide has a limitation of high computational cost as compared to one-dimensional wave guide model which is considered as computationally efficient. There are several others limitation of the wave guide models [38-40] in which the restriction on the uniform structured grid with the same gridlines is one of them.
In the current thesis, we are focused on the two-dimensional digital wave guide model of the vocal tract with the structured and non-uniform rectilinear grid of impedance mapped. We introduce two types of grid lines in which one is assumed as smaller grid line and other is considered as larger grid line. To avoid fractional delay, the larger-grid line is the double of smaller grid line. This eliminates the need to get interpolation for the approximation of fractional delay and give efficient simulation for sound wave propagation in the two-dimensional wave guide modeling of the vocal tract in the non-uniform grid. The combination of these two different grid lines in the meshing creates the scheme of the non-uniform rectilinear mesh. The present work is demonstrated on the vowel / ⊃, / α /, /ξ /, /i / and / u / [41].
Digital Waveguide Modeling of the Vocal Tract
One-Dimensional Digital Waveguide Model
In one dimensional wave guide model, there is a chain or series of a uniform cylindrical pieces for approximation of the vocal tract.In other words, the uniform cylindrical segments are used to form the vocal tract of different cross-sectional area in which the wave components are scattered and travelled with fixed delay line.With the help of the solution of wave equation, the relation has been developed between velocity and pressure in to the uniform tube [42].
The solution of wave equation for one-dimensional is comprised by the right and left traveling wave components. At the junction of i th and (j+1) th, the solution of continuity equation is formed as given below with coefficient of reflection ri,
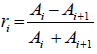
Where Ai is representing the cross sectional area of the tube. With the help of coefficient ri at the junction of two consecutive cylinder, scattering shows the propagation of wave in the vocal tract.
Two-Dimensional Digital Waveguide Model
With the help of increasing dimension of the grid, the accuracy for the solution of wave guide model can be increased. In the other words, the results of the one-dimensional wave guide can be obtained more accurate by employing extension in the wave guide structure which is called digital wave guide mesh. At each node of the mesh,one-dimensional wave guide model like technique is applied on the higher dimensional wave guide model to get the goal of digital wave guide modeling. The work of the current thesis is also on the two-dimensional wave guide mesh due to easy and simple configuration. In the two-dimensional rectilinear grid, each node has four neighboring junction that have equal distant form each side and has the angle of zero or 90 degree from central node.Figure 1 is shown the simple structure of rectilinear grid with multiple nodes.
Figure 2 shows the single junction with four neighboring junctions denoted by 1,2,3 and 4.There are two types of arrows represented by the figure one is horizontal and other is in vertical direction.The direction of arrows shows the direction of flow of pressure or the volume velocity. the arrival of the pressure or volume velocity at the junction is represented by the positive pressure while the leaving of the pressure or volume velocity is from the junction is denoted by the negative pressure.
The figure 2 shows the four neighboring nodes to the junction ‘J’ which are denoted by 1,2,3 and 4. The pressures at the neighboring nodes are denoted by 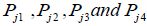 .
.
The negative pressure 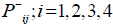 is used for leaving the nodes and the positive pressure
is used for leaving the nodes and the positive pressure 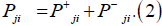 is used for arriving at the nodes. So, total pressure PJ,i is calculated as
is used for arriving at the nodes. So, total pressure PJ,i is calculated as
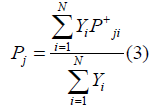
The total pressure ‘P’ at the junction ‘J’ for N ports is written as given below
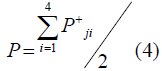
Where Yi is acoustics impedance in the channel.
In the proposed work each junction J has four neighboring junctions with assumption of homogeneous acoustics, then equation (3) may be written as.
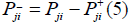
With the help of equation (2) the output going pressure can be calculated as
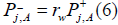
The waves that come from the boundary of vocal tract is scattered by the wall reflection coefficient rw and bounce back to the original mesh. For single node ‘A’ at the boundary of the vocal tract,
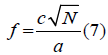
By using the distanced between to nodes, the sampling frequency fs dimensional N waveguide model [32], is formed for multi
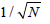
Where cis denoted by speed of sound.
In current work, the speed of sound c has taken 345 m/s, and the value of N has been taken as 2.In rectilinear mesh the distance between any two junctions has been taken four and sampling frequency is fs / 4
Non-Uniform Rectilinear Grid Meshing
There are various techniques used for modeling of vocal tract. A few of them are illustrated like as triangular, square, hexagonal, rectilinear, and tetrahedral for two- and three- dimension. The easiest topology for the modeling of vocal tract is rectilinear topology. With the help rectilinear topology the wave propagation form junction to its neighbouring through the distance 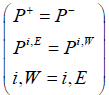 where N is number of dimension.In digital wave by model the path followed by which has always even or odd number of unit delays which followed to sampling frequency as fs / 4.
where N is number of dimension.In digital wave by model the path followed by which has always even or odd number of unit delays which followed to sampling frequency as fs / 4.
Now in current work we use rectilinear technique due to its simplicity. Now we use the technique to generate and implementation of non-uniform meshing grid as given in [43].By the help of this technique we can find less computational cost to find the format frequency. There are two types of grid lines in which one are smaller grid lines other are longer grid lines.Larger grid lines mean double of the smaller grid lines. These lines generate the two- dimensional rectilinear grid. By using this scheme we can find transfer function without fractional delay.
Figure 3 shows an example of the uniform rectilinear grid [44]. In this figure, simple topology is used. This mesh 10x11 ordered mesh with total nodes are 110. Each node in the grid shown by the integer from 1 to 110. In the above figure in which some nodes are boundary nodes that have three port junctions some are corner nodes that have only two port junctions. We see that all nodes have fixed and same length that behave as fixed sample delay for the propagation of wave.
In the Figure 4, we skip the nodes labeled as 12,14,16,32,34,36,52,54,56, 72,74,76,92,94 and 96.We observe that two types of squares are shown in the Figure 4 where one is large square and other is small square such that the small square is one fourth of large square. In the current configuration not all nodes are used to scattering of the propagation of the wave while some are only used to keeping tracking the movement of the wave. In the current mesh deleting nodes are named as Local nodes and all other are named as junction.
There are three steps to simulate the wave propagation in the vocal tract,firstly we find scattering of wave on each junction by using equation (4) and (5).
The movement of wave at each local node is done in second step which explain as.
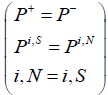 for each local node in horizontal direction (7)
for each local node in horizontal direction (7)
 for each local node in vertical direction (8)
for each local node in vertical direction (8)
where i denotes the local nodes and E,W , N , S are East, West, North and South respectively.
In the last step the propagation wave comes from neighbour junctions and we pass the delay at each node.
If di is the length of consecutive three nodes for example 23, 33 and 43 in the grid and ds is the length of small edges between 28 and 38 as shown in the Figure 4.
di = 2ds (9)
In current work sampling frequency fs is obtained by the smallest distance “ds ”
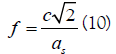
Where c is defined earlier.
In the previous work, the non-uniform mesh was generated by designing of dense mesh along the wall boundaries of the vocal tract and rest of the mesh was taken as courser mesh [45]. The size of the dense mesh along the wall boundaries of the vocal tract was adjusted by the parameter.
In the current work of the present thesis, we take another case for the formation of non- uniform mesh of the vocal tract. In the current approach, the dense mesh has been taken in the middle of the mesh while courser mesh has been implemented in the rest of the mesh. In each case of vowel, we find the minimum distance between the path of the vocal tract and 10-20% of this minimum distance is taken as central dense mesh of the vocal tract for different vowels. An example of the vowel / / ⊃ / can be seen in Figures 5-6.
In the above, two-dimensional non-uniform mesh has been designed to generate. Now numerical approach has been presented in the section. Figures of the vocal tract for each vowel is formed by the sequence of cross-sectional areas in the direction of length of vocal track. The shape of sequence of vowels / ⊃, / α /, /ξ /, /i / and / u / has taken from [41].
For the conversion of vocal track into the two-dimensional grid, the cross-sectional areas converted into the cylindrical tubes of different radii.
Now the shape of vocal track is represented with the help of above-mentioned technique that is a represented in the next figures. Reflection coefficient of glottis (rG), reflection coefficient of wall rw and reflection coefficient lip rL have assigned values 0.97, 1.0 and -0.9 respectively.
The resolution of the mesh in all demonstration has been chosen as 600. The length of the vocal tract for each case of the vowel is given in [46]. The unit sample length of the vowels / ⊃, / α /, /ξ /, /i / and / u / are 0.029, 0.028, 0.026, 0.029 and 0.03 cm respectively.
In the previous chapters, we have discussed the construction of two-dimensional non-uniform rectilinear grid and its process of implementation. We compare the response of the present model for non-uniform mesh with the response of the standard model with uniform mesh. In present thesis, we compare the current model with the standard model on bases of first six formant frequencies and frequency profiles. The first six formant frequencies are taken name as F1, F2, F3, F4, F5, F6 in the Table 1 and shown the results by the Figure 5. The efficiency and accuracy of the current model is matched with that of standard model in the form of collapsed time.
| Format frequency | Standard model | Non uniform model | Error (%) | Elapsed time | Efficiency (%) | |
|---|---|---|---|---|---|---|
| Standard model | Non uniform Model | |||||
| F1 | 634 | 610 | 3.8 | 491 | 357 | 37 |
| F2 | 1254 | 1280 | 2.1 | |||
| F3 | 2445 | 2438 | 0.3 | |||
| F4 | 3101 | 3179 | 2.5 | |||
| F5 | 4000 | 4052 | 1.3 | |||
| F6 | 5175 | 5170 | 0.09 | |||
Table 1 Numerical comparison of current model with the standard model for vowel.
Results and Discussions
For the Case of Vowel / ⊃ /
The shape of the vowel / ⊃ / with uniform mesh has been shown in Figure 5 while non-uniform mesh of the vowel /ɔ/ is presented in Figure 6. In this case, we have 17.46 as the length of the vocal tract and the sampling frequency is obtain as 1677 KHz. The frequency profiles of the standard model and the present model are compared in Figure 7 for vowel/c/. Figure 7 shows that the present model is very close to that of the standard model in the term of frequency profiles. The numerically calculated formants frequencies, errors and elapsed time is demonstrated in Table 1.
The percentage errors are given by the table are 3.8%, 2.1%, 0.3%, 2.5%, 1.3% with maximum error 3.8% at formant frequency F1 while the minimum relative error is 0.9% at formant frequency F6. Furthermore, this table illustrates that the current model is 37% more accurate than the standard model in the present case. This table demonstrates that the current model is very close to the standard model with the efficiency of 37%.
For the Case of Vowel /α /
Figures 8 and 9 demonstrate the meshing of the vocal tract for vowel /ɑ/ for uniform and non- uniform schemes of meshing respectively. The length of the vocal tract is also 17.46 cm with unit sample length of 0.029. The frequency responses of the two models are presented in Figure 10. We see that there is little difference between standard model with uniform mesh and the current model with non-uniform mesh. In other words, frequency profiles are very closed to each other.
Table 2 shows the numerically comparison between formant frequencies of standard model and the current model. Relative errors are given in the table are 5.9%, 1.2%, 0.8%, 0%, 0.5% and 0.04% where maximum relative error is 5.9% and minimum error is 0%. This table also illustrates that current model is 10% more efficient than the standard model in the case of the current vowel.
For the Case of Vowel /∈/
For the vowel of /∈/, the uniform and non-uniform meshing is presented by Figures 11 and 12. The smallest sample delay size in this current work has taken 0.026cm that result of sample rate 1843KHz. Figure 13 represents the frequency profiles of the both models. There is very good matching of the current model with that of standard model as depicted by Figure 13.
| Format frequency | Standard model | Non uniform model | Error (%) | Elapsed time | Efficiency (%) | |
|---|---|---|---|---|---|---|
| Standard model | Non uniform Model | |||||
| F1 | 680 | 640 | 5.9 | 602 | 547 | 10 |
| F2 | 1302 | 1317 | 1.2 | |||
| F3 | 2615 | 2593 | 0.8 | |||
| F4 | 3498 | 3498 | 0 | |||
| F5 | 4337 | 4315 | 0.5 | |||
| F6 | 5256 | 5254 | 0.04 | |||
Table 2 Numerical comparison of current model with the standard model for vowel.
Numerical computed format frequencies are given in Table 3. For the table, the relative maximum error between the standard and the present model is by 2.2% at formant frequency F2 and the minimum relative error is 0.06 at formant frequency F4. This leads to the closeness of the current model to the benchmark model. The present model is 19% more efficient then the standard model as shown by Table 3.
| Format frequency | Standardmodel | Non uniform model | Error(%) | Elapsed time | Efficiency(%) | |
|---|---|---|---|---|---|---|
| Standard model | Non uniform Model | |||||
| F1 | 610 | 615 | 0.8 | 630 | 529 | 19 |
| F2 | 1840 | 1800 | 2.2 | |||
| F3 | 2685 | 2695 | 0.4 | |||
| F4 | 3584 | 3582 | 0.06 | |||
| F5 | 4320 | 4380 | 1.4 | |||
| F6 | 5534 | 5542 | 0.1 | |||
Table 3 Numerical comparison of the current model with the standard model for vowel .
For the Case of Vowel / i /
Figures 14 and 15 illustrate the meshing of the vocal tract for vowel/i/ for uniform and non- uniform schemes of meshing respectively. Figure 16 shows the frequency profile of standard and the present model for vowel/i/. From the current figure, we conclude that the current model is comparable with that of standard model.
From Table 4, the relative errors of the current model with standard model are given as 6.1%, 3.5% 0.9%, 1.0%, 0.2%, and 0.2% respectively. The maximum relative error 6.1% is at formant frequency F1 while minimum relative error is 0.2% at formant frequencies F5 and F6. Finally Table 4 represent that the current model is 18% more efficient than the standard model.
| Format frequency | Standard model | Non uniform model | Error (%) | Elapsed time | Efficiency (%) | |
|---|---|---|---|---|---|---|
| Standard model | Non uniform Model | |||||
| F1 | 360 | 382 | 6.1 | 581 | 489 | 18 |
| F2 | 2000 | 1930 | 3.5 | |||
| F3 | 2973 | 2945 | 0.9 | |||
| F4 | 3645 | 3610 | 1.0 | |||
| F5 | 4599 | 4608 | 0.2 | |||
| F6 | 5690 | 5703 | 0.2 | |||
Table 4 Numerical comparison of the current model with the standard model for vowel /i/.
For the Case of Vowel / u /
For the vowel of / u /
For the vowel of / u /,the uniform and non-uniform meshing is depicted by Figures 17 and 18 respectively. Figure 19 shows the frequency profiles of the both models. There is very good matching of the current model with that of standard model as depicted by Figure 19.
Numerical computed format frequencies are mentioned in Table 5. For the table, the relative maximum error between the standard and the present model is by 4.1% and the minimum relative error is 0.1. This leads to the closeness of the current model to the benchmark model. The present model is 7% more efficient than the standard model as shown by Table 5.
| Format frequency | Standard model | Non uniform model | Error (%) | Elapsed time | Efficiency (%) | |
|---|---|---|---|---|---|---|
| Standard model | Non uniform Model | |||||
| F1 | 370 | 385 | 4.1 | 613 | 573 | 7 |
| F2 | 1530 | 1545 | 0.1 | |||
| F3 | 2105 | 2127 | 1.05 | |||
| F4 | 3338 | 3340 | 0.1 | |||
| F5 | 4265 | 4276 | 0.3 | |||
| F6 | 4990 | 4976 | 0.3 | |||
Table 5 Numerical comparison of the present model with the standard model for vowel /u/.
In the above figure (5) the doted frequency curve generated by the transfer function is a profile of current non uniform model and solid curves shows the profile of standard model that generated by the transfer function.
The peaks of the profile show the formant frequency of the model. The first column of table (1)shows the formant frequencies f1, f2, f3, f4, f5, f6, second and third column represent the standard model and non uniform model frequencies respectively.
Conclusion
In the current thesis, non-uniform mesh is used for modeling of vocal tract.
The dense mesh is taken in the middle of the vocal tract while course mesh is designed in the rest of the vocal tract. In the current approach, there are two types of delay lines in which large delay lines double the smaller delay lines which enables us to avoid the fractional delay for transfer function of non-uniform rectilinear grid. The simulation has been performed on the vowels /ɔ,
/ɑ/, /ɛ/, /i/ and /u/. By tables and figures, we draw following conclusions:
❖ Successful implementation of non-uniform rectilinear grid in the modeling of the vocal tract.
❖ Formant frequencies of the current model are very comparable to that of standard model of vocal tract.
❖ Frequency profiles of the present model are comparable to that of standard model.
The current model is more efficient than the standard model.
REFERENCES
- Podlubny I. Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Elsevier 1998; 27.
- Inan IE, Ugurlu Y, Bulut H. Auto-Bäcklund transformation for some nonlinear partial differential equation. Optik. 2016;127(22):10780-5.
- Wazwaz AM. Multiple-soliton solutions for the KP equation by Hirota’s bilinear method and by the tanh–coth method. Appl Math Comput 2007;190(1):633-40.
- Zayed EM, Alurrfi KA. A new Jacobi elliptic function expansion method for solving a nonlinear PDE describing the nonlinear low-pass electrical lines. Chaos Soliton Fract 2015;78:148-55.
- Naher H, Abdullah FA, Mohyud-Din ST. Extended generalized Riccati equation mapping method for the fifth-order Sawada-Kotera equation. AIP Advances 2013;3(5):052104.
- Sakar MG, Ergören H. Alternative variational iteration method for solving the time-fractional Fornberg–Whitham equation. Appl Math Model 2015;39(14):3972-9.
- Abdou MA, Soliman AA. New applications of variational iteration method. Physica D: Nonlinear Phenomena. 2005;211(1-2):1-8.
- Soliman AA. The modified extended direct algebraic method for solving nonlinear partial differential equations. Int J Sci 2008;6(2):136- 44
- Elwakil SA, El-Labany SK, Zahran MA, Sabry R. Modified extended tanh-function method for solving nonlinear partial differential equations. Physics Letters A 2002;299(2-3):179-88.
- Zhang S, Xia T. An improved generalized F-expansion method and its application to the (2+ 1) -dimensional KdV equations. Commun Nonlinear Sci Numer Simul 2008;13(7):1294-301.
- Navickas Z, Ragulskis M, Listopadskis N, Telksnys T. Comments on “Soliton solutions to fractional-order nonlinear differential equations based on the exp-function method”. Optik 2017; 223-231.
- Navickas Z, Telksnys T, Ragulskis M. Comments on “The exp-function method and generalized solitary solutions”. Comput Math with Appl 2015;69(8):798-803.
- Manafian J, Lakestani M. Application of tan (ϕ/2)-expansion method for solving the Biswas–Milovic equation for Kerr law nonlinearity. Optik 2016;127(4):2040-54.
- Akbulut A, Kaplan M, Tascan F. The investigation of exact solutions of nonlinear partial differential equations by using exp (−Φ (ξ)) method. Optik 2017;132:382-7.
- Li ZB, He JH. Fractional complex transform for fractional differential equations. Math Comput Appl 2010;15(5):970-3.
- Wen-An L, Hao C, Guo-Cai Z. The (ω/g)-expansion method and its application to Vakhnenko equation. Chinese Physics B 2009;18(2):400.
- Zhang Y. Solving STO and KD equations with modified Riemann– Liouville derivative using improved $(G’/G) $-expansion function method. IAENG Int J Appl Math 2015;45(1):16-22.
- Kilbas AA, Srivastava HM, Trujillo JJ. Theory and applications of fractional differential equations. Elsevier, UK. 2006.
- Kadem A, Kılıçman A. Note on transport equation and fractional Sumudu transform. Comput Math with Appl 2011;62(8):2995-3003.
- Gao GH, Sun ZZ, Zhang YN. A finite difference scheme for fractional sub-diffusion equations on an unbounded domain using artificial boundary conditions. J Comput Phys 2012;231(7):2865-79.
- Afzal I. Stationary Solutions and Optical Solitons for Nonlinear Schrodinger Equations (Doctoral dissertation, Department of Mathematics, COMSATS University Islamabad, Lahore campus).
- Ekici M, Mirzazadeh M, Sonmezoglu A, Ullah MZ, Asma M, Zhou Q, Moshokoa SP, Biswas A, Belic M. Dispersive optical solitons with Schrödinger–Hirota equation by extended trial equation method. Optik 2017;136:451-61.
- Naher H, Abdullah FA. Some New Traveling Wave Solutions of the Nonlinear Reaction Diffusion Equation by Using the Improved (��′/��)- Expansion Method. Math Probl Eng 2012.
- Bulut H, Sulaiman TA, Baskonus HM, Aktürk T. On the bright and singular optical solitons to the ($ $2+ 1$$2+ 1)-dimensional NLS and the Hirota equations. Opt Quantum Electron 2018;50(3):1-2.
- Zhang Y. Solving STO and KD equations with modified Riemann– Liouville derivative using improved $(G’/G) $-expansion function method. IAENG Int J Appl Math 2015;45(1):16-22.
- Kaur L, WazwazAM. Bright–dark optical solitons for Schrödinger- Hirota equation with variable coefficients. Optik 2019; 179:479-84.
- Yaşar E, Yıldırım Y, Zhou Q, Moshokoa SP, Ullah MZ, Triki H, Biswas A, Belic M. Perturbed dark and singular optical solitons in polarization preserving fibers by modified simple equation method. Superlattices Microstruct 2017;111:487-98.
- Zhou Q, Ekici M, Sonmezoglu A, Mirzazadeh M. Optical solitons with Biswas–Milovic equation by extended G′/G-expansion method. Optik 2016;127(16):6277-90.
- Zhou Q, Ekici M, Sonmezoglu A, Mirzazadeh M, Eslami M. Optical solitons with Biswas–Milovic equation by extended trial equation method. Nonlinear Dynamics. 2016;84(4):1883-900.
- Hassaballa AA, Elzaki TM. Applications of the improved G/G expansion method for solve Burgers-Fisher equation. J Comput Theor Nanosci 2017;14(10):4664-8.
- Khalil R, Al Horani M, Yousef A, Sababheh M. A new definition of fractional derivative. J Comput Appl Math 2014;264:65-70.
- Sulaiman TA, Bulut H, Baskonus HM. Optical solitons to the fractional perturbed NLSE in nano-fibers. Discrete Contin Dyn Syst - S. 2020;13(3):925.
- Ray SS. Dispersive optical solitons of time-fractional Schrödinger– Hirota equation in nonlinear optical fibers.Physica A: Statistical Mechanics and Its Applications.2020;537:122619.
- Sardar A, Ali K, Rizvi ST, Younis M, Zhou Q, Zerrad E, Biswas A, Bhrawy A. Dispersive optical solitons in nanofibers with Schrödinger- Hirota equation. J Nanoelectron Optoelectron 2016;11(3):382-7.
- Sardar A, Ali K, Rizvi ST, Younis M, Zhou Q, Zerrad E, Biswas A, Bhrawy A. Dispersive optical solitons in nanofibers with Schrödinger- Hirota equation. J Nanoelectron Optoelectron 2016;11(3):382-7.
- Mohamad-Jawad AJ. The Sine-Cosine Function Method for Exact Solutions of Nonlinear Partial Differential Equations. ARUC. 2013(32):124-43.
- Kilic B. Improved šG 0/GŽ-Expansion Method for the Time-Fractional Biological Population Model and Cahn–Hilliard Equation. J Comput Nonlinear Dyn 2015;10:051016-1.
- Zuo JM. Application of the extended G′ G-expansion method to solve the Pochhammer–Chree equations. Appl Math Comput 2010;217(1):376-83.
- Zuo JM. Application of the extended G′ G-expansion method to solve the Pochhammer–Chree equations. Appl Math Comput 2010 ;217(1):376-83.
- Jumarie G. Table of some basic fractional calculus formulae derived from a modified Riemann–Liouville derivative for non-differentiable functions. Appl Math Lett 2009;22(3):378-85.
- He JH, Li ZB. Converting fractional differential equations into partial differential equations. Thermal Sci 2012;16(2):331-4
- Bulut H, Sulaiman TA, Baskonus HM, Rezazadeh H, Eslami M, Mirzazadeh M. Optical solitons and other solutions to the conformable space–time fractional Fokas–Lenells equation. Optik 2018;172:20-7.
- Ismael HF, Bulut H, Baskonus HM. Optical soliton solutions to the Fokas–Lenells equation via sine-Gordon expansion method and $$(m+ ({G’}/{G})) $$(m+ (G′/G))-expansion method. Pramana 2020;94(1):1-9.
- Cattani C, Sulaiman TA, Baskonus HM, Bulut H. On the soliton solutions to the Nizhnik-Novikov-Veselov and the Drinfel’d-Sokolov systems. Opt Quantum Elec 2018;50(3):1-1.
- Gao W, Ghanbari B, Günerhan H, Baskonus HM. Some mixed trigonometric complex soliton solutions to the perturbed nonlinear Schrödinger equation. Mod Phys Lett B 2020;34(03):2050034.
- Zhu SD. The generalizing Riccati equation mapping method in non-linear evolution equation: application to (2+ 1)-dimensional Boiti– Leon–Pempinelle equation. Chaos Soliton Fract 2008;37(5):1335-42.

























