What is time?

Received: 09-Nov-2018 Accepted Date: Nov 12, 2018; Published: 19-Nov-2018

Citation: Kabe K. What is time? J Mod Appl Phys. 2018;2(2):25.

This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com

Introduction

The fundamental notion of time has dumbfounded intellectuals for millennia; even the usual human wondered at the motion of the heavens was inspired to keep time by virtue of the periodical nature of these heavens starting with the sun-rising from the east and setting in the west. Some civilizations had the lunar calendar. But what is the exact nature of time? Why does it confine all of matter, spacetime and in fact the whole of the universe to only one direction of dynamical evolution? Isaac Newton viewed time as something absolute and ever flowing. Relativity has changed our views of space and time. Our universe is now four dimensional in the classical limit. This, however, is not so in the quantum world. The classical world is a causal continuum determined by the causal structure knitted by the light cones defined at each event in the four dimensional spacetime continuum. Each event, a point in the spacetime, is due to all the events in the past light cone and this very same event is the cause of the entire future events in the future light cone. This holds for all events in the spacetime continuum. The conceptualization of time in the twentieth century, thus, was that of Einstein’s time. But what about time when we close in on the quantum domain? Weird effects dominate and time as such, calls a special attention. The quantum theory rests upon physical observables and the linear Hermitian operators associated with them. By this token even time is also a physical observable and should therefore have a linear Hermitian operators associated therein. But, it does not have one; the Pauli theorem asserts that. In fact, it is the basic problem in quantum gravity, since the Schrödinger equation for the quantum gravity has no time in it!

One can imagine states of quantum gravity as a fluid of light cones. Upon defining a vorticity for the system, one arrives at circulation for the system. It can be shown that analytical continuity between the eigenfunctions, which is a result from standard complex analysis, leads to a relation between time and circulation of the simple form.

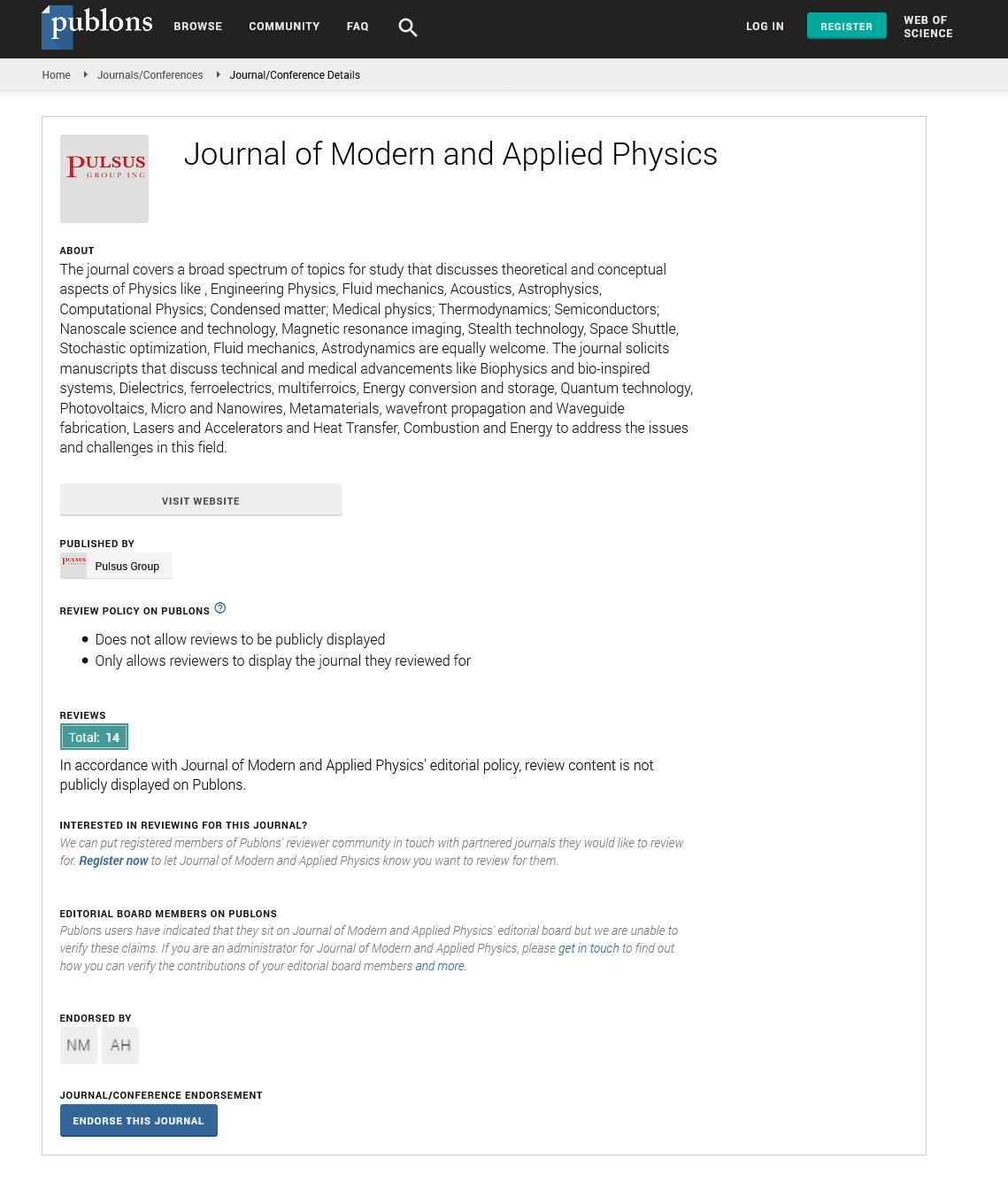
Thus to digress, the analytical continuity of the functions ψ (x) and ψ (Ï•) tells us that px corresponds to z J Ï• and similarly Et corresponds to mΓ so that we have by the Einstein theorem of inertia of energy that

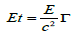
Thus time arises naturally as a kind of vorticity in the Hamiltonian quantum dynamics, although gravity doesn’t arise until curvature is involved; or

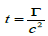
Now, for an inviscid liquid, with canonical time ϑ, the vorticity, 𝓌, satisfies the equation

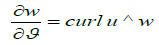
This equation tells us that inviscid fluids or quantum systems with zero viscosity do not have any vorticity. Thus, the equation 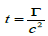, tells us that inviscid quantum systems are physically time independent, though we may clock them and the events involving them by attaching clocks to the respective frames of reference.

Universally speaking spacetime is viscous since it contains time (evolution). There are however, systems that may evolve independently of physical time which as we have seen before, appears in the problem of the Schrödinger equation for quantum gravity. This time, the vortex version, can be associated with the wavy nature of the quantum system. A similar consideration of the eigenfunction with the Boltzmann factor reveals a relationship between time and inverse temperature. Since, temperature arises due the average kinetic energy of the fundamental constituents of the system, this version of time is the particle version, thereby yielding the wave-particle duality in the nature of time-vortex time-inverse temperature time. Equivalence between time and circulation makes a headway in the understanding of time. The velocity of a dynamical system is related to the vorticity of the system. There follows what one might call the static gauge theory. This obeys the U(1) gauge invariance. Standard Anderson-Higgs mechanism yields a mass to the static gauge boson and consequently, time gets its asymmetry. This is the author’s current understanding of time.