Sign up for email alert when new content gets added: Sign up
Revisiting the problem of recovering functions in ℝn by integration on k Dimensional planes
The aim of this paper is to present inversion methods for the classical Radon transform which is defined on a family of k dimensional planes in â„Ân where 1≤k≤n–2. For these values of k the dimension of the set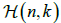 
, of all k dimensional planes in â„Ân, is greater than n and thus in order to obtain a well-posed problem one should choose proper subsets of 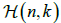. We present inversion methods for some prescribed subsets of 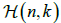which are of dimension n.
+447723598358
