Sum (2,M)-double fuzzifying continuity and characterizations of (2,M)-double fuzzifying topology
Received: 02-Apr-2018 Accepted Date: Apr 19, 2018; Published: 02-May-2018, DOI: 10.37532/2752-8081.18.2.6
Citation: Khalaf M. Sum (2,M)-Double fuzzifying continuity and Characteraizations of (2,M)-double fuzzifying topology. J Pur Appl Math. 2018;2(2):01-10.
This open-access article is distributed under the terms of the Creative Commons Attribution Non-Commercial License (CC BY-NC) (http://creativecommons.org/licenses/by-nc/4.0/), which permits reuse, distribution and reproduction of the article, provided that the original work is properly cited and the reuse is restricted to noncommercial purposes. For commercial reuse, contact reprints@pulsus.com
Abstract
(2,M)-double fuzzifying topology is a generalization of (2,M)- fuzzifying topology and classical topology. Motivated by the study of (2,M)- fuzzifying topology introduced by Höhle for fuzzifying topology. The main motivation behind this paper is introduce (2,M)-double fuzzifying topology as tight definition and a generalization of (2,M)- fuzzifying topology. Also, study structural properties of (2,M)-double fuzzifying continuous mapping, (2,M)- double fuzzifying quotient mapping, (2,M)-double fuzzifying operator, (2;M)- double fuzzifying totally continuous mapping and define an (2,M)-double fuzzifying Interior (closure) operator. The respective examples of these notions are investigated and the related properties are discussed. On the other hand, a characterization of (2,M)-fuzzifying topology by (2,M)-fuzzifying neighborhood system, where M is a completely distributive, was given in Höhle (2). We extended this defination and others to (2,M)-double fuzzifying topology. As an application of our results, we get characterizations of a (2,M)- double fuzzifying topology by these new notions. These characterizations do not exist in literature before this work. These concepts will help in verifying the existing characterizations and will be useful in achieving new and generalized results in future works.
Keywords
(2,M)-double fuzzifying topology; (2,M)-double fuzzifying continuous mapping; Characterizations of (2,M)-double fuzzifying topology
The uncertainty appeared in economics, engineering, environmental science, medical science and social sciences and so many other applied sciences is too complicated to be solved by traditional mathematical frameworks. The concept of (2,M)- fuzzifying topology appeared in Höhle [1,2] under the name “(2,M)-fuzzy topology” (cf. Definition 4.6, Proposition 4.11 in (2)) where L is a completely distributive complete lattice. In the case of L = [0,1] this terminology traces back to Ying [3-5] who studied the fuzzifying topology and elementarily developed fuzzy topology from a new direction with semantic method of continuous valued logic. Fuzzifying topology (resp. (2,M)-fuzzifying topology) in the sense of Ying (resp., Höhle) was introduced as a fuzzy subset (resp., an M-Fuzzy subset) of the power set of an ordinary set. (2,M)- fuzzifying topology is a kind of new mathematical model for dealing with uncertainty from a parameterization point of view. Also, Höhle’s in [2] from Theorems 1.4.2, 14.3, the concepts of (2,M)- fuzzifying topology and (2,M)- fuzzifying neighborhood system are equivalent notions. In my work we extended the notions of (2,M)- fuzzifying topology into (2,M)-double fuzzifying topology and studied the related properties and gave many valuable results for this theory which can be used as a generic mathematical tool for dealing with uncertainties. In the present paper, we apply the (2,M)-double fuzzifying topology, to M-double fuzzifying continuous mappings, M-double fuzzifying quotient mapping, (2,M)-double fuzzifying totally continuous mapping and define an (2,M)-double fuzzifying Interior (closure) operator. We extend and studied the notions of (2,M)-double fuzzifying neighborhood, M-double fuzzy contiguity relations, and M-double fuzzifying closure (interior) operator. Then our generalization of Höhle [2-5] results is obtained if we prove that M-double fuzzifying contiguity relation, (2,M)-double fuzzifying topology, (2,M)-double fuzzifying neighborhood system and M-double fuzzifying closure (interior) operator relation are equivalent notions. These characterizations do not exist in literature before this work. The basic properties of these notions are studied and characterizations of these concepts are discussed in detail. In Section 1.1, we introduce a survy about the definitions used in the article. In Section 1.2, we study structural properties of (2,M)-double fuzzifying continuous mapping, (2,M)- double fuzzifying quotient mapping, (2,M)-double fuzzifying operator.
In Section 1.3, we discuss (2,M)-double fuzzifying totally continuous and define an (2,M)-double fuzzifying Interior (closure) operator. The respective examples of these notions are investigated and the related properties are discussed. The basic properties of these notions are studied. On the other hand, in Section 1.4, a cheracterization of (2,M)-double fuzzifying topology by (2,M)-double fuzzifying neighborhood system, M-double fuzzifying contiguity relation, M-double fuzzifying interior operator are introduced, where M is a complete residuated lattice. For this paper M is complete residuated lattice and for more details see [6-12].
The following Definitions and Results introduced by Höhle [2].
Definition 1.1
The double negation law in a complete residuated lattice L is given as follows: L, (a→⊥)→⊥= a.
Definition 1.2
A structure (L,∨,∧,*,→,⊥,T) is called a strictly two-sided commutative quantale iff
(1) (L,∨,∧,⊥,T) is a complete lattice whose greatest and least element are ⊥,T respectively,
(2) (L,*,T) is a commutative monoid,
(3) (a)* is distributive over arbitrary joins, i.e.,
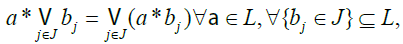
(b) → is a binary operation on L defined by:
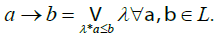
Definition 1.3
A structure (L,∨,∧,*,→,⊥,T) is called a complete MV- algebra iff the following conditions are satisfied:
1. (L,∨,∧,*,→,⊥,T) is a strictly two-sided commutative quantale,
2. ∀a, b∈L, (a→b)→b = a ∨ b.
Definition 1.4
Let x∈ X. The fuzzifying neighbourhood system of x , denoted by 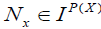 , is defined as follows:
, is defined as follows: 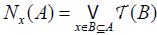 .
.
Definition 1.5
Let X be a nonempy set. An element c∈LX ×P( X ) is called an M-fuzzy contiguity relation on X iff c fulfills the following axioms:
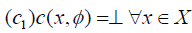 .
.
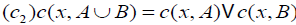 , (Distributivity),
, (Distributivity),
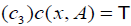 , whenever x∈ A,
, whenever x∈ A,
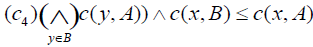 . (Transitivity).
. (Transitivity).
Theorem 1.1
Let 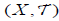 be an (2,M)-fuzzifying topological space, and let L satisfies the completely distributive law then the (2,M)-fuzzifying neighborhood system
be an (2,M)-fuzzifying topological space, and let L satisfies the completely distributive law then the (2,M)-fuzzifying neighborhood system 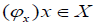 satisfies the following conditions:
satisfies the following conditions:
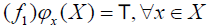 , (Boundary conditions)
, (Boundary conditions)
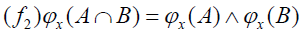 , (Intersection property)
, (Intersection property)
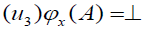 whenever x∉ A
whenever x∉ A
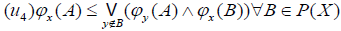 . Furthermore
. Furthermore
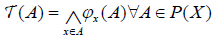 .
.
Theorem 1.2
Let L satisfies the completely distributive law and Let 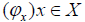 be a system satisfies the properties
be a system satisfies the properties 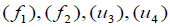 in Theorem 1.4.2 above. Then
in Theorem 1.4.2 above. Then 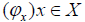 induces an (2,M)-fuzzifying topology
induces an (2,M)-fuzzifying topology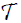 on X by
on X by 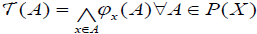 . Moreover the following formula holds
. Moreover the following formula holds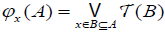 .
.
Theorem 1.3
Let (L,≤,*) be a complete MV-algebra and ☉ = ∧. further more let (L,≤) be a completely distributive lattice complete MV -algebra. Then (2,M)-fuzzifying topologies, M-fuzzy contiguity relations and stratified and transitive M-topologies are equivalent concepts.
Definition 1.6
Let X be a nonempty set. A map ()° : 2X → LX is called an M-fuzzifying interior operator if ()° satisfies the following conditions:
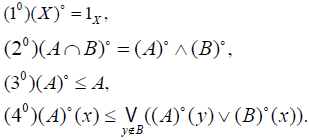
Definition 1.7
[1] Let X be a nonempty set and let P(X) be the family of all ordinary subsets of X. An element T ∈MP(X) is called an M-fuzzifying topology on X iff it satisfies the following axioms:
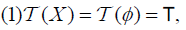
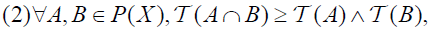
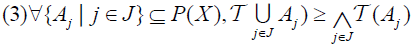 . The pair (X, T) is called an M-fuzzifying topological space.
. The pair (X, T) is called an M-fuzzifying topological space.
Definition 1.8
(2.13). A structure (L,∨,∧,*,→,⊥,T) is called a complete residuated lattice if f
(1) (L,∨,∧,⊥,T) is a complete lattice whose greatest and least element are ⊥,T respectively,
(2) (L,*,T) is a commutative monoid, i.e.,
(a) * is a commutative and associative binary operation on L, and (b) ∀a,∈L,a *T = T*a = a,
(3)(a) * is isotone,
(b) → is a binary operation on L which is antitone in the …first and isotone in the second variable,
(c) →is couple with * as: a *b ≤ c iff a ≤ b→c ∀a,b,c∈L
2. (2,M)-Double fuzzifying Continuous mapping.
Definition 2.1
Let X be a nonempty set. The pair 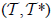 of maps
of maps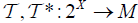 is called an (2,M)-double fuzzifying topology on X if it satisfies the following conditions:
is called an (2,M)-double fuzzifying topology on X if it satisfies the following conditions:
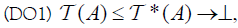 for each A∈2X,
for each A∈2X,
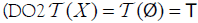 and
and 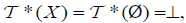
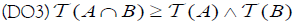 and
and
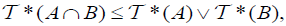 for each A, B∈2X.
for each A, B∈2X.
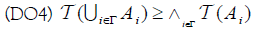 and
and 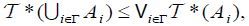 for each
for each .
.
The pair  is called an (2,M)-double fuzzifying topological space. And
is called an (2,M)-double fuzzifying topological space. And 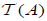 and
and 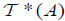 may be explained as a gradation of openness and gradation of nonopenness for A.
may be explained as a gradation of openness and gradation of nonopenness for A.
Remark 2.1
Let 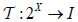 be fuzzifying topology on X. Define a map
be fuzzifying topology on X. Define a map 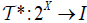 by
by 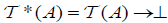 . Then when M = I , ☉ = ∧ and
. Then when M = I , ☉ = ∧ and 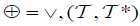 is an (2,M)-double fuzzifying topology on X. Therefore, (2,M)-double fuzzifying topology is a generalization of fuzzifying topology due to [13,14] and [15].
is an (2,M)-double fuzzifying topology on X. Therefore, (2,M)-double fuzzifying topology is a generalization of fuzzifying topology due to [13,14] and [15].
Definition 2.2
Let 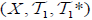 and
and 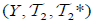 be two (2,M)-double fuzzifying topological spaces and for each B∈2Y. Then, The map
be two (2,M)-double fuzzifying topological spaces and for each B∈2Y. Then, The map 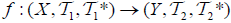 is called an M-double fuzzifying continuous map, if
is called an M-double fuzzifying continuous map, if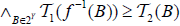 and
and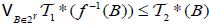 .
.
Example 2.1
Let X = Y = {a,b}, L = [0,1] and if 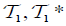 and
and 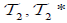 defined as follows:
defined as follows:
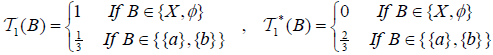 and
and
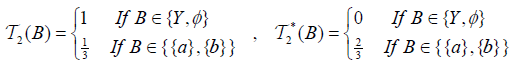 The pairs
The pairs 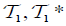 and
and 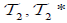 is called an (2,M)-double fuzzifying topological spaces on X. The map
is called an (2,M)-double fuzzifying topological spaces on X. The map 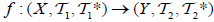 define by f (a) = b and f (b) = a is an M-double fuzzifying continuous map.
define by f (a) = b and f (b) = a is an M-double fuzzifying continuous map.
Theorem 2.1
Let 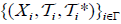 be a family of an (2,M)-double fuzzifying topological space. And let Y be a set, let
be a family of an (2,M)-double fuzzifying topological space. And let Y be a set, let 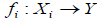 be a mapping for each i∈Γ. Define a map
be a mapping for each i∈Γ. Define a map 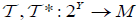 by
by 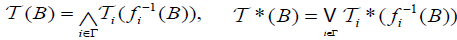 . For all B∈2Y.Then:
. For all B∈2Y.Then:
(1) 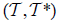 is an (2,M)-double fuzzifying topological space on Y for which each fi is an M-double fuzzifying continuous mapping.
is an (2,M)-double fuzzifying topological space on Y for which each fi is an M-double fuzzifying continuous mapping.
(2) 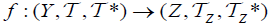 is an M-double fuzzifying continuous map iff each
is an M-double fuzzifying continuous map iff each 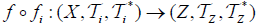 is an M-double fuzzifying continuous map.
is an M-double fuzzifying continuous map.
Proof
(1) From the definition of 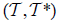 easily get (DO1) and (DO2) are trivial. (DO3)
easily get (DO1) and (DO2) are trivial. (DO3)
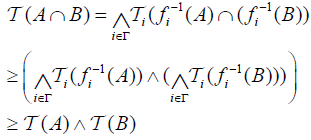
and
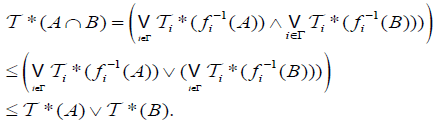
(DO4) For any family 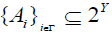
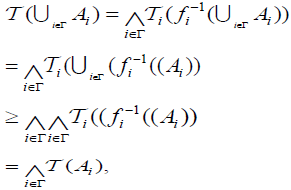
and
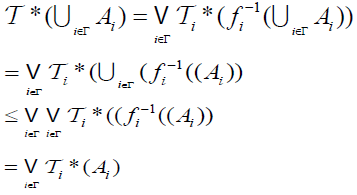
(2) (⇐) Since 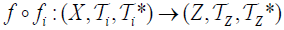 is an M-double fuzzifying continuous, we have for each
is an M-double fuzzifying continuous, we have for each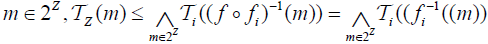 . an
. an 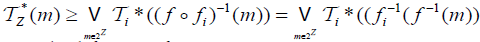 . From the defination of
. From the defination of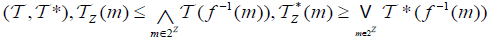 . For all B∈2Z. Hence
. For all B∈2Z. Hence 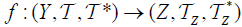 is an M-double fuzzifying continuous map.
is an M-double fuzzifying continuous map.
(⇒) simple.
Definiation 2.3
Let 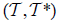 be defined as in Theorem 2.1. Then the frame
be defined as in Theorem 2.1. Then the frame 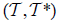 is called final (2,M)-double fuzzifying topology on Y associated with the families
is called final (2,M)-double fuzzifying topology on Y associated with the families 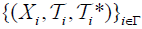 and
and 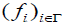 .
.
Corollary 2.1
Let 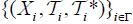 be a family of (2,M)-double fuzzifying topological spaces, for (i ≠ j)∈Γand
be a family of (2,M)-double fuzzifying topological spaces, for (i ≠ j)∈Γand 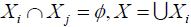 . Let : idi Xi → X be identity map for which i∈Γ.
. Let : idi Xi → X be identity map for which i∈Γ.
Define the map 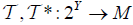 by
by 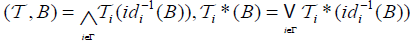 . For all B∈2Y Then:
. For all B∈2Y Then:
(1) 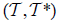 be an (2,M)-double fuzzifying topological space on X for each idi is an M-double fuzzifying continuous map.
be an (2,M)-double fuzzifying topological space on X for each idi is an M-double fuzzifying continuous map.
(2) 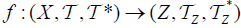 is an M-double fuzzifying continuous map iff each
is an M-double fuzzifying continuous map iff each 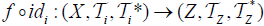 is an M-double fuzzifying continuous map.
is an M-double fuzzifying continuous map.
Corollary 2.2
Let Y be a set and 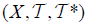 be an (2,M)-double fuzzifying topological space, let f : X →Y be a surjective mapping. Define mappings
be an (2,M)-double fuzzifying topological space, let f : X →Y be a surjective mapping. Define mappings 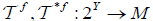 By
By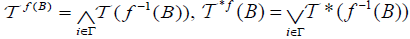 for all B∈2Y. Then:
for all B∈2Y. Then:
(1) 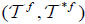 is an (2,M)-double fuzzifying topological space on X which f is an M-double fuzzifying continuous map.
is an (2,M)-double fuzzifying topological space on X which f is an M-double fuzzifying continuous map.
(2) 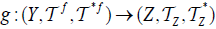 is an M-double fuzzifying continuous map iff each
is an M-double fuzzifying continuous map iff each 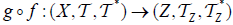 is an M-double fuzzifying continuous map.
is an M-double fuzzifying continuous map.
Definiation 2.4
Let 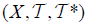 be an (2,M)-double fuzzifying topological space. And Y a set, let f : X →Y be a surjective mapping. The (2;M)-double fuzzifying topological space
be an (2,M)-double fuzzifying topological space. And Y a set, let f : X →Y be a surjective mapping. The (2;M)-double fuzzifying topological space 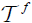 on Y associated the
on Y associated the 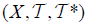 and f is called the quotient (2;M)-double fuzzifying topological space and the map is called M-double fuzzifying quotient map.
and f is called the quotient (2;M)-double fuzzifying topological space and the map is called M-double fuzzifying quotient map.
Definition 2.5
Let 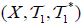 and
and 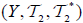 be two (2,M)-double fuzzifying topological spaces and for each B∈2Y.Then,
be two (2,M)-double fuzzifying topological spaces and for each B∈2Y.Then,
(i) The map 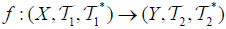 is called an M-double fuzzifying openess, if
is called an M-double fuzzifying openess, if 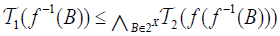 and
and 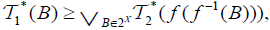
(ii) The map 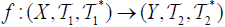 is called an M-double fuzzifying closness if
is called an M-double fuzzifying closness if 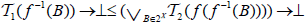 and
and 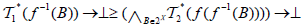 .
.
Theorem 2.2
Let 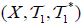 and
and 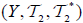 be two (2,M)-double fuzzifying topological spaces, let
be two (2,M)-double fuzzifying topological spaces, let 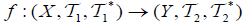 be a surjective an M-double fuzzifying continuous mapping. Then (1) If
be a surjective an M-double fuzzifying continuous mapping. Then (1) If 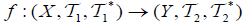 is an M-double fuzzifying openess, then f is M-double fuzzifying quotient map.
is an M-double fuzzifying openess, then f is M-double fuzzifying quotient map.
(2) 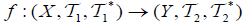 is an M-double fuzzifying closness, then f is M-double fuzzifying quotient map.
is an M-double fuzzifying closness, then f is M-double fuzzifying quotient map.
Proof
(1) Only, should prove that 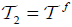 . So, From Corollary 2.2 and Definition 2.5 we have,
. So, From Corollary 2.2 and Definition 2.5 we have,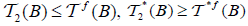 for all B∈2Y Conversely, we have
for all B∈2Y Conversely, we have
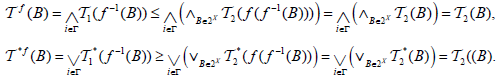
(3) Trivial.
Theorem 2.3.
A map 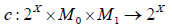 is called an M- fuzzifying closure operator if for each A, B∈2X , r∈L0, s∈L1 with r ≤ s→⊥. The operator c satisfies the following conditions:
is called an M- fuzzifying closure operator if for each A, B∈2X , r∈L0, s∈L1 with r ≤ s→⊥. The operator c satisfies the following conditions:
c(1) c(φ , r, s) =φ ,
c(2) A ⊆ c(A, r, s),
c(3) If A ⊆ B,then c(A, r, s) ⊆ c(B, r, s),
c(4) If 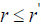 and
and 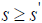 with
with 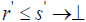 then
then 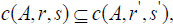
c(5) 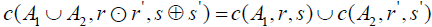 , Then
, Then
the pair (X ,c) is an M- fuzzifying closure space. An M- fuzzifying closure space (X ,c) is called topological if
c(6) c(c(A, r, s)) = c(A, r, s) for each A, B∈2X , r∈L0, s∈M1 with r ≤ s→⊥ .
Definiation 2.6
Let (X ,c1) and (Y,c2) be two M-fuzzifying closure spaces. A map f : (X ,c1)→(Y,c2) is said to be a c -map if for all A∈2X, r ∈ M1, s ∈ M2 with r →s ⊥, f (c1 (A, r, s)) ≤ c2 ( f (A), r, s)).
Theorem 2.4
Let Y be a set and let 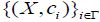 be a collection of an M-fuzzifying closure spaces, let :ii f X →Y be a surjective mapping for each i∈Γ. Define a mappings
be a collection of an M-fuzzifying closure spaces, let :ii f X →Y be a surjective mapping for each i∈Γ. Define a mappings
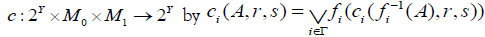 .
.
Then:
(1) c is an M- fuzzifying space on Y for each fi is c -map,
(2) 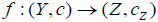 is C-map iff each
is C-map iff each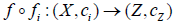 is c -map.
is c -map.
Proof
(1) c(1),c(3),c(4) and c(5) come directly from the definition of c. For c(2), we have,
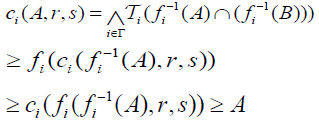
Hence 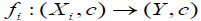 is c -map.
is c -map.
(2) (⇒) simple.
(⇐) Let 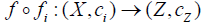 be a c -map, we have
be a c -map, we have
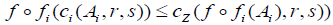
It implies
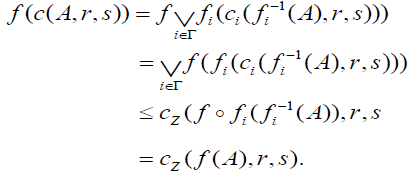
From Theorem 2.4 we introduce the following definition
Definiation 2.7
The structure c is called an M- fuzzifying operator on Y associated with the families 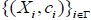 and
and 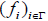 .
.
Corollary 2.3
Let 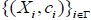 be a family of an M- fuzzifying operator, for (i ≠ j)∈Γand
be a family of an M- fuzzifying operator, for (i ≠ j)∈Γand 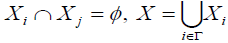 . Let
. Let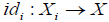 be identity map for which i∈Γ.
be identity map for which i∈Γ.
Define the map 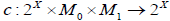 by
by
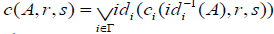 .
.
Then:
(1) c is an M- fuzzifying operator on X for which idi is c -map,
(2) 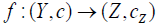 is c -map iff each
is c -map iff each 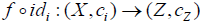 is c -map.
is c -map.
Definiation 2.8
Let (X ,c) be an M- fuzzifying operator. And Y a set, let f : X →Y be a surjective map. Define the map 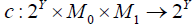 by
by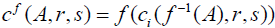 . Then (Y,c f ) induced by f is called an M- fuzzifying quotient space of (X ,c) and the function f is called an an M-fuzzifying quotient map.
. Then (Y,c f ) induced by f is called an M- fuzzifying quotient space of (X ,c) and the function f is called an an M-fuzzifying quotient map.
Theorem 2.5
Let Y be a set and 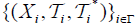 be a collection of an (2,M)- fuzzifying topological spaces, let
be a collection of an (2,M)- fuzzifying topological spaces, let 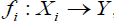 , be a surjective map for each i∈Γ and
, be a surjective map for each i∈Γ and 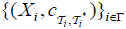 a collection of an M- fuzzifying operator induced by
a collection of an M- fuzzifying operator induced by 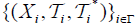 . Define the functions
. Define the functions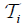 and
and 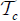 on Y by
on Y by 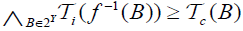 and
and 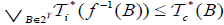 and the map
and the map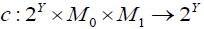 by
by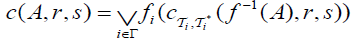 . Then
. Then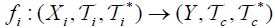 an M- fuzzifying continuous mapping.
an M- fuzzifying continuous mapping.
Proof
Suppose there exists B∈2Y such that 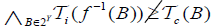 and
and 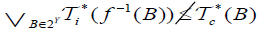 then there exists
then there exists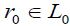 ,
, 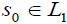 with
with 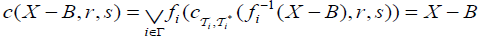 such that
such that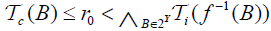 and
and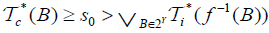 .
.
On the other hand, we have
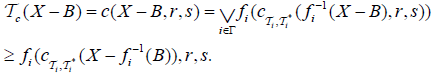
It implies
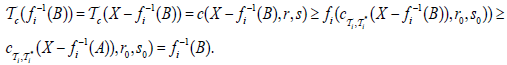 Then
Then
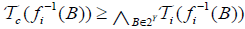 and by the same ways
and by the same ways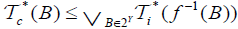 , we have
, we have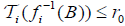 and
and 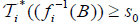 , which a contradiction.
, which a contradiction.
Hence 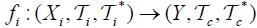 an M-double fuzzifying continuous mapping.
an M-double fuzzifying continuous mapping.
3. Totally Continuous in (2;M)-double fuzzifying topological spaces.
Definition 3.1
Let 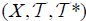 be an (2,M)-double fuzzifying topological space. Define an (2,M)-double fuzzifying Interior operator
be an (2,M)-double fuzzifying topological space. Define an (2,M)-double fuzzifying Interior operator 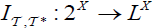 by:
by:
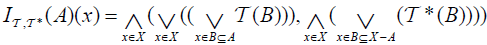 .
.
Definition 3.2
Let 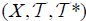 be an (2,M)-double fuzzifying topological space. Define an (2,M)-double fuzzifying closure operator
be an (2,M)-double fuzzifying topological space. Define an (2,M)-double fuzzifying closure operator 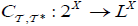 by:
by:
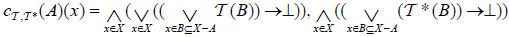 .
.
Example 3.1
Let X = {a,b,c}, L = [0,1] and. Let 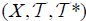 be an (2,M)-double fuzzifying topological space defined by
be an (2,M)-double fuzzifying topological space defined by
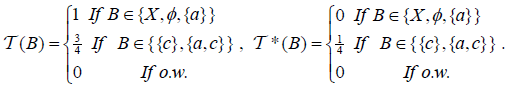
If A = {a,b}. Then 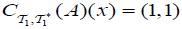 and
and 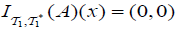 .
.
Definition 3.3
Let 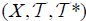 be an (2,M)-double fuzzifying topological space. Let
be an (2,M)-double fuzzifying topological space. Let 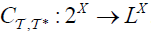 . If its extension
. If its extension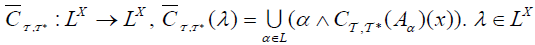 .
.
Where 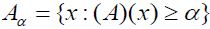 satisfies the following statments:
satisfies the following statments:
(1) 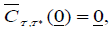
(2) 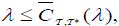
(3) 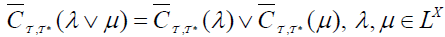
(4) 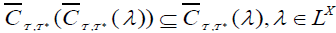 .
.
Definition 3.4
Let 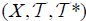 be an (2,M)-double fuzzifying topological space and A ⊆ X.
be an (2,M)-double fuzzifying topological space and A ⊆ X.
(i) An M-double fuzzifying 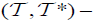 semi open set (briefly,
semi open set (briefly, 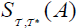 ) of A, defined as follows:
) of A, defined as follows:
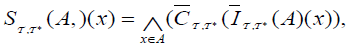
(ii) An M-double fuzzifying 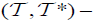 semi closed set ( briefly,
semi closed set ( briefly, 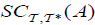 ) of A, if
) of A, if 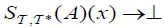 is An M-double fuzzifying
is An M-double fuzzifying 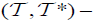 semi open,
semi open,
(iii) (iii) AnM-double fuzzifying 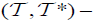 semi clopen set ( briefly,
semi clopen set ( briefly, 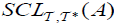 ) of A, if A has
) of A, if A has 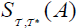 and
and 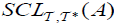 .
.
(iv) An M-double fuzzifying 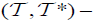 pre open set (briefly,
pre open set (briefly,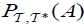 ) of A, defined as follows:
) of A, defined as follows:
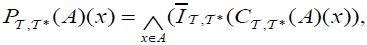
(v) An M-double fuzzifying 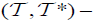 pre closed set (briefly,
pre closed set (briefly,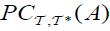 of A, if
of A, if 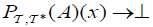 is An M-double fuzzifying
is An M-double fuzzifying 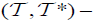 pre open.
pre open.
(vi) AnM-double fuzzifying 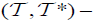 pre clopen set (briefly,
pre clopen set (briefly, 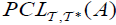 ) of A, if A has
) of A, if A has 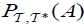 and
and 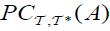 .
.
Remark 3.1
An M-double fuzzifying 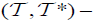 clopen set (briefly,
clopen set (briefly, 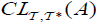 ) of A, if and only if A has
) of A, if and only if A has 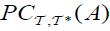 and
and 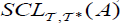 .
.
Example 3.2
In Example 3.1 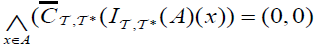 .
.
Definition 3.5
Let 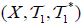 and
and 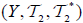 be two (2,M)-double fuzzifying topological spaces.
be two (2,M)-double fuzzifying topological spaces.
Then,
(i) The map 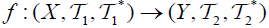 is called an M-double fuzzifying totally continuous (briefly, dftc), if for each B∈2Y have
is called an M-double fuzzifying totally continuous (briefly, dftc), if for each B∈2Y have
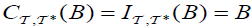 , then,
, then,
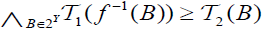 and
and 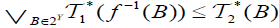 .
.
(ii) The 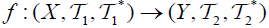 is called an M-double fuzzifying semi continuous ( briefly, df sc), if for each
is called an M-double fuzzifying semi continuous ( briefly, df sc), if for each 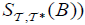 of B∈2Y,
of B∈2Y, 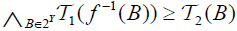 and
and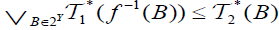 .
.
(iii) The map 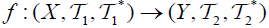 is called an M-double fuzzifying totally semicontinuous (briefly, dftsc), if for each
is called an M-double fuzzifying totally semicontinuous (briefly, dftsc), if for each 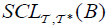 of B∈ 2Y,
of B∈ 2Y, 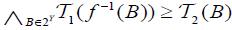 and
and 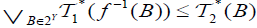 .
.
(iv) The map 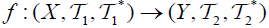 is called an M-double fuzzifying totally precontinuous (briefly, dftpc), if for each
is called an M-double fuzzifying totally precontinuous (briefly, dftpc), if for each 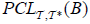 of B∈2Y ,
of B∈2Y , 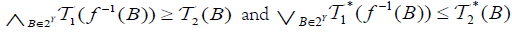 .
.
Definition 3.6
Let 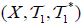 and
and 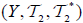 be two (2;M)-double fuzzifying topological spaces and for each B∈2Y.Then,
be two (2;M)-double fuzzifying topological spaces and for each B∈2Y.Then,
(i) The map 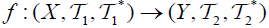 is called an M-double fuzzifying openess, if
is called an M-double fuzzifying openess, if 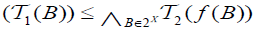 and
and 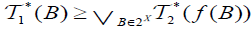 ,
,
(ii) The map 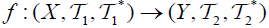 is called an M-double fuzzifying closness,
is called an M-double fuzzifying closness, 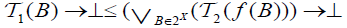 and
and 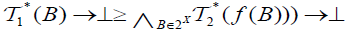 .
.
Theorem 3.1
Let 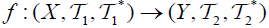 be a mapping. Then the following are equivalent:
be a mapping. Then the following are equivalent:
(i) f is a dftc mapping,
(ii) 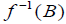 is an
is an 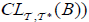 of B. such that
of B. such that  and
and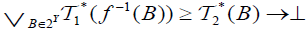 for each B∈2Y,
for each B∈2Y,
(iii) 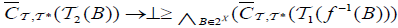 and
and 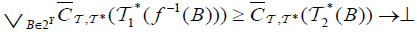 for each B∈2Y,
for each B∈2Y,
(iv)  and
and 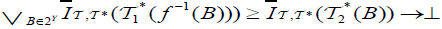 for each B∈2Y.
for each B∈2Y.
Proof
Follow directly from Definition 3.3 and Definition 3.5
Definition 3.6
Let 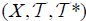 be an (2,M)-double fuzzifying topological space and A ⊆ X.
be an (2,M)-double fuzzifying topological space and A ⊆ X.
(i) An M-double fuzzifying 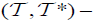 generalized closed set
generalized closed set 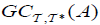 of A, defined as follows:
of A, defined as follows:
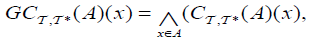
(ii) An M-double fuzzifying 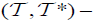 generalized open set
generalized open set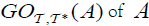 if
if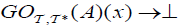 is an M-double fuzzifying
is an M-double fuzzifying 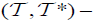 generalized closed.
generalized closed.
Definition 7.7
Let 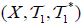 and
and 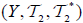 be two (2,M)-double fuzzifying topological spaces. Then,
be two (2,M)-double fuzzifying topological spaces. Then,
(i) The map 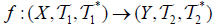 is called double fuzzifying irresolute if, An M-double fuzzifying
is called double fuzzifying irresolute if, An M-double fuzzifying 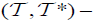 semi open set of
semi open set of 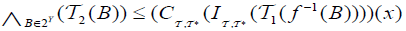 and
and 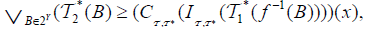
(ii) The map 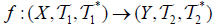 is called double fuzzifying pre semi close, if
is called double fuzzifying pre semi close, if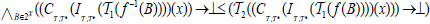 and
and 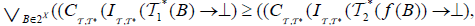
Definition 3.8 Let 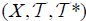 be an (2,M)-double fuzzifying topological space and A ⊆ X.
be an (2,M)-double fuzzifying topological space and A ⊆ X.
(i) An M-double fuzzifying 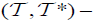 semi generalized closed set
semi generalized closed set 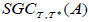 of A, defined as follows:
of A, defined as follows:
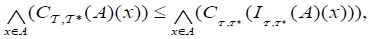
(ii) An M-double fuzzifying  semi generalized open set
semi generalized open set of A, if
of A, if 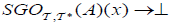 is an M-double fuzzifying
is an M-double fuzzifying 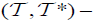 semi generalized closed,
semi generalized closed,
Theorem 2.1
Let 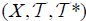 be an (2,M)-double fuzzifying topological space.
be an (2,M)-double fuzzifying topological space.
(1) Let A ⊆ X, A has an 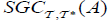 then B has an
then B has an 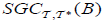 .
.
(2) If A has an 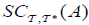 , then it has
, then it has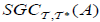 .
.
Proof
Follow directly from Definition 3.3 and Definition 3.8
Remark 3.1
The converse of (2) in Theorem 2.1 is not true in general.
Remark 3.2
Let 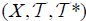 be an (2,M)-double fuzzifying topological space. Let A ⊆ B, then the concepts of
be an (2,M)-double fuzzifying topological space. Let A ⊆ B, then the concepts of 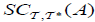 , and
, and 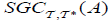 are independent concepts.
are independent concepts.
Theorem 3.2
Let 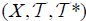 be an (2,M)-double fuzzifying topological space. Define the an operator semi generalized M-double fuzzifying closure operator
be an (2,M)-double fuzzifying topological space. Define the an operator semi generalized M-double fuzzifying closure operator 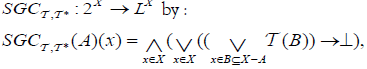
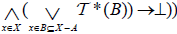 . Such that B has an
. Such that B has an 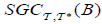 , the operator
, the operator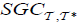 , satisfies the following statments: (1)
, satisfies the following statments: (1) 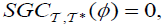
(2) 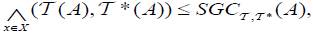
(3) 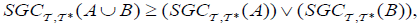
(4) 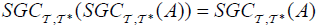
(5) If A has an 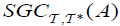 then it has
then it has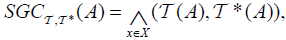
(6) 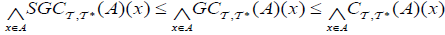 .
.
Proof
Follow directly from Definition 3.3 and Definition 3.8
Theorem 3.3
Let 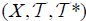 be an (2,M)-double fuzzifying topological space. Define the an operator semi generalized M-double fuzzifying interior operator
be an (2,M)-double fuzzifying topological space. Define the an operator semi generalized M-double fuzzifying interior operator 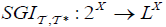 by:
by:
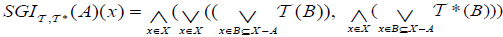 .
.
Such that B has an 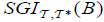 . The operator
. The operator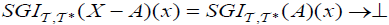 .
.
Theorem 2.4
Let 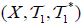 and
and 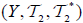 be two (2,M)-double fuzzifying topological spaces. Then the map
be two (2,M)-double fuzzifying topological spaces. Then the map 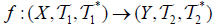 is called
is called
(i) df ap − irresolute if f −1(B) has an 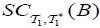 for each B ⊆Y has an
for each B ⊆Y has an 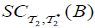 ,
,
(ii) df ap − semi closed if f (A) has an 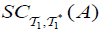 for each A ⊆Y has an
for each A ⊆Y has an 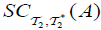 .
.
Definition 3.10
Let 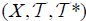 be an (2,M)-double fuzzifying topological space. A set A is called double fuzzifying semi clopen (for short, df clo − set), if it has an
be an (2,M)-double fuzzifying topological space. A set A is called double fuzzifying semi clopen (for short, df clo − set), if it has an 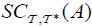 and
and 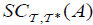 for each A ⊆ X.
for each A ⊆ X.
4. Characteraizations of (2,M)-double fuzzifying topology
In this section M is assumed to be a completely distributive complete residuated lattice, where M satisfies the double negation law. In (Corollary 2.15 (Höhle) (2)) proved that the M-fuzzy contiguity relations and (2,M)- fuzzifying topologies are equivalent notions if L is a completely distributive complete MV-algebra. In the following we prove that M-double-fuzzy contiguity relations and (2,M)-double-fuzzifying topology are equivalent notions just if L is a completely distributive complete residuated lattice satisfies the double negation law so that we give a generalization of U. Höhle’s result. In (Höhle (2)) the concepts of (2,M)- fuzzifying topology and (2,M)- fuzzifying neighborhood system are equivalent notions. Then our generalization of U.Höhle’s result is obtained if we prove that,
(1) (2,M)-double fuzzifying topology and (2,M)- double fuzzifying neighborhood system,
(2) M-double fuzzifying contiguity relation and (2,M)-double fuzzifying neighborhood system,
(3) M-double fuzzifying interior operator and (2,M)-double fuzzifying neighborhood system are equivalent notions.
Definition 4.1
Let X be a nonempty set and x∈ X. If L satisfies a completely distributive law. Then the pair 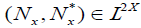 is called an (2,M)-double fuzzifying neighborhood system of x if satisfies the following conditions:
is called an (2,M)-double fuzzifying neighborhood system of x if satisfies the following conditions:
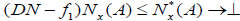 , for each. A∈ 2X And
, for each. A∈ 2X And 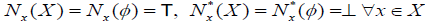 , (Boundary conditions)
, (Boundary conditions)
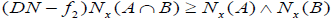 , and
, and 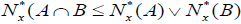 for each A, B∈2X (Intersection property)
for each A, B∈2X (Intersection property)
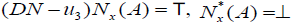 whenever
whenever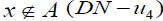 For each x∈ A, ∀B∈P(X ),
For each x∈ A, ∀B∈P(X ),
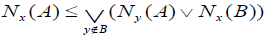 and
and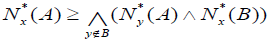 .
.
Theorem 4.1
Let the pair 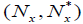 be an (2,M)-double fuzzifying neighborhood system. And
be an (2,M)-double fuzzifying neighborhood system. And 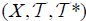 be an (2, L) − double fuzzifying topological space. We define the maps
be an (2, L) − double fuzzifying topological space. We define the maps 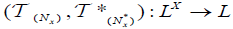 as follows:
as follows:
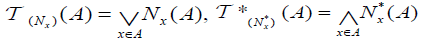
Then the pair 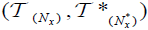 is an (2, L) -double fuzzifying topological space induces by (2,M)-double fuzzifying neighborhood system
is an (2, L) -double fuzzifying topological space induces by (2,M)-double fuzzifying neighborhood system 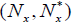 .
.
Let 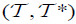 be an (2, L) − double fuzzifying topological space. We define the maps
be an (2, L) − double fuzzifying topological space. We define the maps 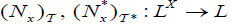 as follows:
as follows:
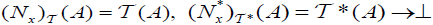
Then 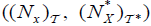 is an an (2,M)-double fuzzifying neighborhood system induces by an (2, L) -double fuzzifying topological space on X. Furthermore
is an an (2,M)-double fuzzifying neighborhood system induces by an (2, L) -double fuzzifying topological space on X. Furthermore 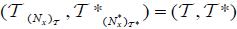 .
.
Proof
(A) (DO1) For each A∈LX,
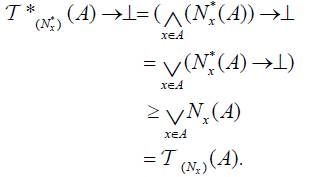
(DO2) 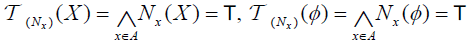 and
and 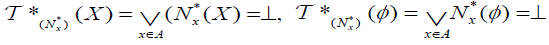 (DO3) for each A, B∈2X,
(DO3) for each A, B∈2X,
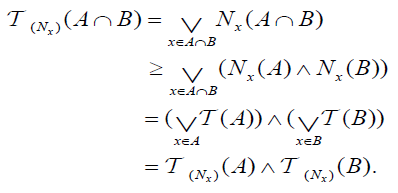
and
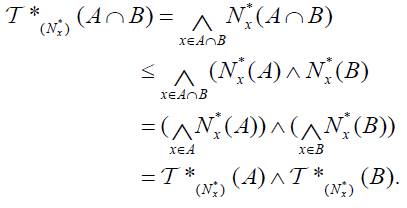 (DO4) For each
(DO4) For each
 .
.
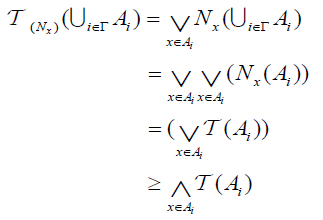
and
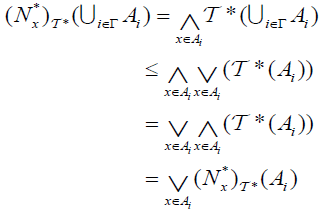
(B) 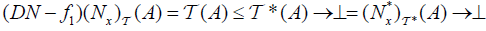 ,
, 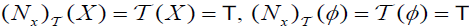 and
and 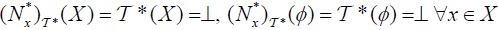 , (Boundary conditions)
, (Boundary conditions)
(DN − f2) For each A, B∈2X (Intersection property)
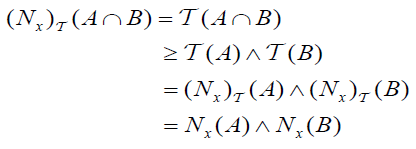
and
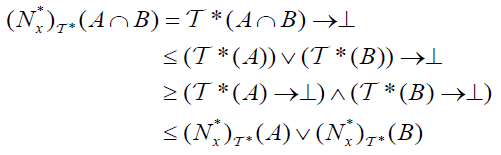
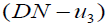 whenever x∉ A,
whenever x∉ A, 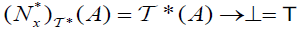 and
and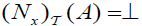 .
.
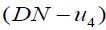 Let
Let 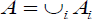
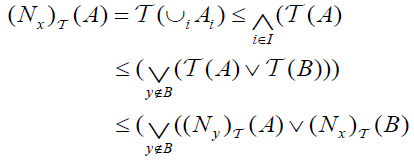
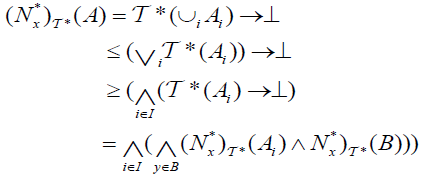
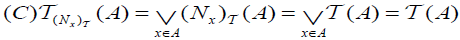 and
and 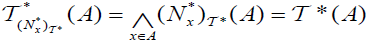 .
.
Definition 4.2
Let X be a nonempy set. An element 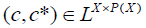 is called an M-double fuzzy contiguity relation on X iff C fulfills the following axioms:
is called an M-double fuzzy contiguity relation on X iff C fulfills the following axioms:
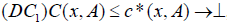 , for every x∈ X and A∈2X.
, for every x∈ X and A∈2X.
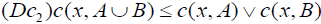 , and
, and
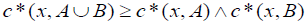 (Distributivity),
(Distributivity),
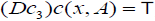 , and c*(x, A) =⊥ whenever x∈ A,
, and c*(x, A) =⊥ whenever x∈ A,
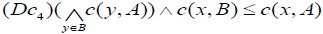 and
and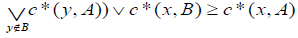 (Transitivity).
(Transitivity).
Theorem 4.2
Let 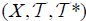 be an (2, L) − double fuzzifying topological space. We define the maps
be an (2, L) − double fuzzifying topological space. We define the maps 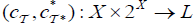 as follows
as follows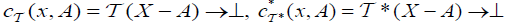 Then the pair
Then the pair 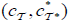 is an M-double fuzzy contiguity relation on X induces by (2, L) − double fuzzifying topological space
is an M-double fuzzy contiguity relation on X induces by (2, L) − double fuzzifying topological space 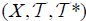 . Let (c,c*) be an M-double fuzzy contiguity relation on X. Define
. Let (c,c*) be an M-double fuzzy contiguity relation on X. Define 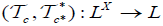 as follows:
as follows: 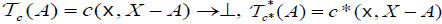 . Then
. Then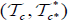 is an (2, L) − double fuzzifying topological space on X induces by an M-double fuzzy contiguity relation on X. Furthermore
is an (2, L) − double fuzzifying topological space on X induces by an M-double fuzzy contiguity relation on X. Furthermore 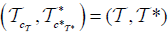 and
and 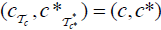 .
.
Proof
(A)(DC1) For each A ∈LX, 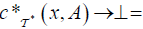
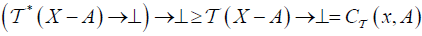 ,
,
(DC2) For each A, B∈LX ,
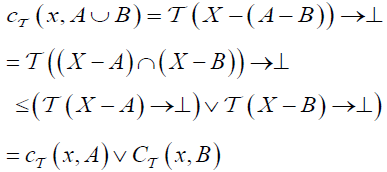
and
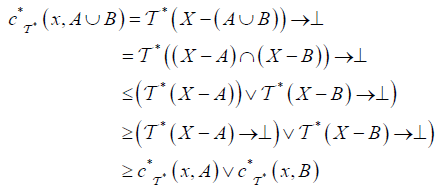
(DC3) For 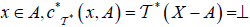 and
and 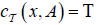
(DC4)
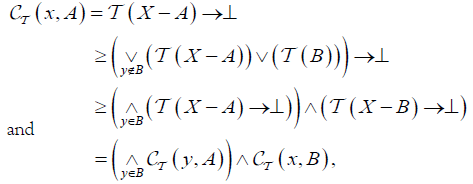
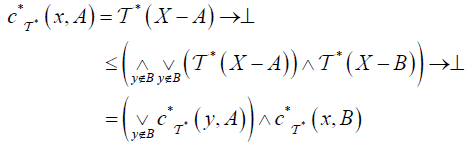
(B)
(DOI) for every x∈X and A ∈2X, 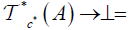
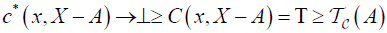
(DO2) 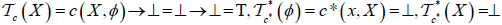
(DO3)
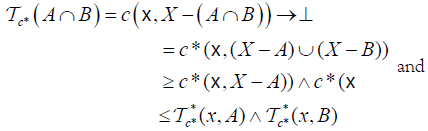
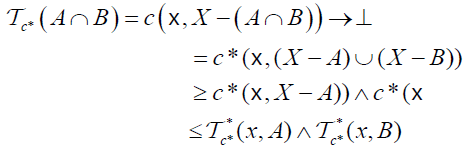 ,
,
(DO4)
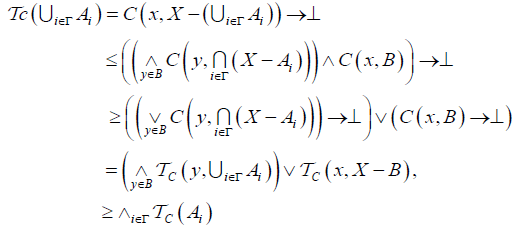
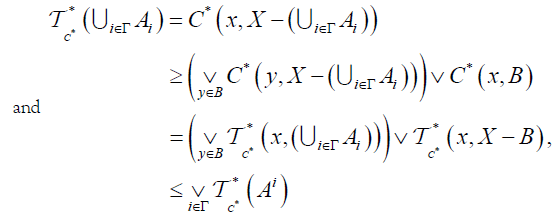
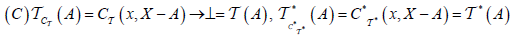
And 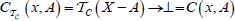 and
and 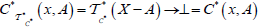
Theorem 4.3
Let 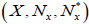 and be an (2, L) double fuzzifying neighborhood system of x. We define the maps
and be an (2, L) double fuzzifying neighborhood system of x. We define the maps 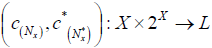 as follows:
as follows:
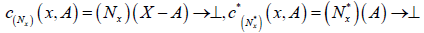 Then the pair
Then the pair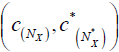 is anM-double fuzzy contiguity relation on X induces by (2, L) double fuzzifying
is anM-double fuzzy contiguity relation on X induces by (2, L) double fuzzifying 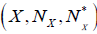 . Let (c,c* )be an M-double fuzzy contiguity relation on X. Define
. Let (c,c* )be an M-double fuzzy contiguity relation on X. Define 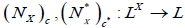 as follows:
as follows: 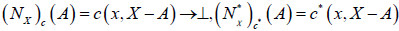 Then
Then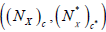 is an (2, L) -double fuzzifying neighborhood system induces by an M-double fuzzy contiguity relation on X. Furthermore
is an (2, L) -double fuzzifying neighborhood system induces by an M-double fuzzy contiguity relation on X. Furthermore 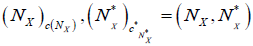 and
and 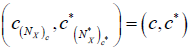 .
.
Proof (A)
(DC1) For each A∈2X, whenever
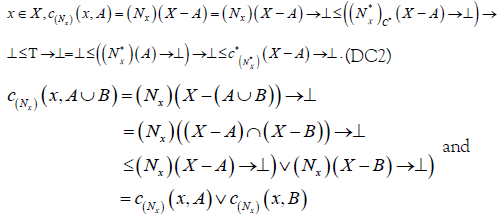
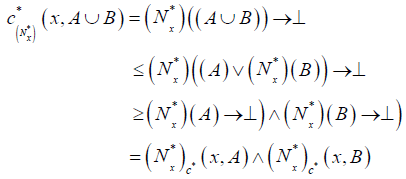
(DC3) whenever x∈ A,
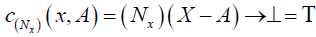 , and
, and 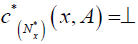 (DC4) ∀B∈P( X ),
(DC4) ∀B∈P( X ),
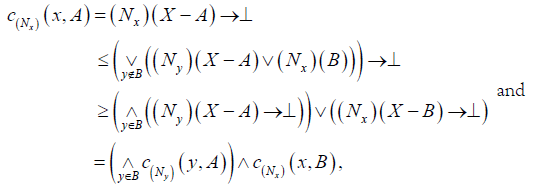
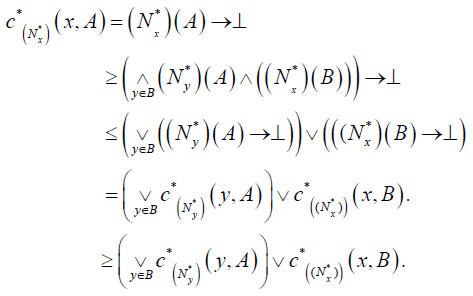
(B)
(DN − f1) forever x∈ X and
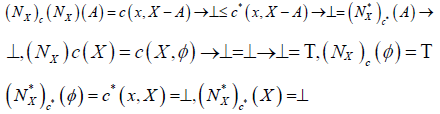
(DN − f2)
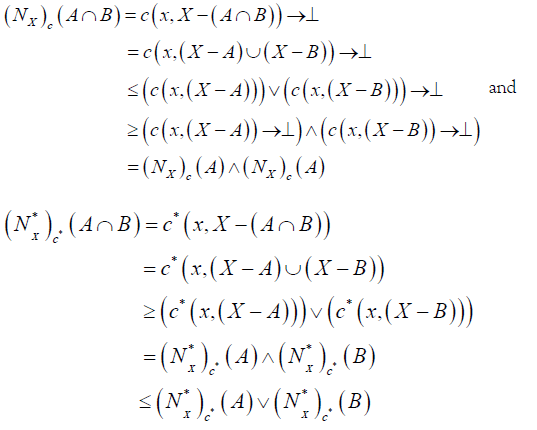
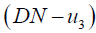 whenever x∉ A,
whenever x∉ A,
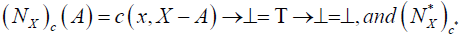
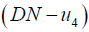 For each x∈ A, and A, B∈2X
For each x∈ A, and A, B∈2X
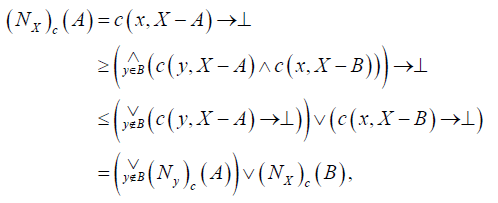
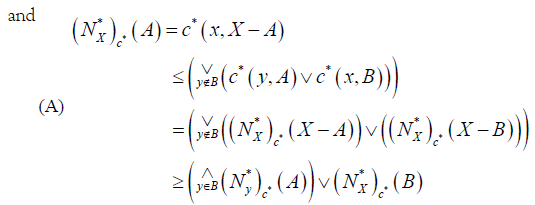
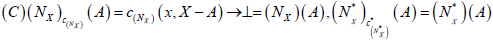 and
and 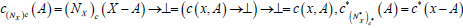 .
.
Definition 3.3. Let X be a nonempty set. A map 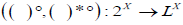 is called an (2, L) -double fuzzifying interior operator if (( )°, ( )*°) satisfies the following conditions:
is called an (2, L) -double fuzzifying interior operator if (( )°, ( )*°) satisfies the following conditions:
(1°)( A)° = ( A)*°→⊥ and ( X )° = Τ,(φ )*° =⊥
(2°)( A∩B)° = ( A)°∧(B)°, ( A∩B)*° = ( A)*°∨ (B)*°,
(3°)( A)° ≤ A, A ≤ ( A)*°,
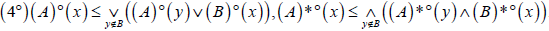 .
.
Theorem 4.4
Let 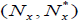 be an (2,M)-double fuzzifying neighborhood system of x. We Define
be an (2,M)-double fuzzifying neighborhood system of x. We Define 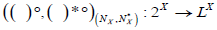 as follows:
as follows:
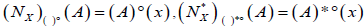 . Then
. Then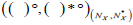 is an M-double fuzzifying interior operator induces by (2,M)-double fuzzifying neighborhood system of x. Let (( )°, ( )*°) be an M-double fuzzifying interior operator.
is an M-double fuzzifying interior operator induces by (2,M)-double fuzzifying neighborhood system of x. Let (( )°, ( )*°) be an M-double fuzzifying interior operator.
We Define 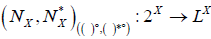 as
as
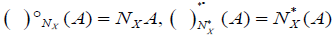 .
.
Then 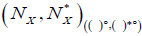 is an ( 2,M)-double fuzzifying neighborhood systemof x induces by M-double fuzzifying interior operator (( )°, ( )*°) on X. Moreover
is an ( 2,M)-double fuzzifying neighborhood systemof x induces by M-double fuzzifying interior operator (( )°, ( )*°) on X. Moreover 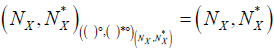 and
and 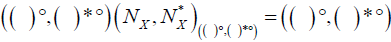 .
.
Proof
(A) For each A∈2X, 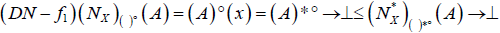 . And,
. And, 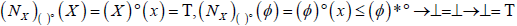 and
and 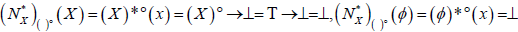 , (DN − f2) for each A, B∈2X
, (DN − f2) for each A, B∈2X
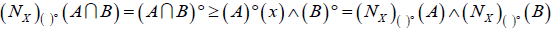 and
and 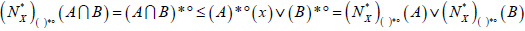
(DN − u3) whenever
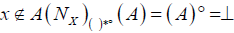 and
and 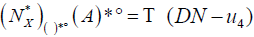 for each x∈ A,
for each x∈ A,
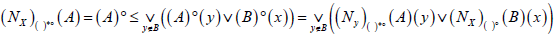
And 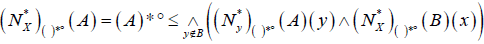
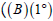 for each
for each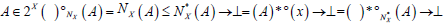 and
and 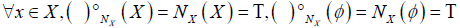 and
and 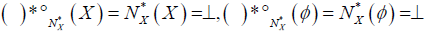
(2°) for each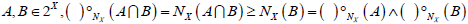 . and
. and 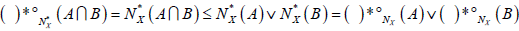 .
.
(3°) 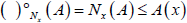 and
and 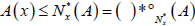 whenever x∉ A.
whenever x∉ A.
(4°) For each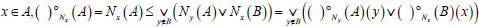 and
and 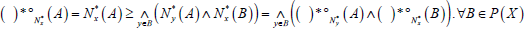 .
.
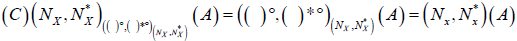 , and
, and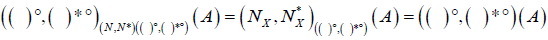 .
.
REFERENCES
- Höhle U. Upper semicontinuous fuzzy sets and applications. J Math Anal Appl. 1980;78:449-472.
- Höhle U. Characterization of L-topologies by L-valued neighborhoods. The Handbooks of Fuzzy Sets Series. Springer, Boston. 1999:389-432.
- Ying MS. A new approach for fuzzy topology (I), Fuzzy Sets and Systems. 1991;39:303-321.
- Ying MS. A new approach for fuzzy topology (II), Fuzzy Sets and Systems. 1992;47:221-232.
- Ying MS. A new approach for fuzzy topology (III), Fuzzy Sets and Systems. 1993;55:192-207.
- Fan L. A new approach to quantitative domain theory, Electronic Notes in Theoretic Computer Sci. 2001;24:77-87.
- Fang J. I-FTOP is isomorphic to I-FQN and I-AITOP. Fuzzy Sets and Systems. 2002;147:317-325.
- Fang J. Sums of L- fuzzy topological spaces. Fuzzy Sets and Systems. 2004;157:739-754.
- Höhle U. Commutative, residuated l-monoids, Non-Classical Logics and their Applications to Fuzzy Sub-sets. Springer, Dordrecht. 1995:53-106.
- Rodabaugh SE, Klement EP. Topological And Algebraic Structures in Fuzzy Sets: A Handbook of Recent Developments in the Mathematics of Fuzzy Sets, Springer.
- Zahran AM, Khalaf MM. On semi separation axioms in L-fuzzifying bitopological space. J Egyptian Mathematical Society. 2016;24:609-616.
- Ramadan AA, El-latif AA. Categories isomorphic to (L,M)- DFTOP. J Egyptian Mathematical Society. 2016; 24:499-507.
- Pavelka J. On fuzzy logic II. Z. Math. Logic Gvundlagen Math. 1979;24:119-122.
- Chattopadhyay KC, Hazra RN, Samanta SK. Gradation of openness: Fuzzy topology. Fuzzy Sets and Systems. 1992; 49:237-242.
- Coker D. An introduction of Double fuzzy topological spaces. Fuzzy Sets and Systems. 1997; 88:81-89.






